0% found this document useful (0 votes)
8 views3 pagesIntro To Sampling Theorem - Engr Chris
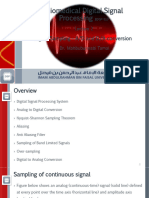
The document explains the process of sampling, which converts continuous-time analog signals into discrete-time digital signals by measuring the signal at specific intervals. It introduces the Sampling Theorem, which states that to accurately reproduce a signal, it must be sampled at a frequency greater than twice its maximum frequency, known as the Nyquist rate. Additionally, it discusses the phenomenon of aliasing that occurs when a signal is sampled below the Nyquist rate, leading to distortion and the introduction of non-existent frequency components.
Uploaded by
peterhabibadamiCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
8 views3 pagesIntro To Sampling Theorem - Engr Chris
The document explains the process of sampling, which converts continuous-time analog signals into discrete-time digital signals by measuring the signal at specific intervals. It introduces the Sampling Theorem, which states that to accurately reproduce a signal, it must be sampled at a frequency greater than twice its maximum frequency, known as the Nyquist rate. Additionally, it discusses the phenomenon of aliasing that occurs when a signal is sampled below the Nyquist rate, leading to distortion and the introduction of non-existent frequency components.
Uploaded by
peterhabibadamiCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 3