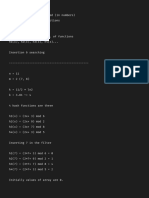
M.
Sc Data Science and Artificial Intelligence Module II
1. Compute the minhash for each column if we use the following three hash functions:
(h1) = 3x+3 mod 5, (h2) = x+2 mod 5, (h3) = 4x+1 mod 5.
Row S1 S2 S3 S4
0 1 0 0 1
1 0 0 1 0
2 0 1 0 1
3 1 0 1 1
4 0 0 1 0
2. Stream: 7, 12, 7, 5, 18, 41, 26, 12, 33, 64, 18, 5, 72
Hash: h(x)=(5x+1) mod 32 and h(x)=(7x+3)mod32
Count the number of distinct element using flajolet and martin algorithm.
3. Q-2 Given stream: 2 3 7 1 5 8 5 7 9 6 4 4 5 6 5 8 8 5 2 2 2 1 1 6 7. Find its surprise number
using AMS algorithm. Assume values of x1, x2, x3 and x4 as 1, 3, 5 and 10.
4. Consider the bit array B=13 bits and hash function
h1(x) = x+1 mod 13
h2(x) = (2x + 5) mod 13
add in the bloom filter following numbers:
8, 17, 25, 9, 20.
Given integer 7 and 5, use the bloom filter to check whether it is contained in
S, and give reason.
5. A Bloom filter is designed to store 1000 elements and has 12000 bits. What is the
optimal number of hash functions k to minimize the false positive probability?
6. Explain the DGIM algorithm for counting 1s. Given stream and buckets as per DGIM
algorithm with window size 40:
65 80 87 92 95 98 100
1001010110001011 10101010101011 1010101 101 11 1 1
Estimate the number of 1’s in above stream: (i) k=25 (ii) k=15 (iii) k=8
7. Given stream and buckets as per DGIM algorithm with window size 40:
65 80 87 92 95 98 100
1001010110001011 10101010101011 1010101 101 11 1 1
Assume following bit arrive in the window
001110110
Update the window as per DGIM.