0% found this document useful (0 votes)
416 views31 pagesDCS - Sampling and Quantization
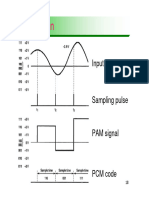
The document discusses various methods of pulse modulation used in analog and digital communication systems. It describes pulse amplitude modulation (PAM), pulse width modulation (PWM), and pulse position modulation (PPM) as analog pulse modulation techniques. For digital pulse modulation, it covers pulse code modulation (PCM) and delta modulation (DM). The key steps of PCM include sampling the analog signal, quantizing the samples into discrete levels, and encoding the quantized samples into binary codewords for transmission.
Uploaded by
Ahsan FawadCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPT, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
416 views31 pagesDCS - Sampling and Quantization
The document discusses various methods of pulse modulation used in analog and digital communication systems. It describes pulse amplitude modulation (PAM), pulse width modulation (PWM), and pulse position modulation (PPM) as analog pulse modulation techniques. For digital pulse modulation, it covers pulse code modulation (PCM) and delta modulation (DM). The key steps of PCM include sampling the analog signal, quantizing the samples into discrete levels, and encoding the quantized samples into binary codewords for transmission.
Uploaded by
Ahsan FawadCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPT, PDF, TXT or read online on Scribd
/ 31