0% found this document useful (0 votes)
451 views42 pagesLecture 3 - Design For Static Loading
The document discusses various topics related to mechanical loading and design for static loading, including:
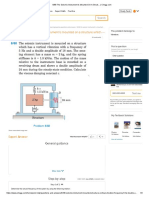
- Types of mechanical loading like axial, transverse, and shear loads
- Types of mechanical stresses like direct, indirect, and compound stresses
- Thermal stresses generated due to constraints on thermal expansion
- Ductile to brittle transition temperature and how it relates to material behavior
- Stress concentration factor and how it accounts for stress variations due to discontinuities
- Principal planes and stresses in three-dimensional stress elements
- Mohr's circle and how it relates normal and shear stresses on different planes
- Numerical examples on stress analysis and failure theories
Uploaded by
M Shoaib AkramCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
451 views42 pagesLecture 3 - Design For Static Loading
The document discusses various topics related to mechanical loading and design for static loading, including:
- Types of mechanical loading like axial, transverse, and shear loads
- Types of mechanical stresses like direct, indirect, and compound stresses
- Thermal stresses generated due to constraints on thermal expansion
- Ductile to brittle transition temperature and how it relates to material behavior
- Stress concentration factor and how it accounts for stress variations due to discontinuities
- Principal planes and stresses in three-dimensional stress elements
- Mohr's circle and how it relates normal and shear stresses on different planes
- Numerical examples on stress analysis and failure theories
Uploaded by
M Shoaib AkramCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
/ 42