0% found this document useful (0 votes)
70 views22 pagesNumerical Integratio N: Prepared By: Engr. Cielito V. Maligalig
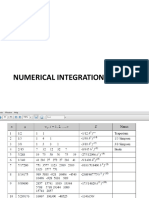
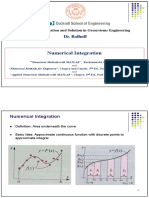
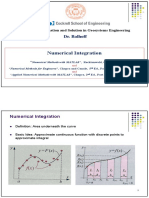
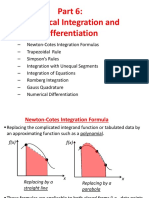
This document discusses numerical integration techniques including the trapezoidal rule, Simpson's 1/3 rule, and Simpson's 3/8 rule. It provides the formulas for each method and explains how to derive them. An example problem is shown calculating the integral of xsinx from 0.5 to 1.2 using each technique. The document concludes with an assignment to use these numerical integration methods with Excel to approximate integrals.
Uploaded by
Craeven AranillaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
70 views22 pagesNumerical Integratio N: Prepared By: Engr. Cielito V. Maligalig
This document discusses numerical integration techniques including the trapezoidal rule, Simpson's 1/3 rule, and Simpson's 3/8 rule. It provides the formulas for each method and explains how to derive them. An example problem is shown calculating the integral of xsinx from 0.5 to 1.2 using each technique. The document concludes with an assignment to use these numerical integration methods with Excel to approximate integrals.
Uploaded by
Craeven AranillaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
/ 22