0% found this document useful (0 votes)
94 views24 pagesRational and Exponential Functions
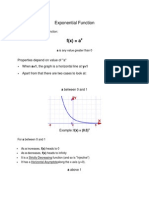
Here are the steps to find the rule for the exponential function given the initial value of 3 and the point (1,4):
1) The initial value (y-intercept) is 3, so the general form is y = 3(base)x
2) A point on the graph is (1,4)
3) Plug the point into the general form:
4 = 3(base)1
4) Divide both sides by 3:
4/3 = base
5) Take the square root of both sides:
(4/3)1/2 = base
Therefore, the rule is y = 3(√4/3)x
Validate by
Uploaded by
MissConnellCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
94 views24 pagesRational and Exponential Functions
Here are the steps to find the rule for the exponential function given the initial value of 3 and the point (1,4):
1) The initial value (y-intercept) is 3, so the general form is y = 3(base)x
2) A point on the graph is (1,4)
3) Plug the point into the general form:
4 = 3(base)1
4) Divide both sides by 3:
4/3 = base
5) Take the square root of both sides:
(4/3)1/2 = base
Therefore, the rule is y = 3(√4/3)x
Validate by
Uploaded by
MissConnellCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
/ 24