0% found this document useful (0 votes)
64 views15 pagesTransformation Parent Functions
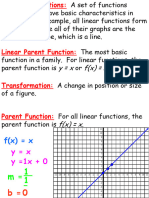
The document discusses parent functions and transformations of functions. It defines parent functions as basic algebraic functions like linear, quadratic, square root, exponential, rational, and logarithmic. Transformations of parent functions include vertical and horizontal shifts or stretches, reflections, and multiple transformations applied in a specific order. Function families are formed from transformations of a single parent function. Inverses and asymptotes are also discussed in relation to parent functions and their transformations.
Uploaded by
qqvhc2x2prCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
64 views15 pagesTransformation Parent Functions
The document discusses parent functions and transformations of functions. It defines parent functions as basic algebraic functions like linear, quadratic, square root, exponential, rational, and logarithmic. Transformations of parent functions include vertical and horizontal shifts or stretches, reflections, and multiple transformations applied in a specific order. Function families are formed from transformations of a single parent function. Inverses and asymptotes are also discussed in relation to parent functions and their transformations.
Uploaded by
qqvhc2x2prCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
/ 15