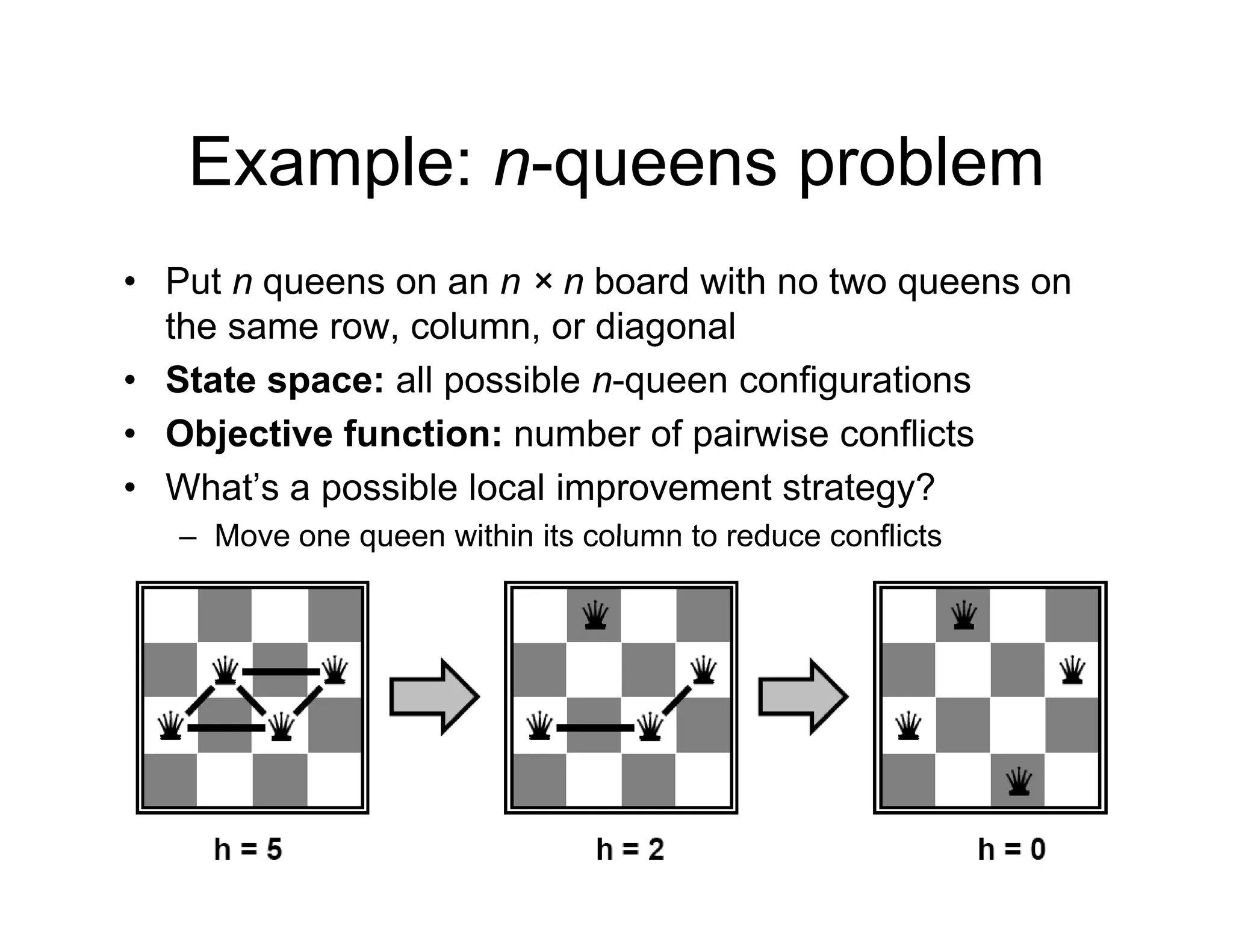
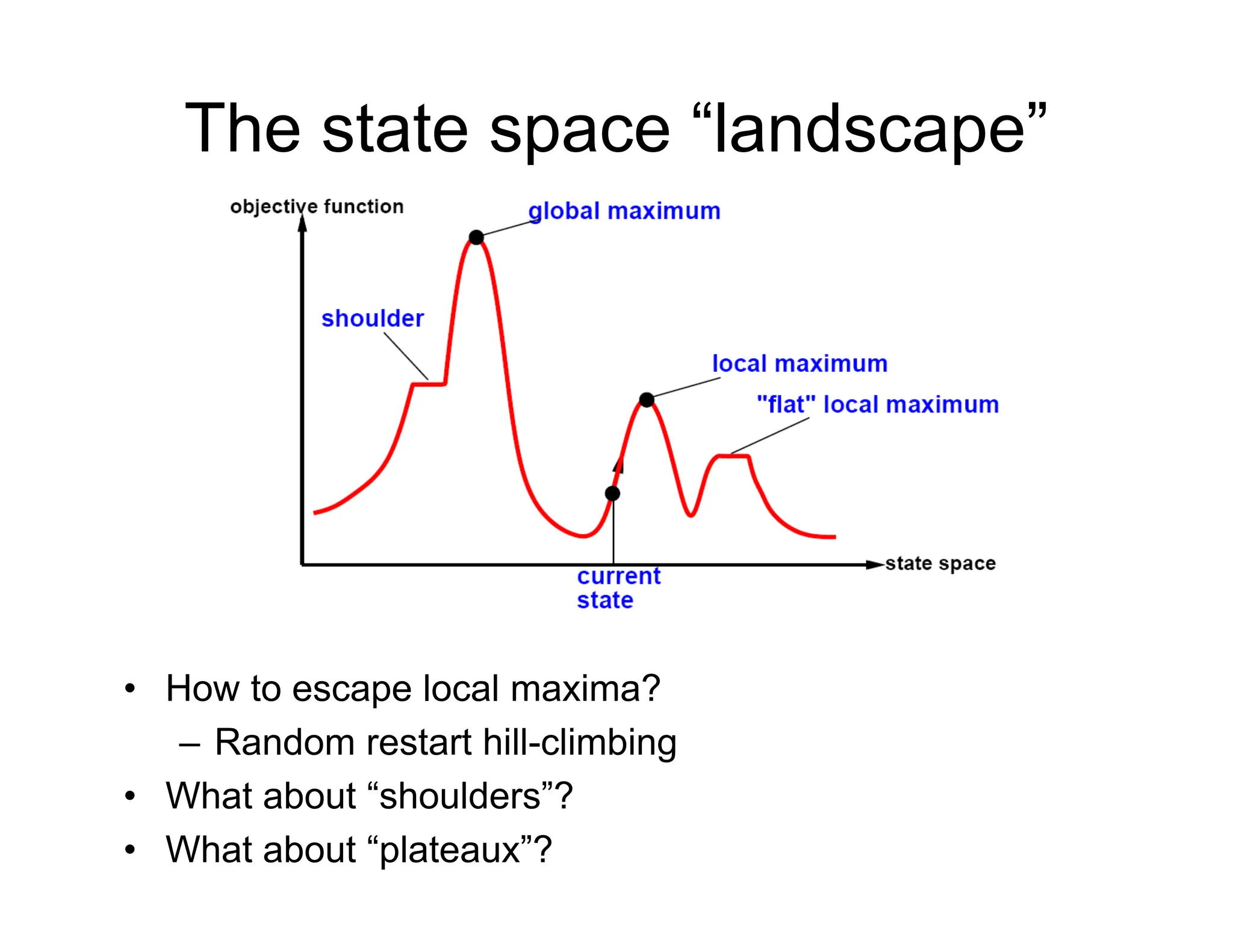
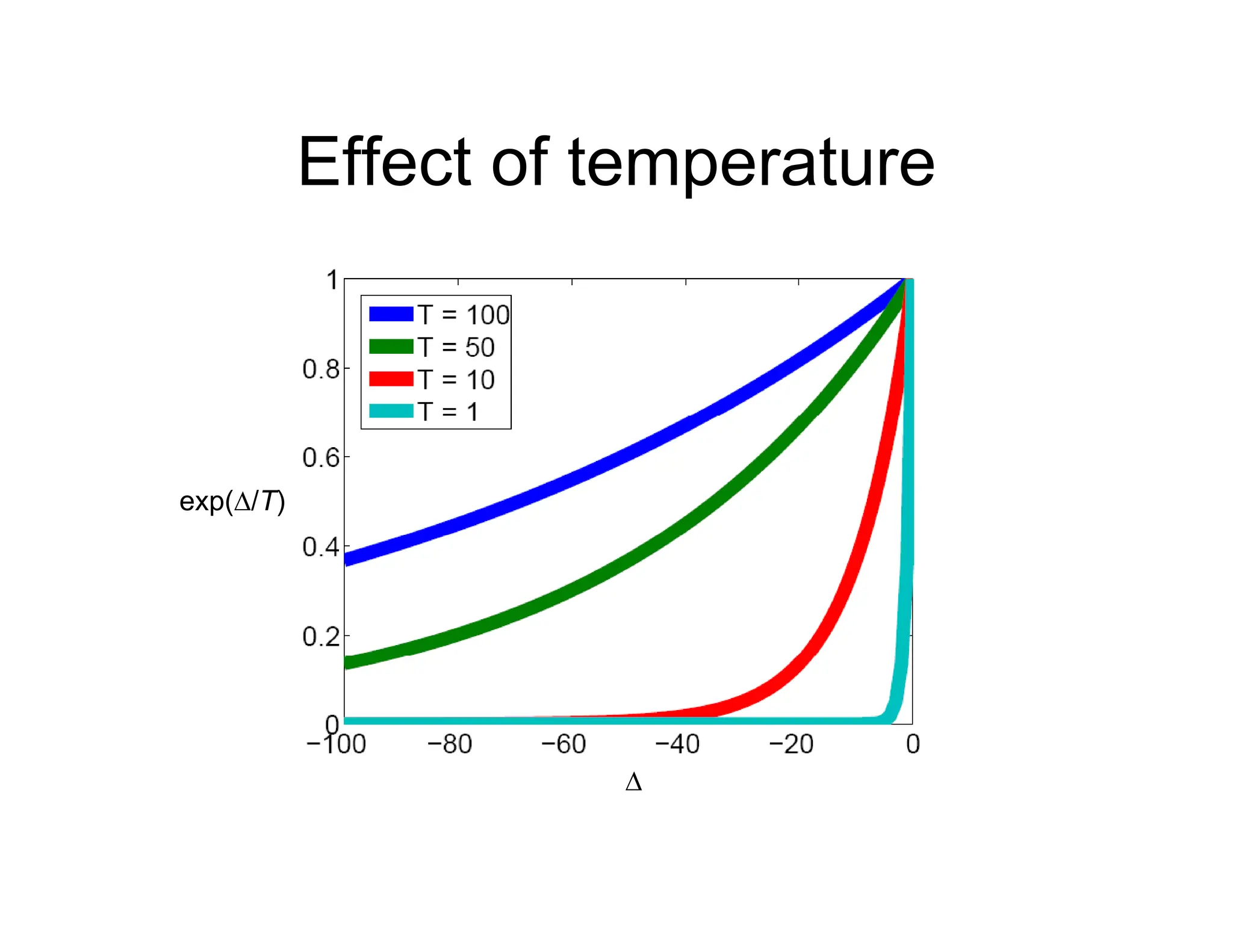
The document discusses local search algorithms used in optimization problems, focusing on the n-queens and traveling salesman problems as examples. It explains the concepts of state space, objective functions, and improvement strategies, detailing techniques like hill-climbing and simulated annealing. Additionally, it notes the challenges of local maxima and introduces alternative methods such as local beam search and Markov Chain Monte Carlo (MCMC) algorithms for exploring complex state spaces.