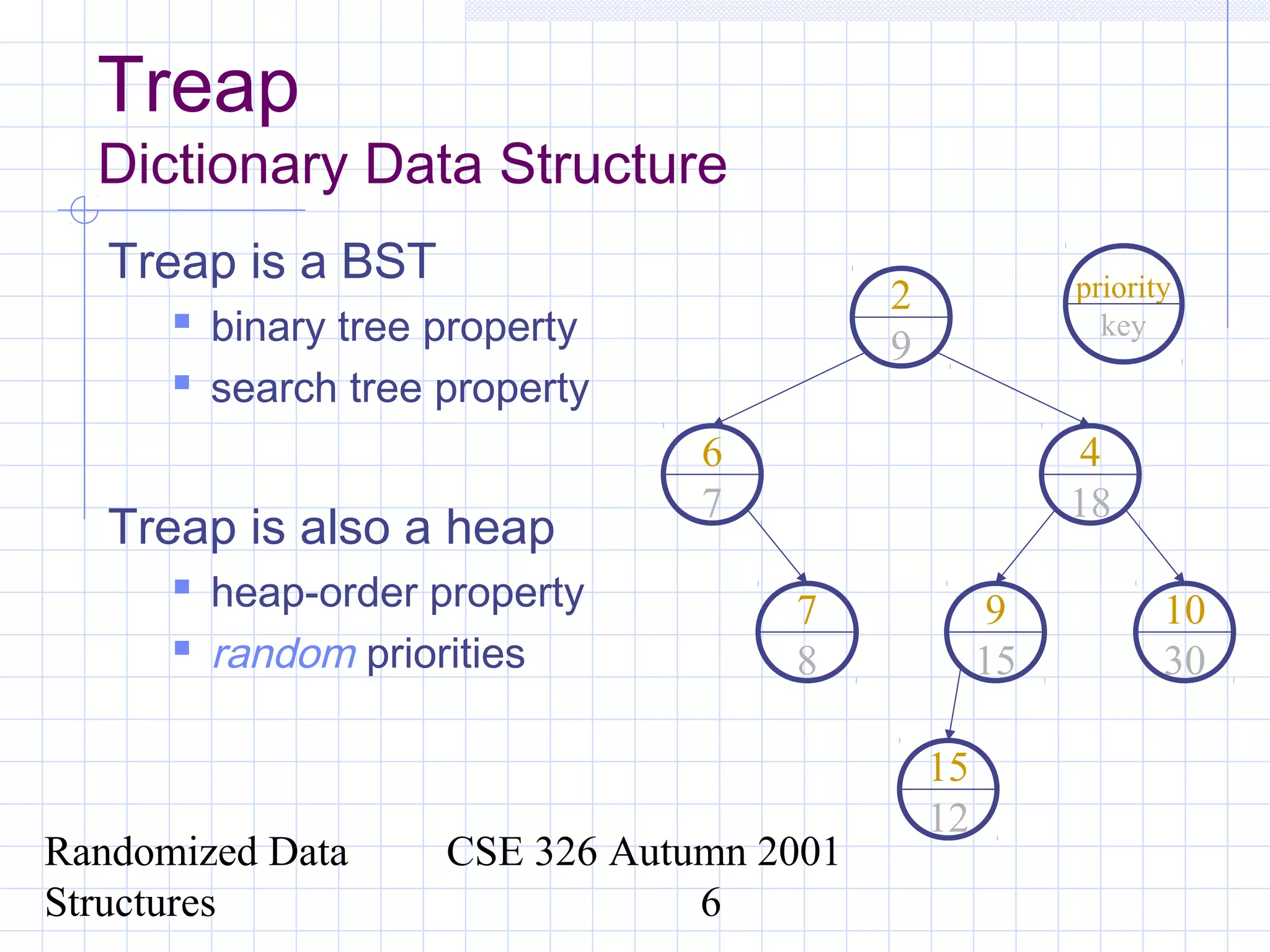
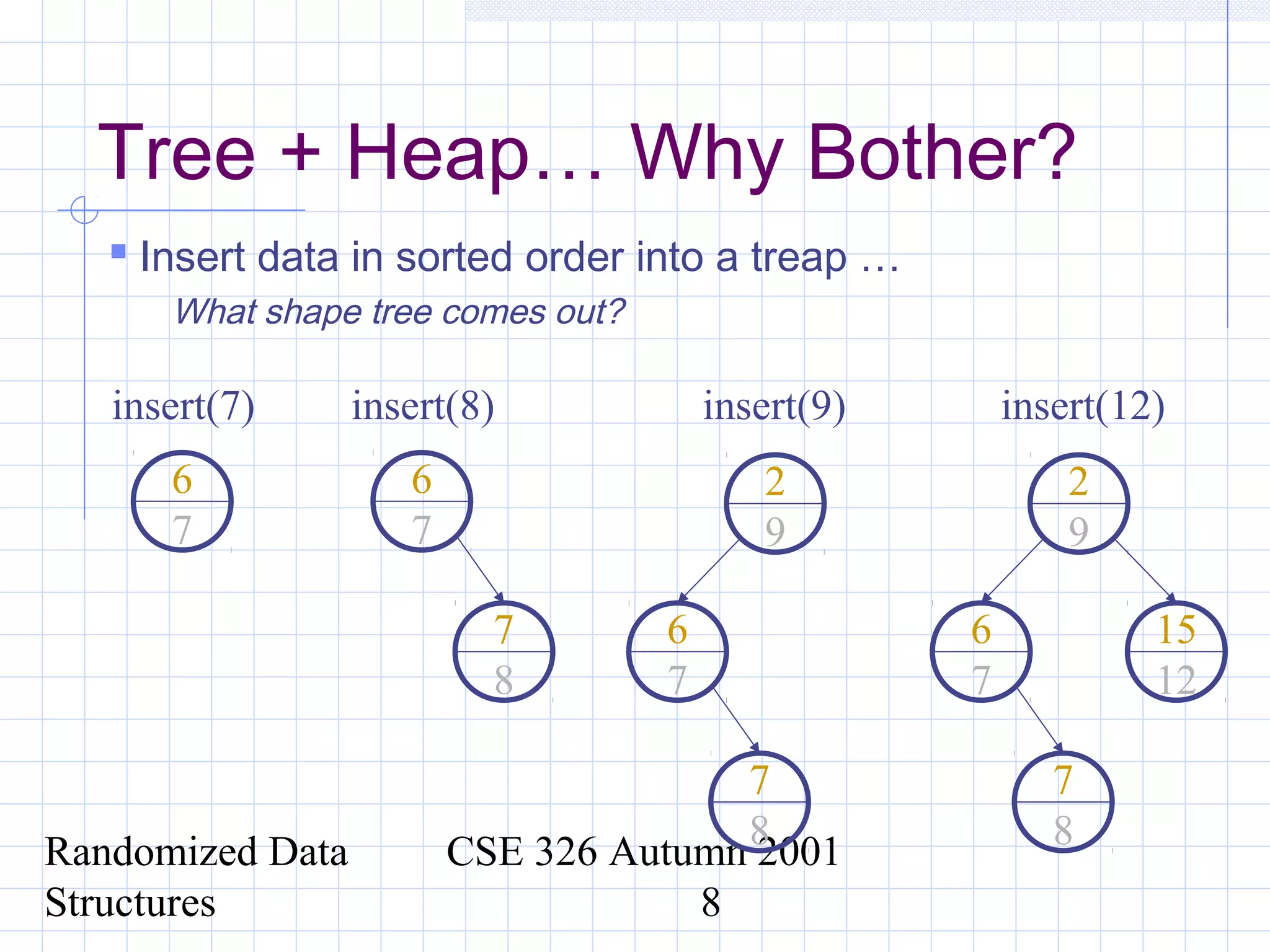
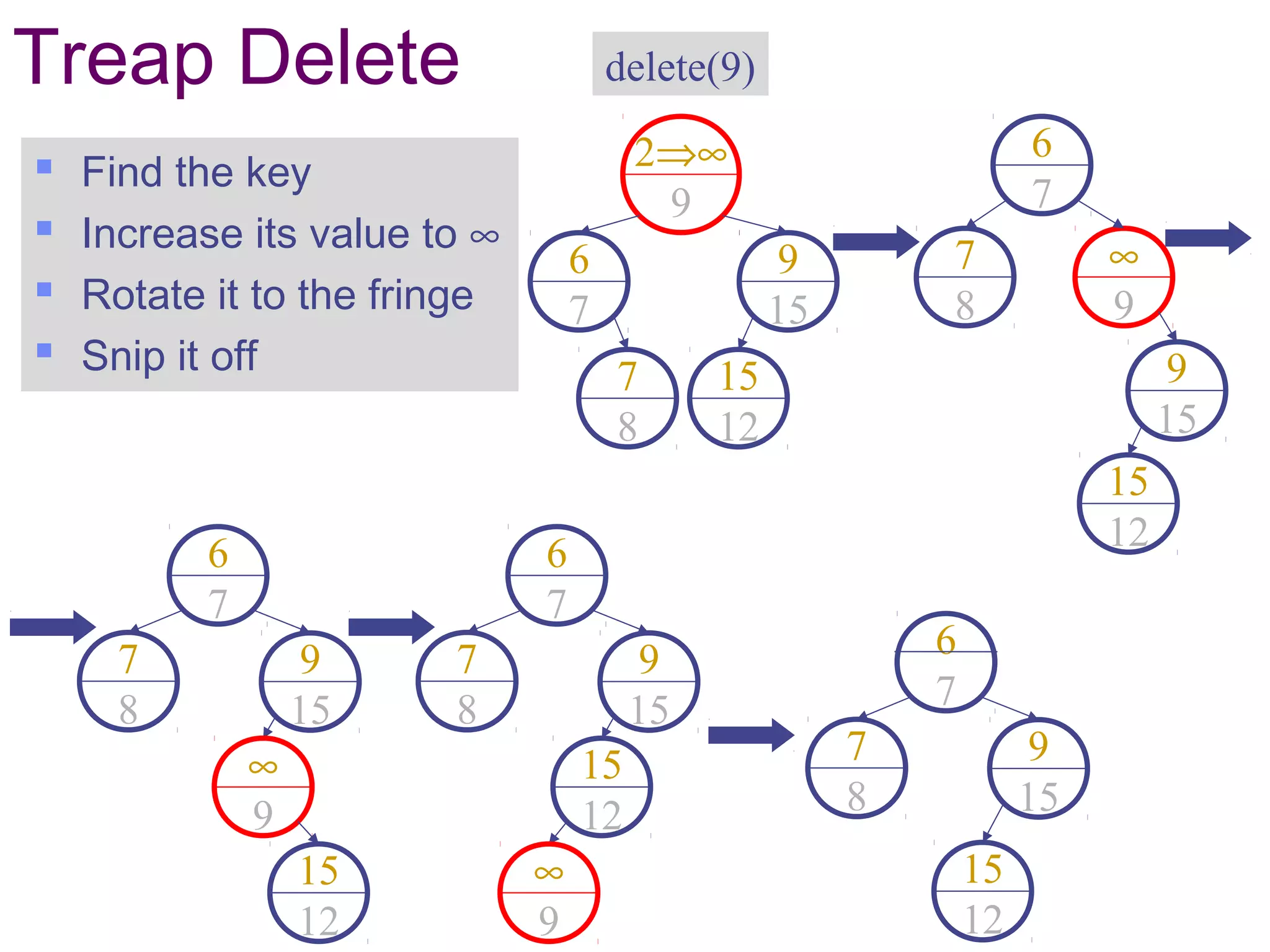
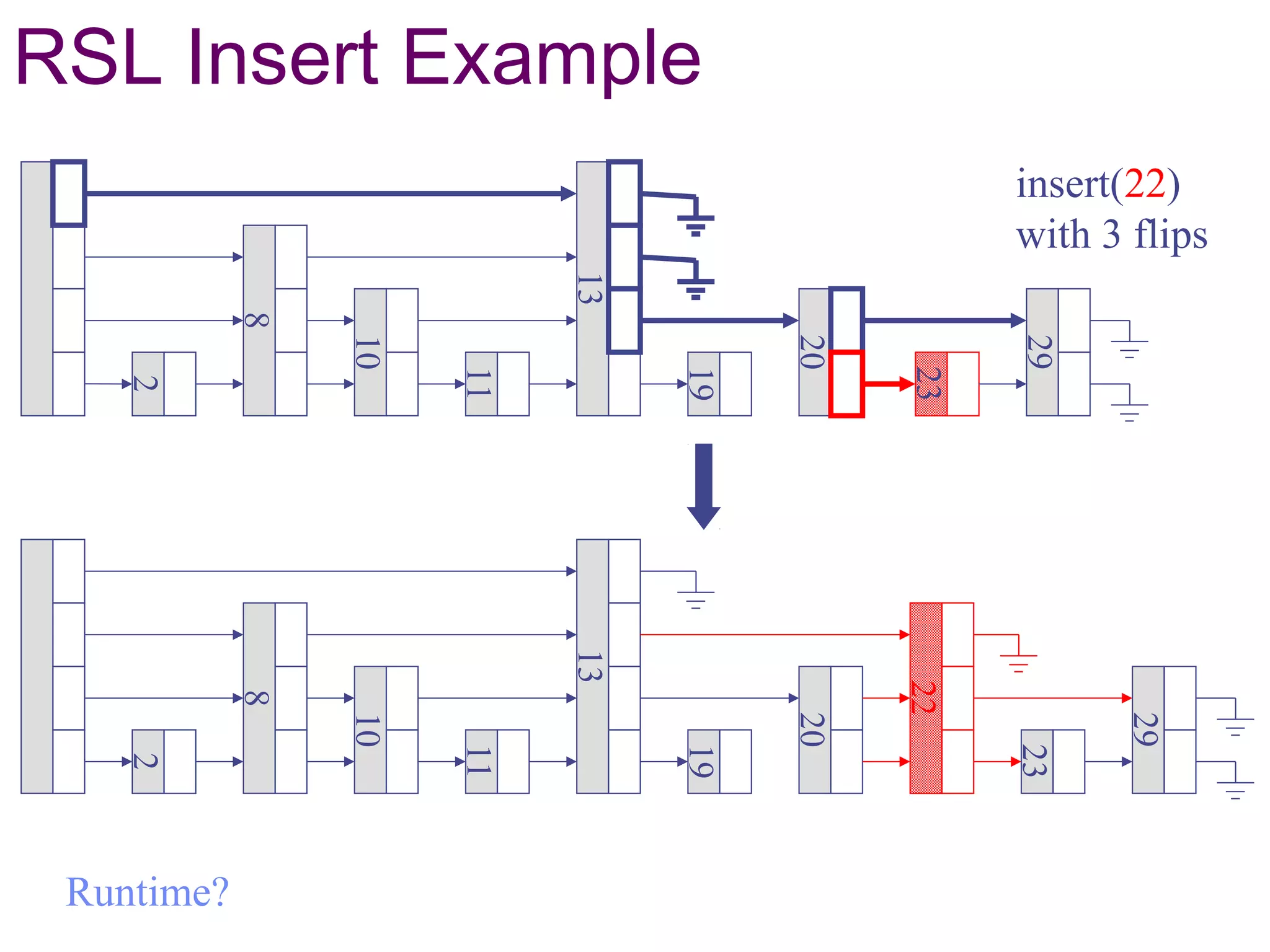
This document discusses randomized data structures and algorithms. It begins by motivating randomized data structures as a way to transform average case runtimes into expected runtimes that are not dependent on specific inputs. It then provides examples of randomized data structures like treaps and randomized skip lists that provide efficient operations like insertion, deletion, and search in expected logarithmic time. It also discusses how randomization can be applied in algorithms like primality testing.