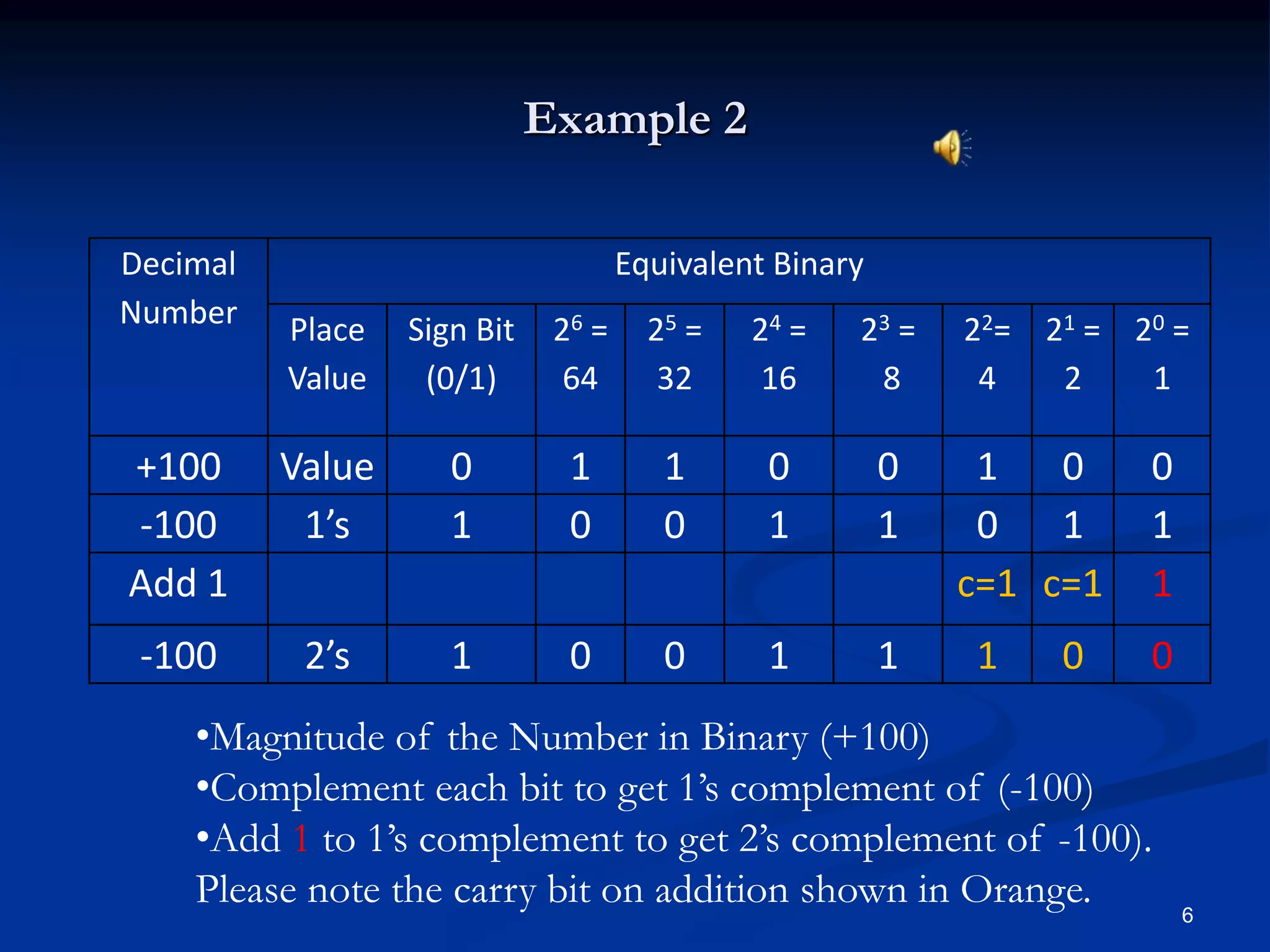
This document discusses binary arithmetic using 2's complement notation. It explains that 2's complement notation is an efficient method for binary addition and subtraction. Positive numbers are represented normally, while negative numbers have their bits complemented and 1 added. Several examples are provided of adding positive and negative numbers in binary using 2's complement notation. The document checks the reader's understanding with practice problems adding various positive and negative binary numbers and identifying if overflow occurs.