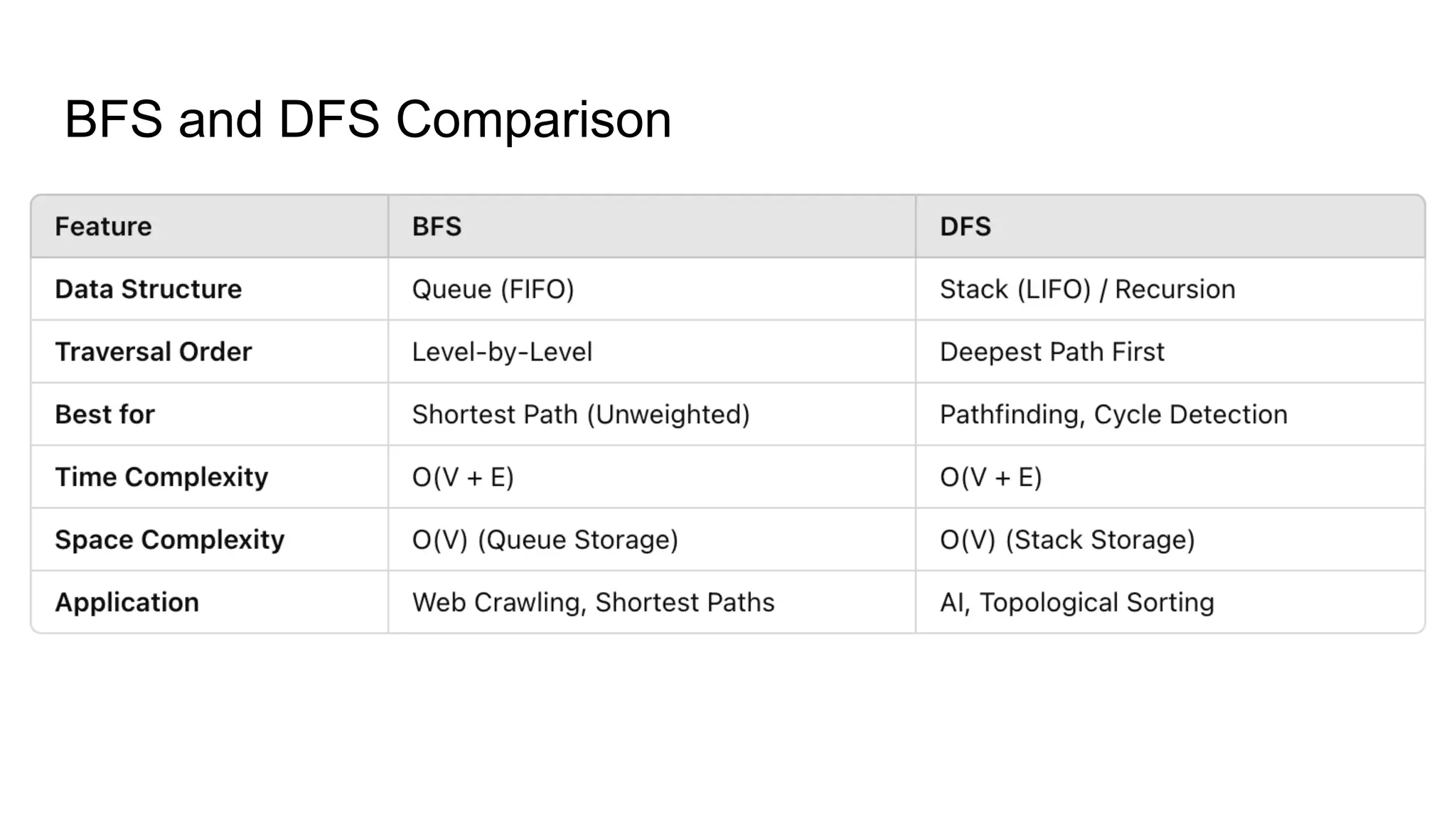
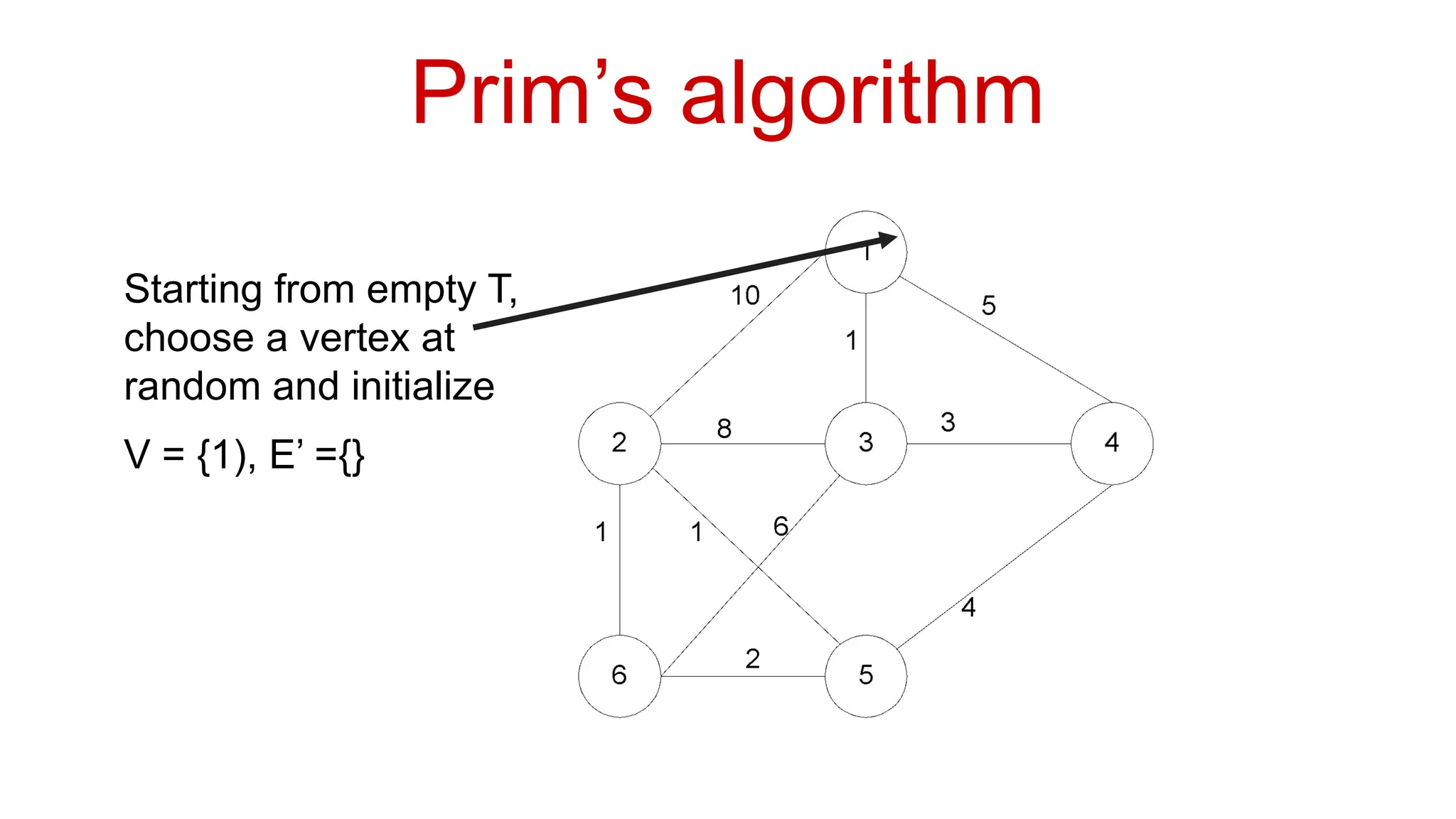
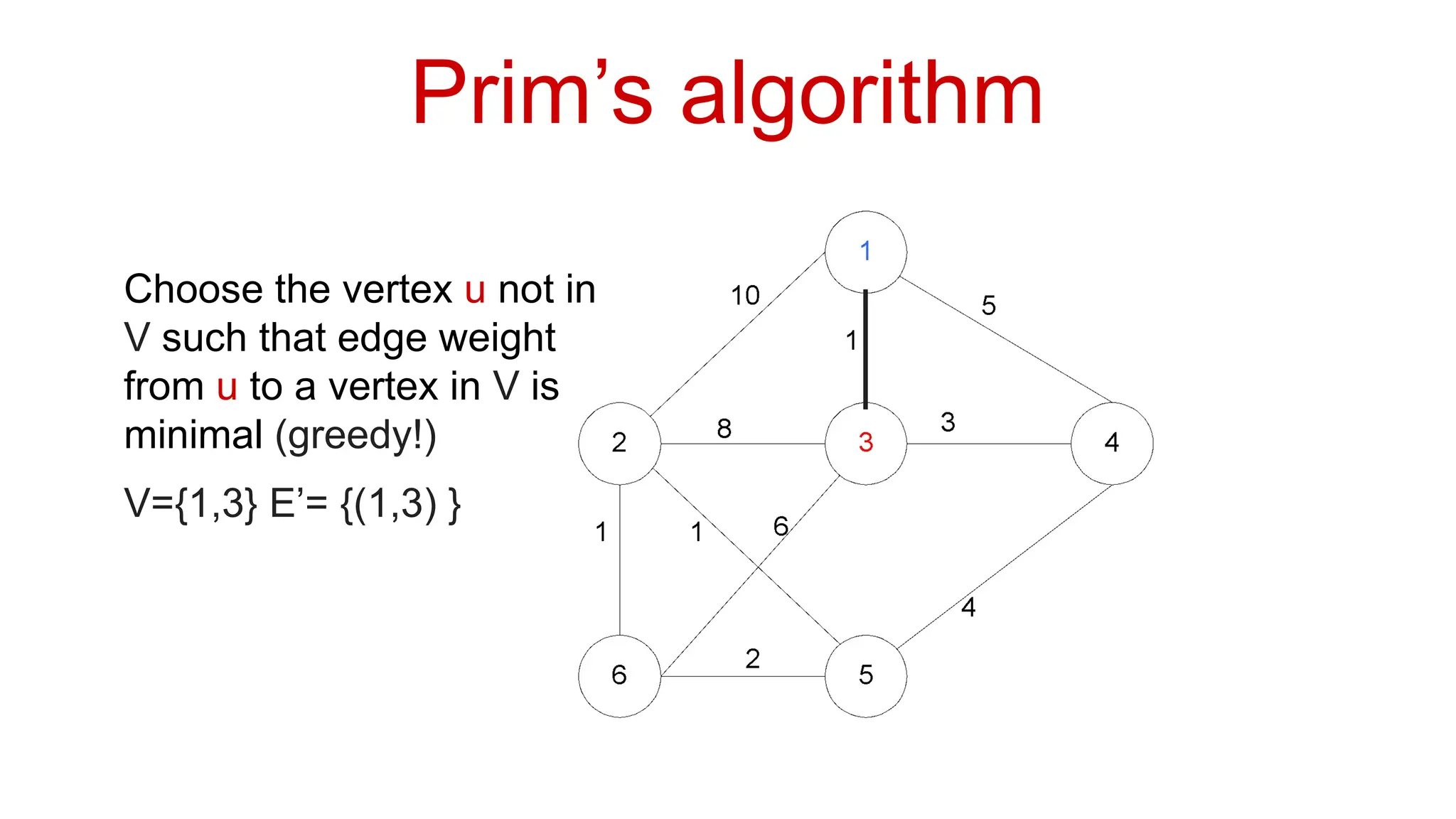
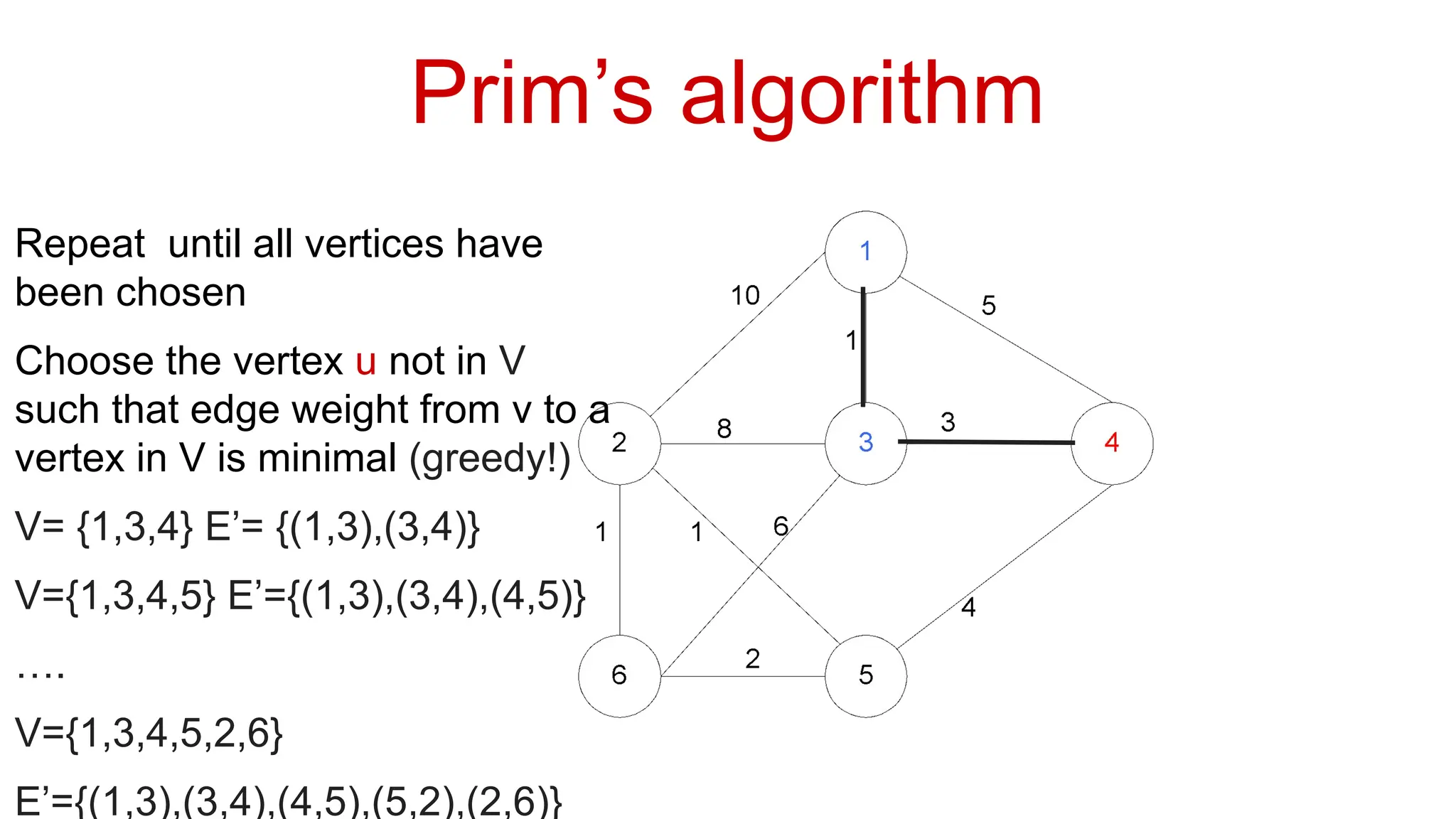
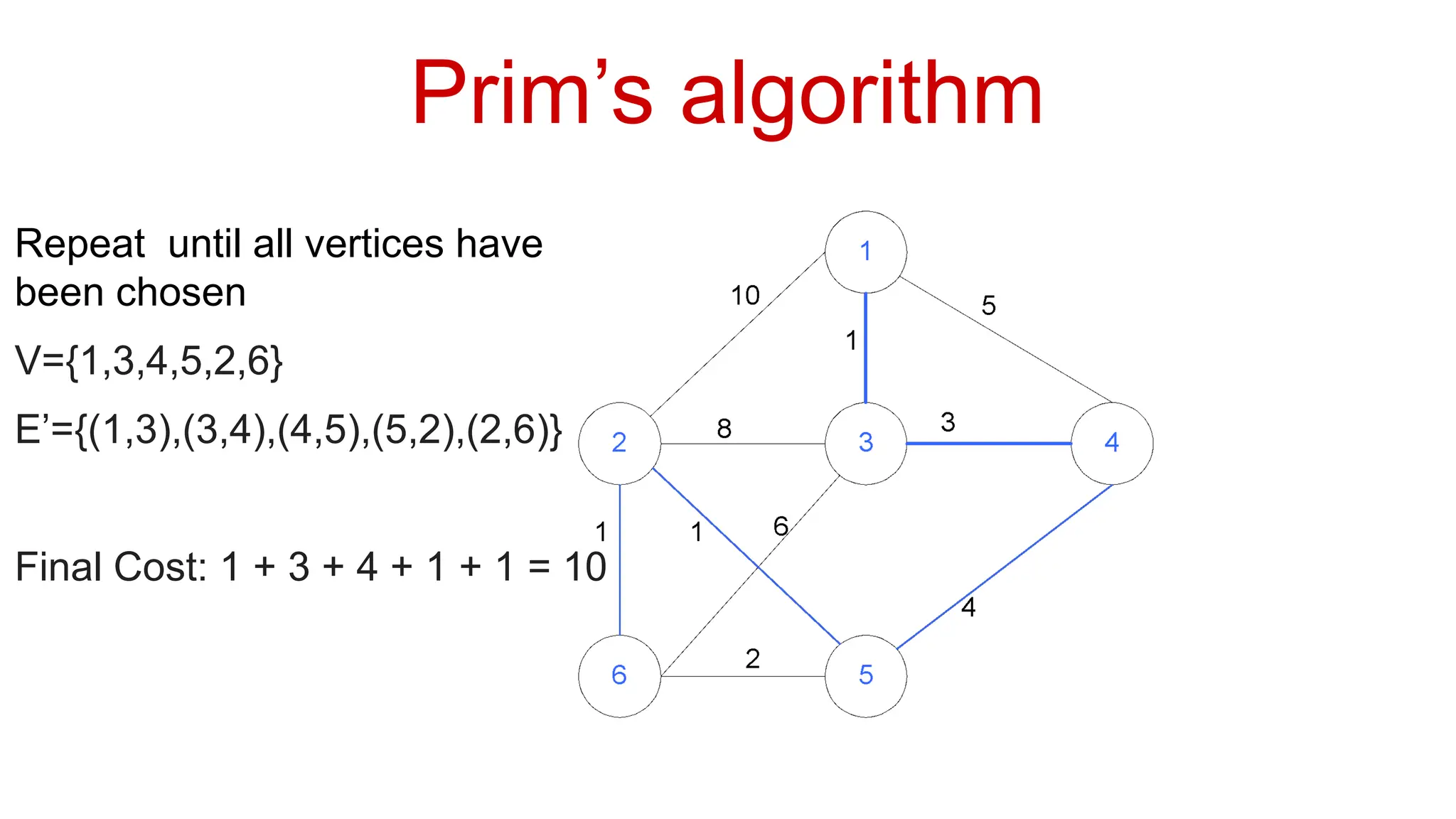
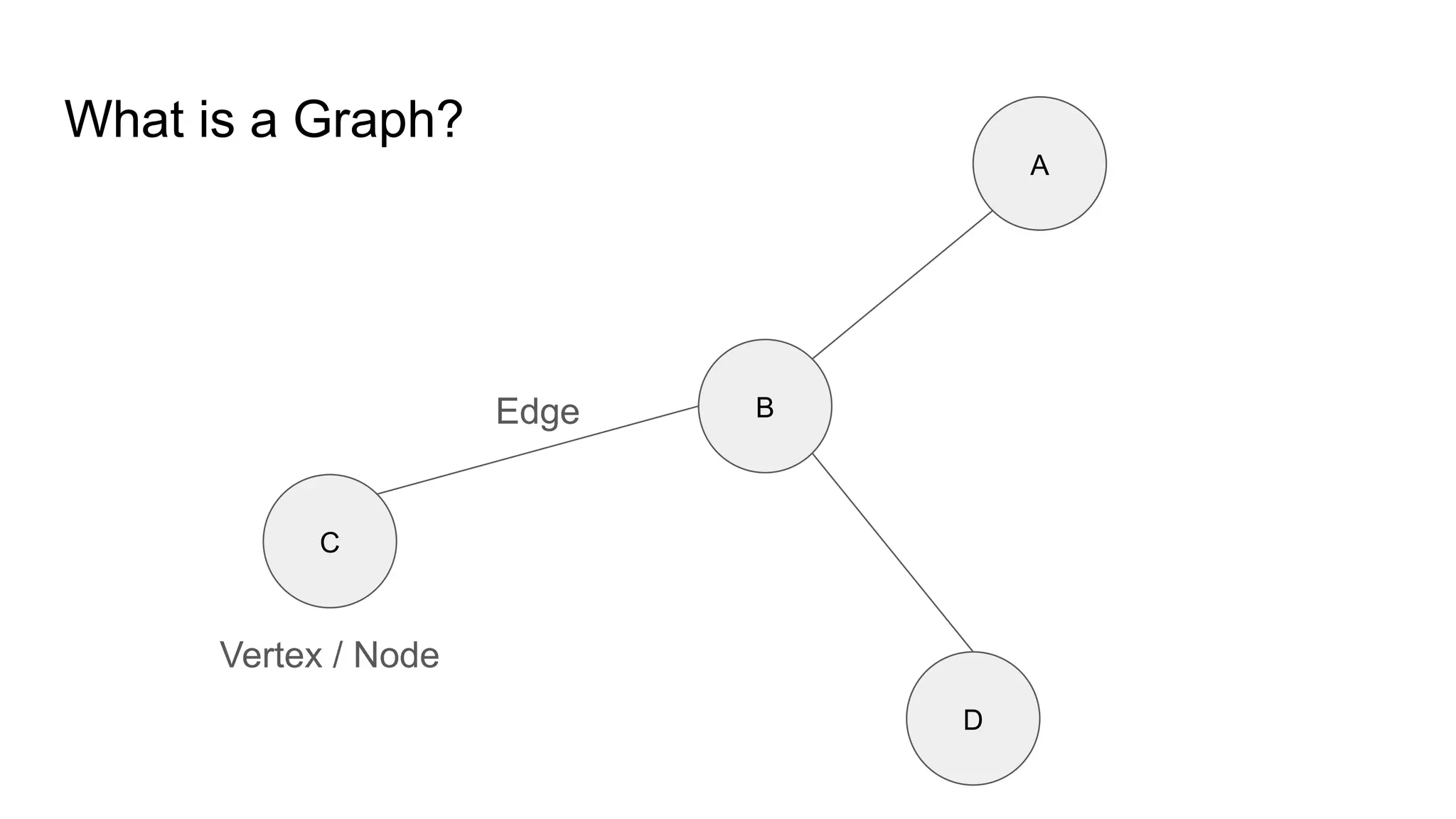
Basic Graph Algorithms Vertex (Node): lk

Basic Graph Algorithms
Naeemul Hassan

What is a Graph?
C
B
D
A
Vertex / Node
Edge

Why Graphs?
● Social Networks
○ Facebook, Twitter
● Transportation
○ Urban Design
○ UPS
● Web Graphs
○ Google PageRank
● Recommendation Systems
○ Netflix
● Knowledge Graph
○ Wikipedia
● Citation Networks
● Can you give another application of
Graphs?

Basic Definitions
Vertex (Node): A fundamental unit of a graph, representing an entity (e.g., a
person in a social network, a city in a transportation network).
Edge: A connection between two vertices, representing a relationship (e.g., a
friendship, a road between cities).
Neighbors: A set of vertices that are connected to a vertex.

Directed Graph (Digraph): A graph where edges have a direction, meaning (A →
B) is not the same as (B → A). Example: Twitter follows.
Graph Types
C
B
D
A

Undirected Graph: A graph where edges have no direction, meaning (A — B) is
the same as (B — A). Example: Facebook friendships.
Graph Types
C
B
D
A

Graph Types
Weighted Graph: A graph where each edge has an associated weight (or cost),
representing distance, time, or importance. Example: A road network with travel
distances.
C
B
D
A
5
2
3.5

Unweighted Graph: A graph where all edges are considered equal (weight is
implicitly 1). Example: A simple social network.
Graph Types
C
B
D
A

Probabilistic Graph: A graph where edges (and sometimes nodes) have associated
probabilities, representing uncertainty in connections. This type of graph is used to model
systems where relationships are not deterministic but occur with some likelihood.
Consider a social influence network where people have a probability of influencing their friends:
● Nodes: People in a network.
● Edges: Represent influence with a probability.
Example: Alice persuades Bob to watch a movie with 70% probability, while Bob persuades
Charlie with 50% probability.
Demo
Graph Types

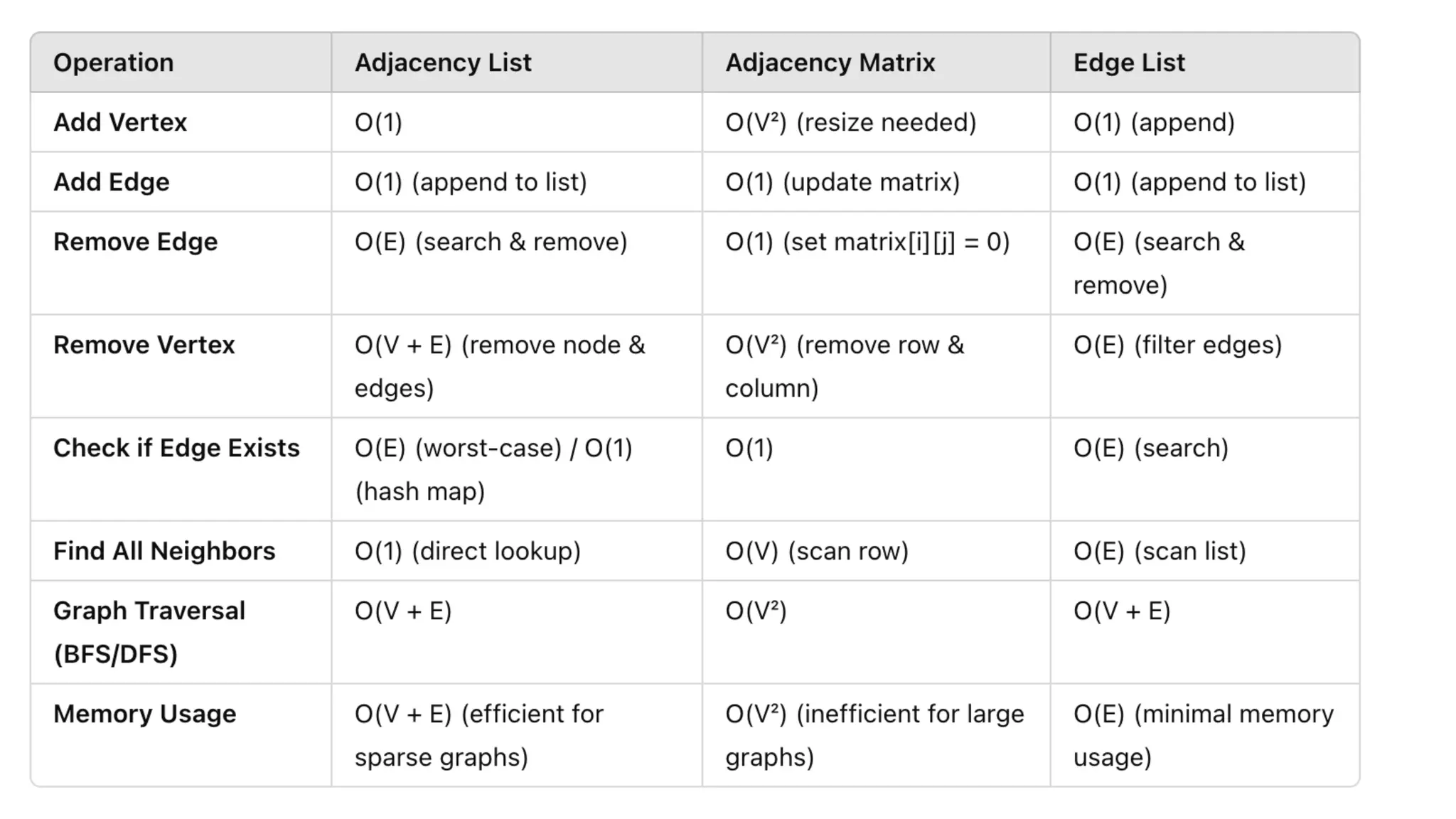
Adjacency List: This representation stores the neighbors of each node as a list.
A — B — C
|
D E
Pros: It is efficient for sparse graphs (few edges compared to nodes). Space is O(|V|+|E|), adding edges
and vertices is O(1), fast graph traversal.
Cons: No object representing edges, slower random access query than matrices.
Representation
graph = {
"A": ["B", "D"],
"B": ["A", "C", "E"],
"C": ["B"],
"D": ["A"],
"E": ["B"]
}

Adjacency Matrix: A 2D matrix where matrix[i][j] = 1 if an edge exists between nodes i and j, otherwise 0.
A — B — C
|
D E
Pros: Efficient for dense graphs (many edges). Constant time for random access, and adding/removing
edges.
Cons: Takes O(|V|^2) size, and O(|V|^2) time to add/remove vertices.
Representation

Edge List: A list of (node1, node2) pairs, optionally with weights.
A — B — C
|
D E
Pros: Memory efficient for sparse graphs (only stores existing edges).
Representation
[('A', 'B'), ('A', 'D'), ('B', 'C'), ('B', 'E')]

Breadth First Search
Breadth-First Search (BFS) is an algorithm for traversing or searching a graph
level by level (i.e., exploring all neighbors before moving deeper).
Key Characteristics:
✅ Uses a queue (FIFO) to track the next node to visit.
✅ Explores closest nodes first before moving to distant ones.

Breadth First Search
Breadth-First Search (BFS) is an algorithm for traversing or searching a graph level by
level (i.e., exploring all neighbors before moving deeper).
A
/
B C
/
D E F
If we perform BFS starting from A, the order of traversal is:
🔹 A → B → C → D → E → F
Step-by-step breakdown:
Start at
1 ️
1️⃣ A → Visit B, C (immediate neighbors)
Move to
2️⃣ B → Visit D, E
Move to
3 ️
3️⃣ C → Visit F
Move to
4️⃣ D, E, F (no new nodes left)

Pseudocode
1. Initialize a queue and add the starting node.
2. Mark the starting node as visited.
3. While the queue is not empty:
a. Dequeue a node.
b. Process the node.
c. Add all unvisited neighbors to the queue and mark them as visited.
4. Repeat until all reachable nodes are visited.

Applications
✔ Shortest Path in Unweighted Graphs (e.g., Google Maps, social networks)
✔ Web Crawling (search engines use BFS to explore webpages)
✔ Network Broadcasting (flooding packets in a computer network)
✔ AI and Game Development (finding the shortest moves in a game)
Demo

Visualization
https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visua
lize/

Depth First Search
Depth-First Search (DFS) is a graph traversal algorithm that explores as deep as
possible along each branch before backtracking.
Key Characteristics:
✅ Uses a stack (LIFO) for traversal (can be implemented using recursion).
✅ Explores one path fully before moving to another.
✅ Useful for topological sorting, cycle detection, and pathfinding.

Depth First Search
Depth-First Search (DFS) is a graph traversal algorithm that explores as deep as
possible along each branch before backtracking.
A
/
B C
/
D E F
If we perform DFS starting from A, the possible traversal order is:
🔹 A → B → D → E → C → F (one possible DFS order)
Step-by-step breakdown:
Start at
1 ️
1️⃣ A → Move deep into B
From
2 ️
2️⃣ B, visit D (deepest point)
Backtrack to
3 ️
3️⃣ B, visit E
Backtrack to
4 ️
4️⃣ A, visit C
From
5️⃣ C, visit F
All nodes visited →
6 ️
6️⃣ End

Pseudocode
1. Initialize a stack (or use recursion).
2. Push the starting node onto the stack and mark it as visited.
3. While the stack is not empty:
a. Pop a node.
b. Process the node.
c. Push all unvisited neighbors onto the stack.
4. Repeat until all reachable nodes are visited.

Applications
✔ Pathfinding (e.g., Maze solving, AI in gaming)
✔ Cycle Detection in graphs
✔ Topological Sorting (e.g., Course scheduling)
✔ Connected Components Detection
Demo

Visualization
https://www.hackerearth.com/practice/algorithms/graphs/depth-first-search/visualiz
e/

Class Activity I
Finding Shortest Paths from A to All Nodes
- Algorithm
- Time Complexity

Class Activity II
Given the course prerequisites, how to find a valid
ordering of course enrollment?
- Algorithm

Home Activity
Design an algorithm that can identify if a graph has a cycle or not.
Possible Application
Imagine you're building a project management system for a large company, where multiple teams are
working on different tasks. These tasks have dependencies — some tasks need to be completed before
others can start. You need to determine whether the task dependency graph has a cycle, meaning a set
of tasks that depend on each other in a circular way, making it impossible to complete the tasks.
In this scenario, detecting cycles in the task dependency graph is crucial because if there's a cycle,
some tasks will never be completed, leading to project delays and potential failures. Identifying and
resolving such cycles can ensure that the project progresses smoothly.

Given (connected) graph G(V,E),
a spanning tree T(V’,E’):
› Is a subgraph of G; that is, V’ V, E’ E.
⊆ ⊆
› Spans the graph (V’ = V)
› Forms a tree (no cycle);
› So, E’ has |V| -1 edges

Minimum Spanning Tree
• Edges are weighted: find minimum cost
spanning tree
• Find the subset of edges that connects all
vertices with the least cost.
• Applications
› Find cheapest way to wire your house
› Find minimum cost to send a message on the Internet

Prim’s Algorithm
• Build tree incrementally
› Pick lower cost edge connected to known (incomplete)
spanning tree that does not create a cycle and expand
to include it in the tree
• Step 1: Choose an arbitrary vertex as the starting point.
• Step 2: Mark it as visited and add the smallest edge connecting to an
unvisited vertex.
• Step 3: Repeat for each unvisited vertex, adding the smallest edge that
connects to the MST.
• Step 4: Continue until all vertices are in the MST.

Prim’s algorithm
Starting from empty T,
choose a vertex at
random and initialize
V = {1), E’ ={}

Prim’s algorithm
Choose the vertex u not in
V such that edge weight
from u to a vertex in V is
minimal (greedy!)
V={1,3} E’= {(1,3) }

Prim’s algorithm
Repeat until all vertices have
been chosen
Choose the vertex u not in V
such that edge weight from v to a
vertex in V is minimal (greedy!)
V= {1,3,4} E’= {(1,3),(3,4)}
V={1,3,4,5} E’={(1,3),(3,4),(4,5)}
….
V={1,3,4,5,2,6}
E’={(1,3),(3,4),(4,5),(5,2),(2,6)}

Prim’s algorithm
Repeat until all vertices have
been chosen
V={1,3,4,5,2,6}
E’={(1,3),(3,4),(4,5),(5,2),(2,6)}
Final Cost: 1 + 3 + 4 + 1 + 1 = 10

Prim’s algorithm Analysis
• If the “Select the unmarked node u with minimum cost” is done
with binary heap then O((n+m)logn)

Basic Graph Algorithms Vertex (Node): lk

More Related Content

Similar to Basic Graph Algorithms Vertex (Node): lk

Recently uploaded

Basic Graph Algorithms Vertex (Node): lk