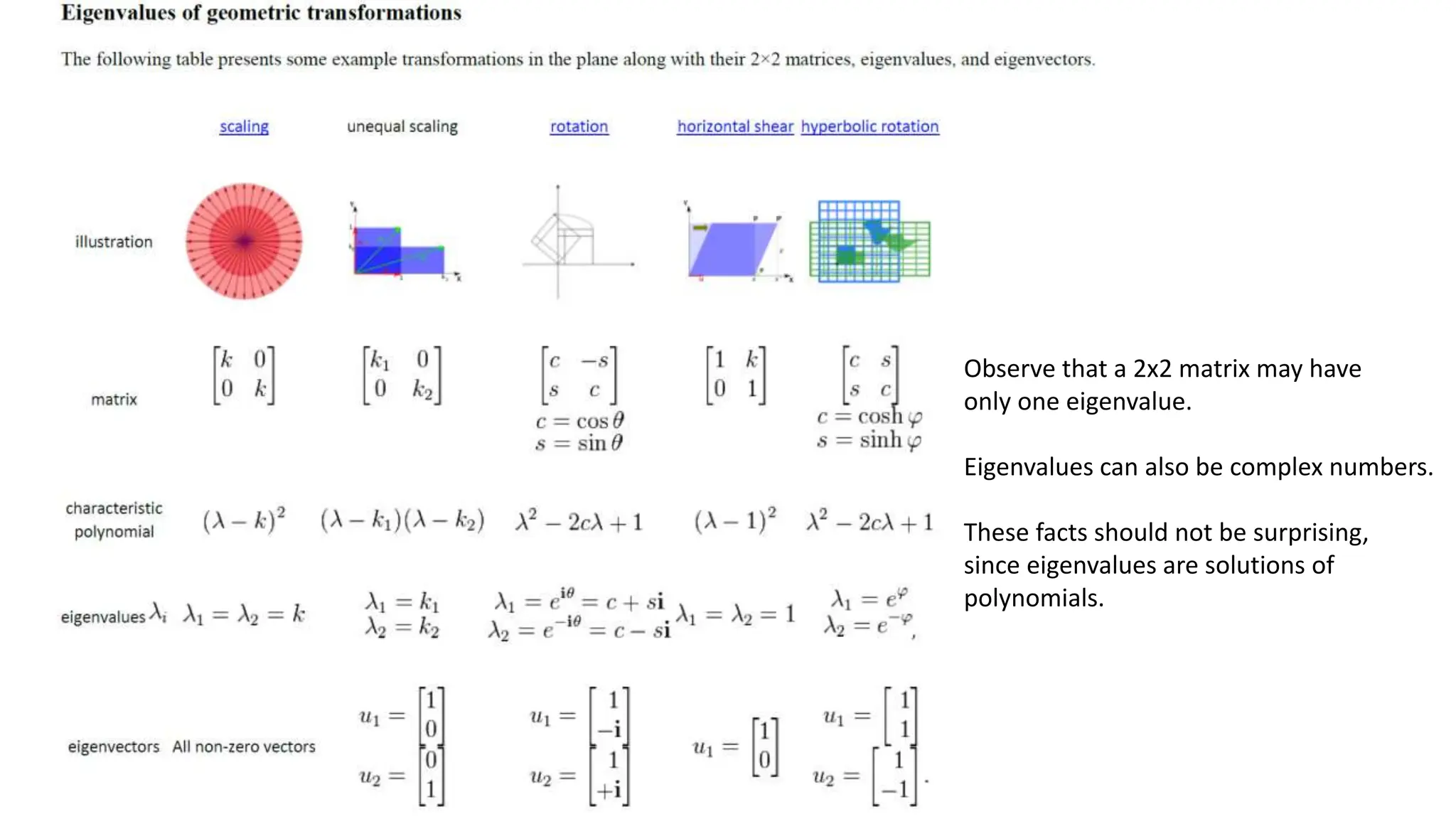
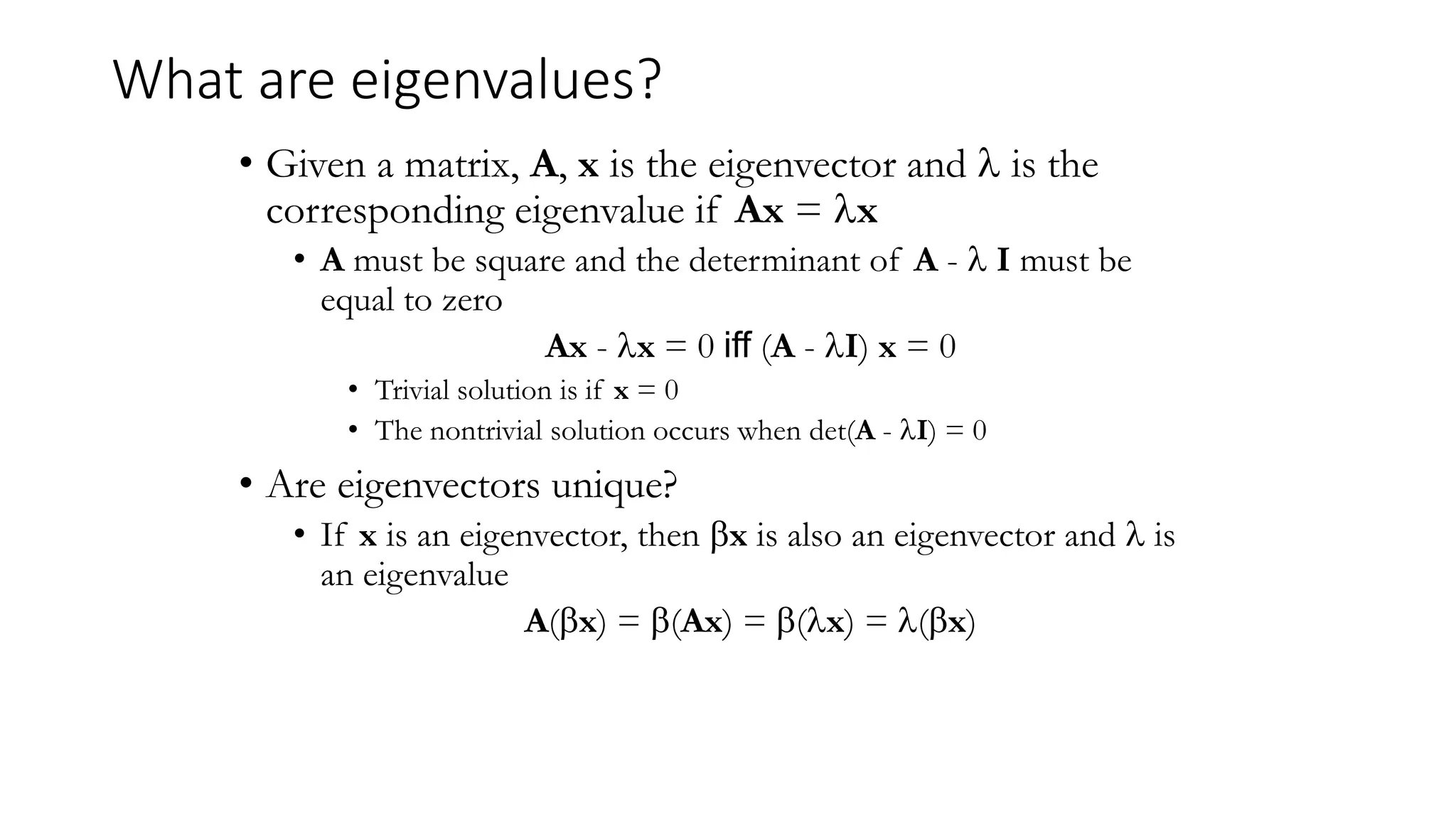Chapter 4 discusses the fundamentals of matrix algebra, focusing on eigenvalues and eigenvectors. It explains the conditions for the existence of nontrivial solutions to the eigenvalue equation and introduces the characteristic equation for calculating eigenvalues. Additionally, it highlights numerical methods for determining eigenvalues for larger matrices, detailing the limitations of explicit algebraic formulas and the development of efficient computational algorithms.