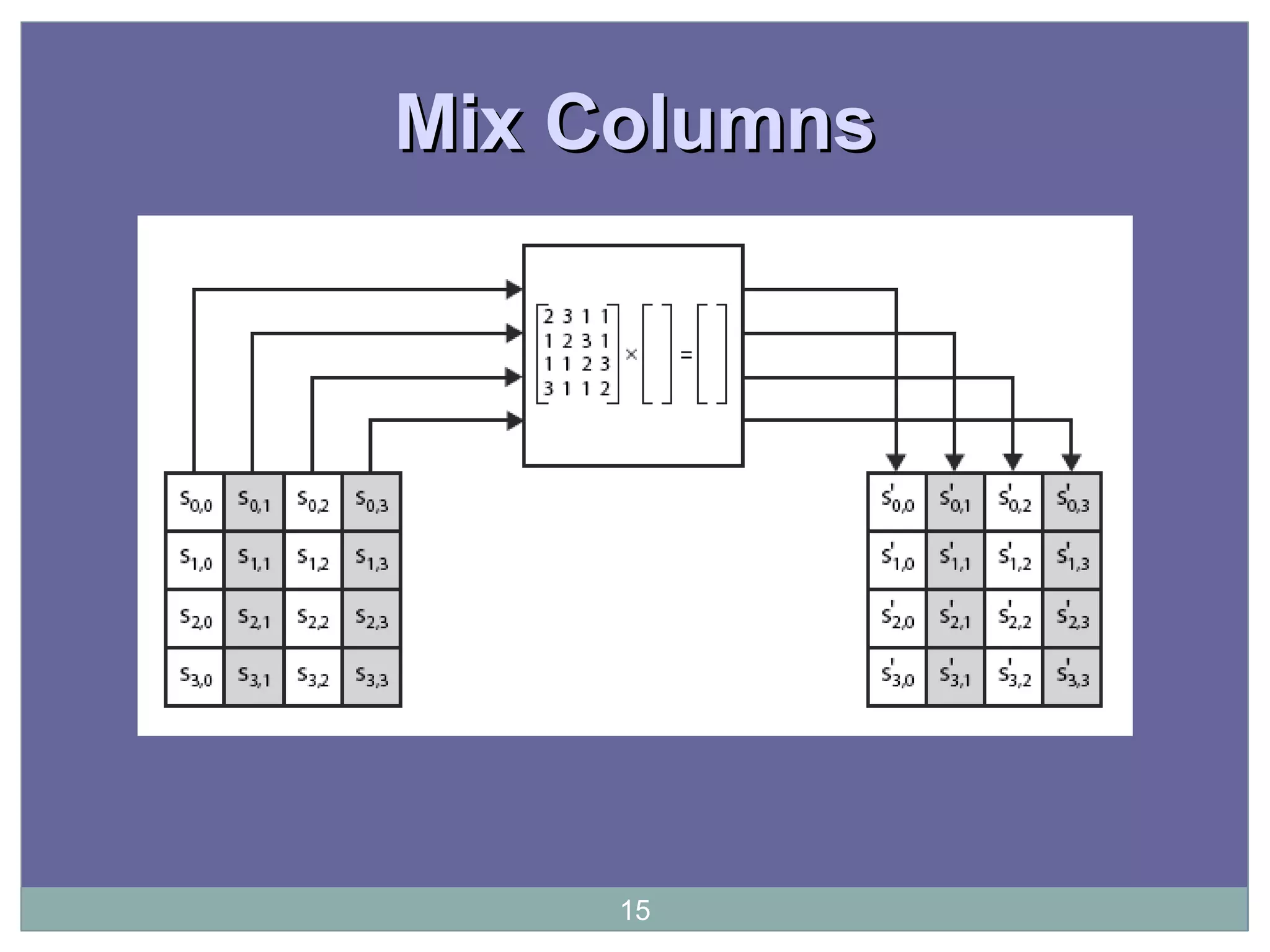
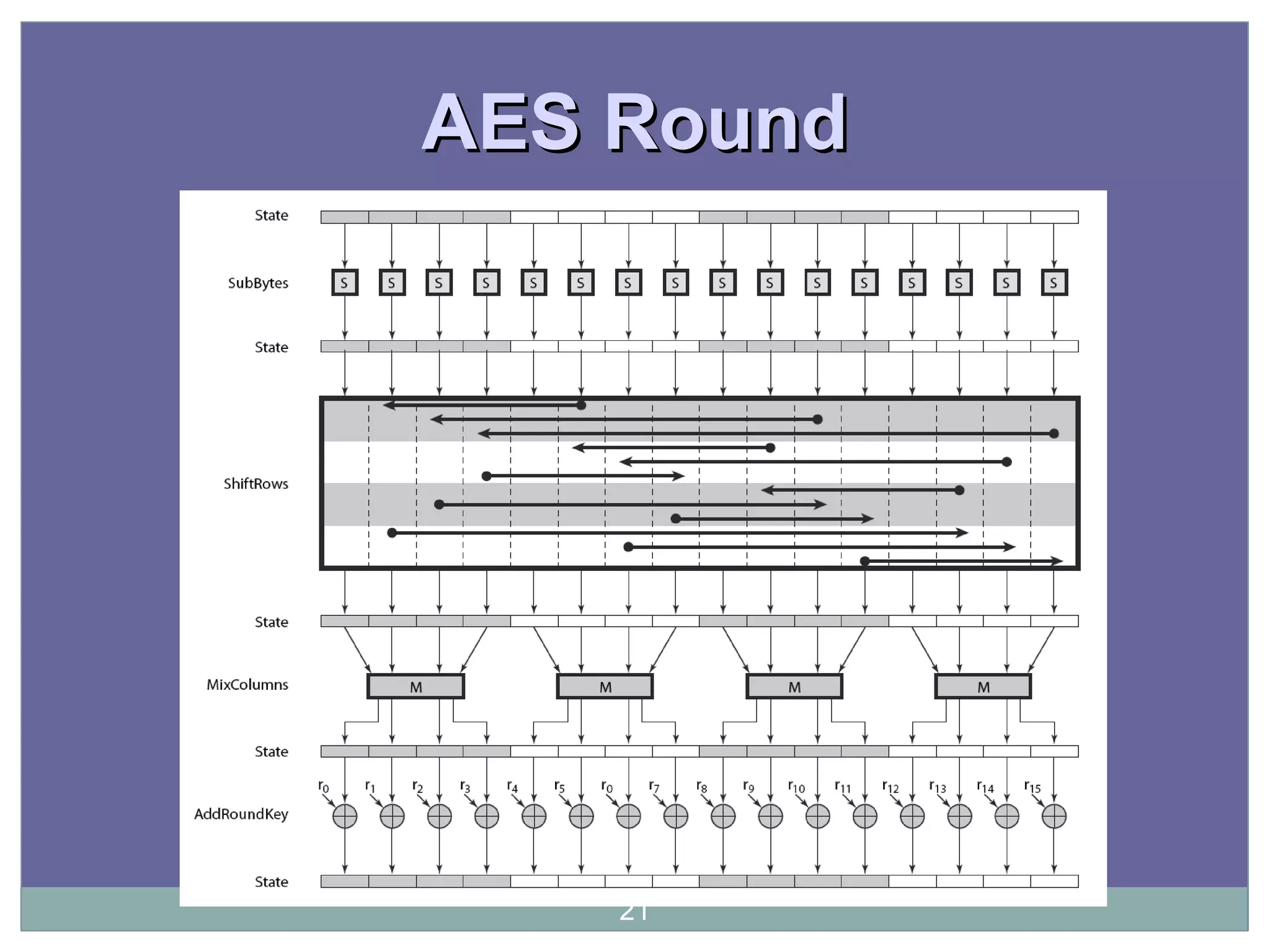
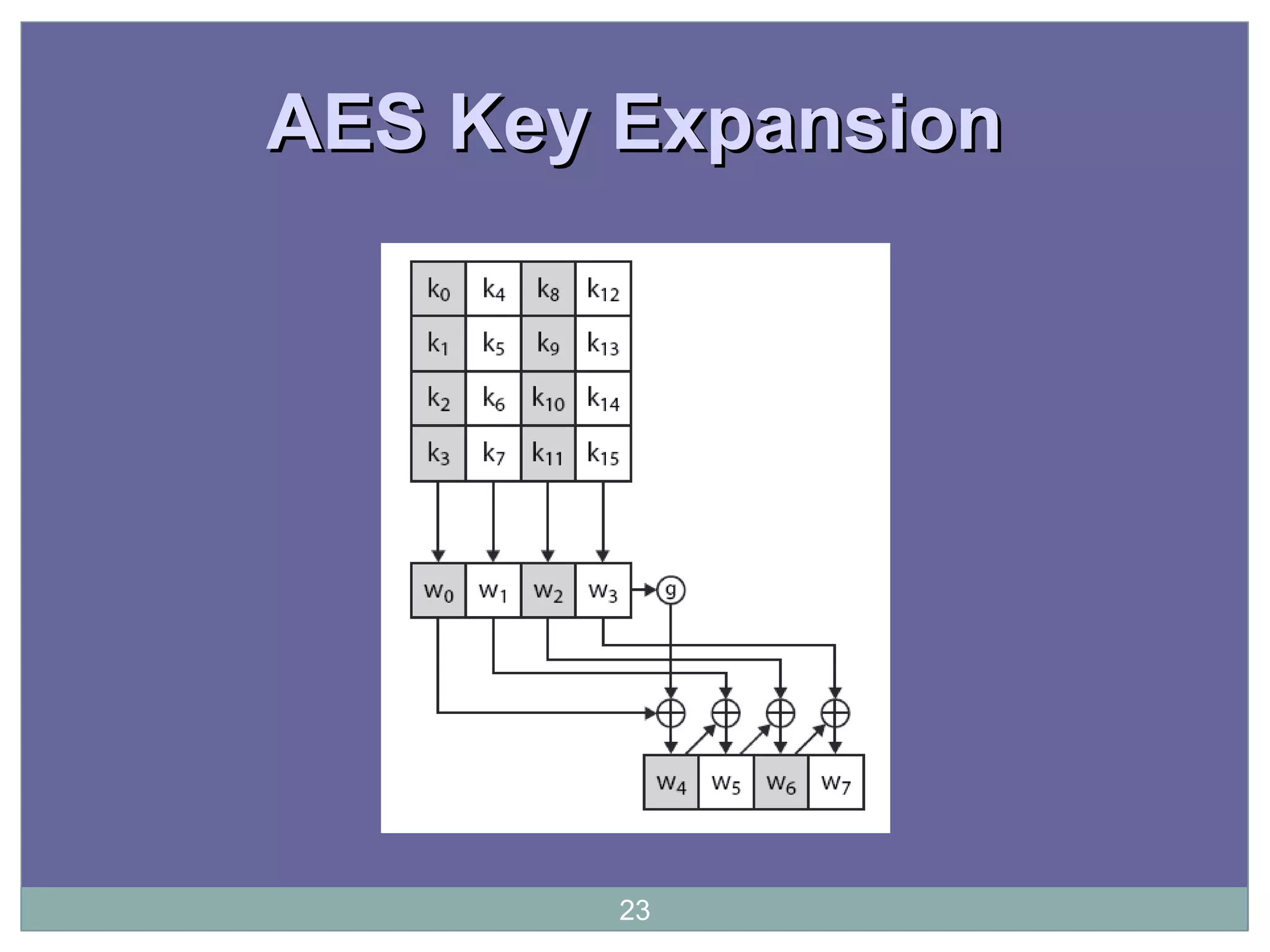
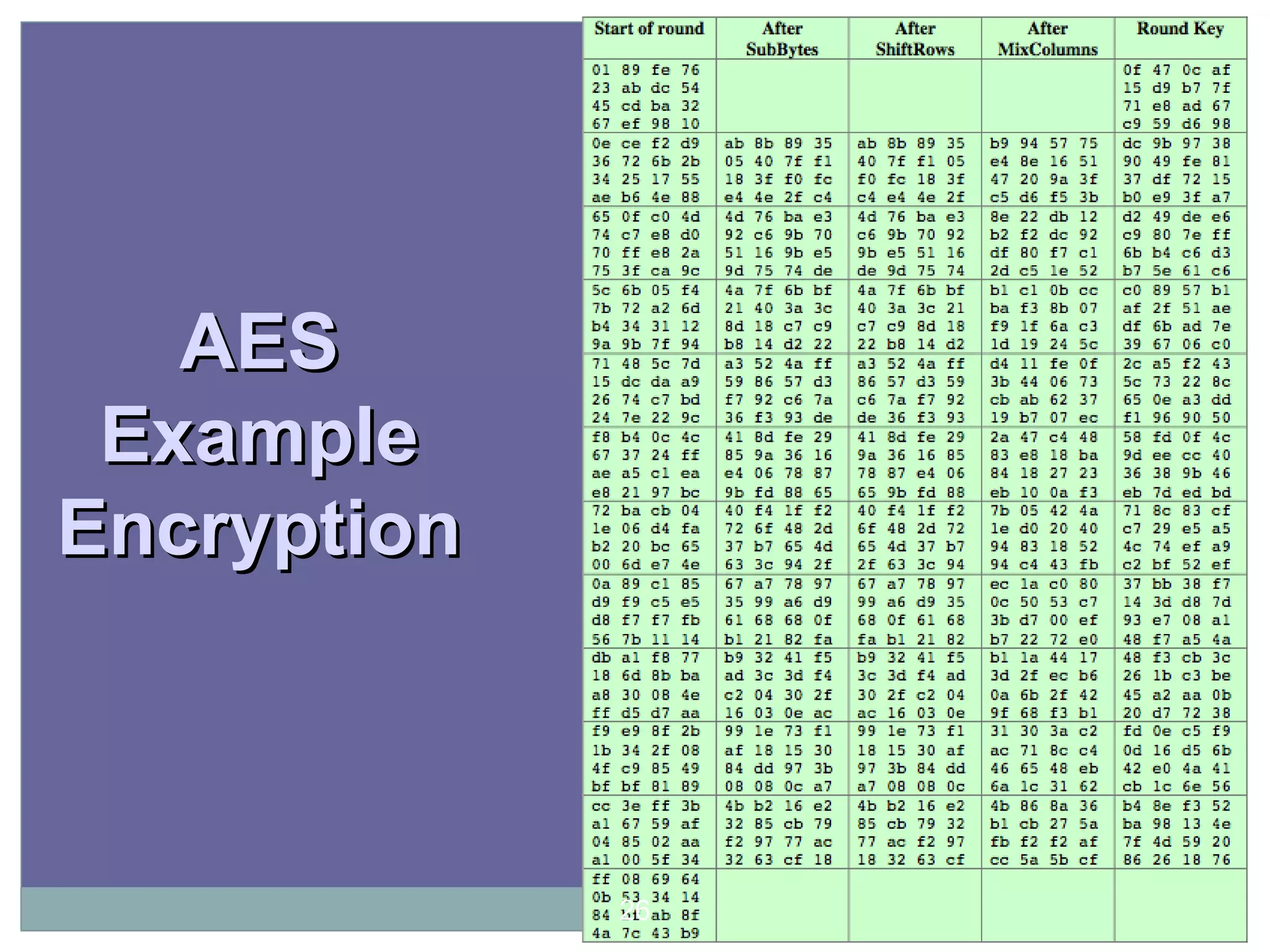
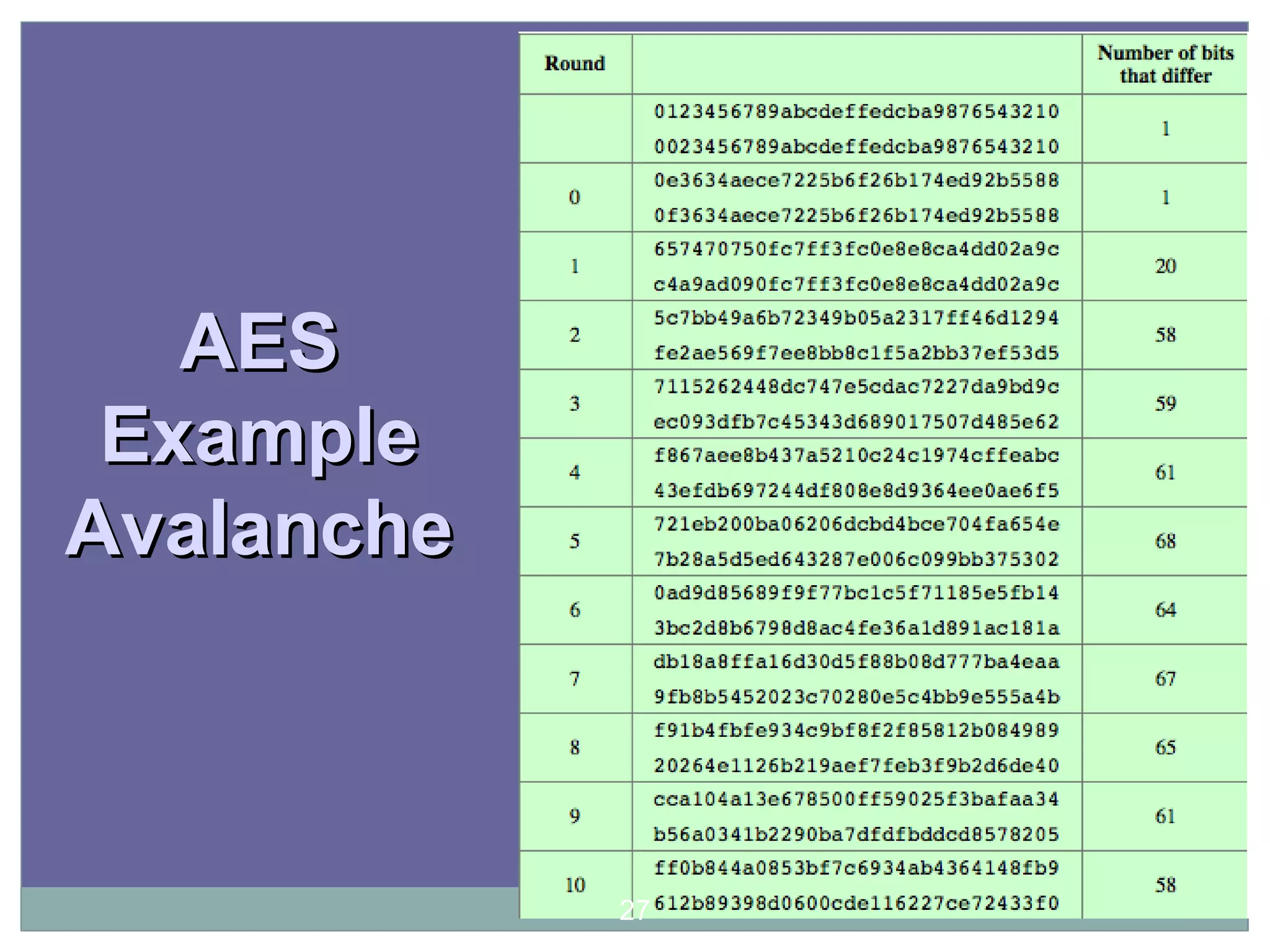
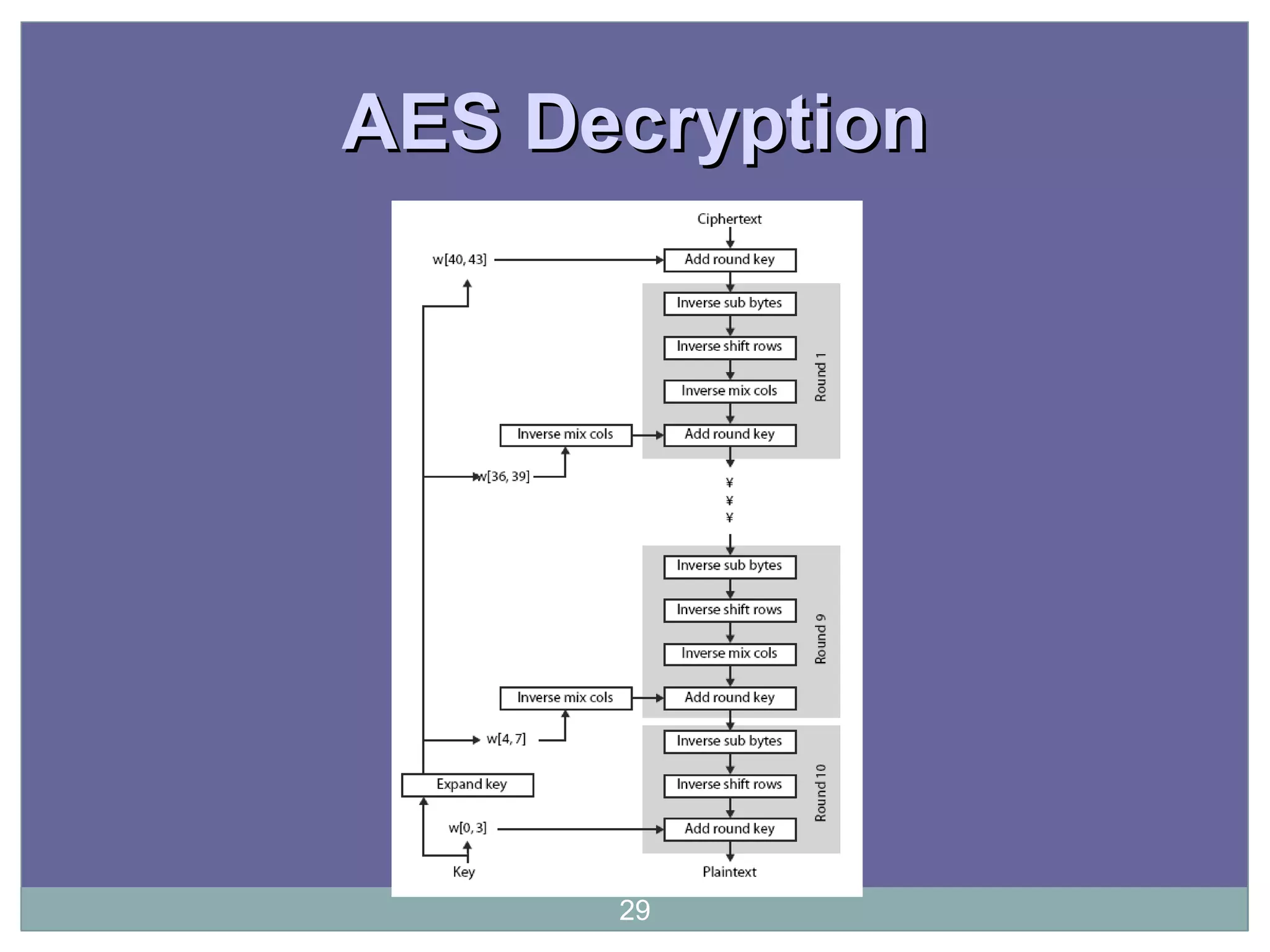
The document discusses the Advanced Encryption Standard (AES), which was selected by the US National Institute of Standards and Technology (NIST) in 2000 to replace the Data Encryption Standard (DES). AES uses 128-bit blocks and supports key sizes of 128, 192, and 256 bits. It is based on the Rijndael cipher designed by Vincent Rijmen and Joan Daemen. AES operates on a 4x4 column-major order matrix of bytes and uses substitutions, transpositions, and mixing operations along with adding a round key to transform the input, with decryption being the inverse process using the round keys in reverse order.