The document summarizes research on encrypting controllers using RSA public-key cryptography. It presents:
1) The problem of encrypting control signals and parameters to conceal a system's dynamics from attackers.
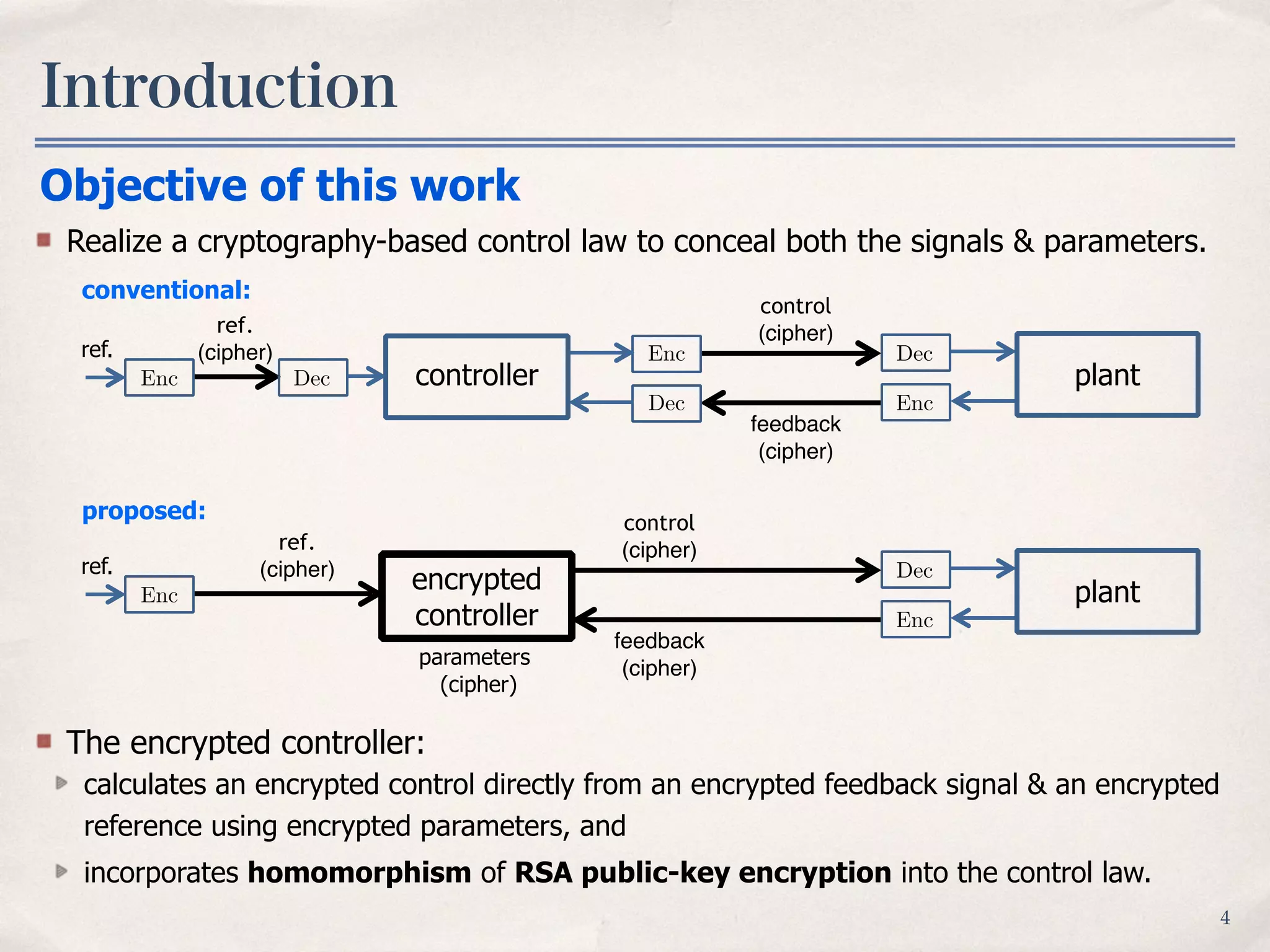
2) A proposed encrypted controller that calculates encrypted control signals directly from encrypted feedback and reference using encrypted parameters and the homomorphic properties of RSA encryption.
3) Simulations showing the encrypted controller functions properly while hiding internal signals and parameters, and validation that system identification is not possible without the private key.


![Introduction
3
Controller device is important, but exposed to threats of hacking and targeted attacks.
signals: interruption, modeling, stealing recipe, management policy and know-how
parameters: knowledges about system designs and operations
Attacks to networked control system
plantcontroller
ref. (recipe)
control signals
feedback signals
parameters
[1] Sandberg et al., 2015. [2] Sato et al., 2015. [3] Pang et al., 2011
Related works
aiming to conceal the signals
control-theoretical approach: detection[1], positive use of noises[2]
cryptography-based approach: encryption of communication links[3]
no studies trying to encrypt the controller itself…
control
(cipher)
feedback
(cipher)
EncDec
Enc Dec
plantcontroller
ref.
ref.
(cipher)
Enc Dec](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-3-2048.jpg)
![Problem Statement
5
Encryption of controller
Consider a feedback control law :
K: scalar gain k : discrete time
: scalar plant output
: scalar control inputu
y
f
Controller encryption problem:
Given an encryption scheme , for a control law realize an encrypted law .fE fE
Define an encrypted control law , given an encryption scheme , satisfyingfE
fE (Enc(K), Enc(y)) = Enc(f(K, y))
5
control
(cipher)
feedback
(cipher)
Enc
Dec
plant
parameters
(cipher)
fE (Enc(K), Enc(y))
Enc(y)
Enc(u) u
y
Enc(K)
E
.
u[k] = f(K, y[k]) := Ky[k]](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-5-2048.jpg)
![RSA-Encrypted Controller
6[4] Rivest, “A Method for Obtaining Digital Signatures and Public-Key Cryptosystem”, 1978. [5] Rivest, “On Data Banks and Privacy Homomorphisms”, 1978.
RSA public-key encryption
RSA encryption scheme[4,5] (Rivest-Shamir-Adelman cryptosystem)
key generation: public keys , , and private key (prime numbers)
encryption:
decryption:
e n d
m
c
: integer in plaintext space
: integer in ciphertext space
Homomorphism of the RSA encryption[5]
Enc(m1 ⇥ m2) = Enc(m1) ⇥ Enc(m2) mod n
Assumed that and , then the following holds.m1 = K m2 = y
fE (Enc(K), Enc(y)) := Enc(K) ⇥ Enc(y) mod n
= Enc(K ⇥ y) = Enc(u)
c = Enc(m) = me
mod n
m = Enc(c) = cd
mod n](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-6-2048.jpg)
![RSA-Encrypted Controller
7
a 2 N
b•e : round function
KpM = ba ⇥ Kpe
yM[k] = ba ⇥ y[k]e
uM[k] = KpMyM[k]
Kp
y[k]
u[k] = Kpy[k]
example: , then .Kp = 0.83, a = 1000 KpM = b1000 ⇥ 0.83e = 830
Remarks
Signals & parameters are real; Plaintext is integer.
need a map: multiplying by a natural number and rounding off to an integer, i.e.,
with and sufficient large, rounding (quantization) error can be made small.
Enc(uM[k]) = Enc(KpM)Enc(yM) mod n
a
encrypted
controller
u[k]
y[k]
Enc
Dec
Enc(KpM)
Enc(yM[k])
Enc(uM[k])
a 2
yM[k]
uM[k]
ba•e
plant
n](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-7-2048.jpg)
![Simulation: Controller Encryption
8
Enc(KpM) = (ba ⇥ Kpe)e
mod n = 36364958n = 94399927 e = 587 d = 42929459
(key length 27bit)
Things seen in controller
Kp = 0.83
Enc(KpM) = 36364958
encrypted
controller
Enc(KpM)
Enc(yM[k])
Enc(uM[k])
0 10 20 30
0
5
10
x 10
7
Enc(uM[k])
time[s]
−1
0
1
0 10 20 30
0
5
10
x 10
7
Enc(yM[k])
time[s]
−1
0
1
u[k]y[k]
normal:
proposed:
Kp
u[k]
y[k]
controller
a = 1000](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-8-2048.jpg)
![Validation: Protection from Stealing
9
Result of system identification (n4sid)
−150
−100
−50
0
50
10
−1
10
0
10
1
10
2
10
3
−270
−180
−90
0
original closed loop system
without encryption
with encryption
frequency[rad/s]
gain[dB]phase[deg]](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-9-2048.jpg)
![Conclusion
10
0 10 20 30
0
5
10
x 10
7
Enc(uM[k])
time[s]
−1
0
1
0 10 20 30
0
5
10
x 10
7
Enc(yM[k])
time[s]
−1
0
1
u[k]y[k]
−150
−100
−50
0
50
10
−1
10
0
10
1
10
2
10
3
−270
−180
−90
0
original closed loop system
without encryption
with encryption
frequency[rad/s]
gain[dB]phase[deg]
Introduction
Problem Statement
controller encryption problem
RSA-Encrypted Controller
homomorphism of RSA encryption
remarks in quantization error
Simulation & Validation
enable to conceal signals & parameters inside
the controller device in terms of cryptography.
enable to hide dynamics of the control system.
Future works
conceal control operations perfectly.
extend to linear and polynomial control laws.](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-10-2048.jpg)
![Simulation: Computation Cost
11
0 500 1000 1500 2000 2500 3000
0
1
2
3
4
x 10
−4
steps(sampling interval : 10ms)
computationaltime[s]
MATLAB R2014a Intel Core i5 3.2GHz RAM16GB](https://image.slidesharecdn.com/150604asccslide-150603061719-lva1-app6892/75/Controller-encryption-using-RSA-public-key-encryption-scheme-Asian-Control-Conference-2015-11-2048.jpg)