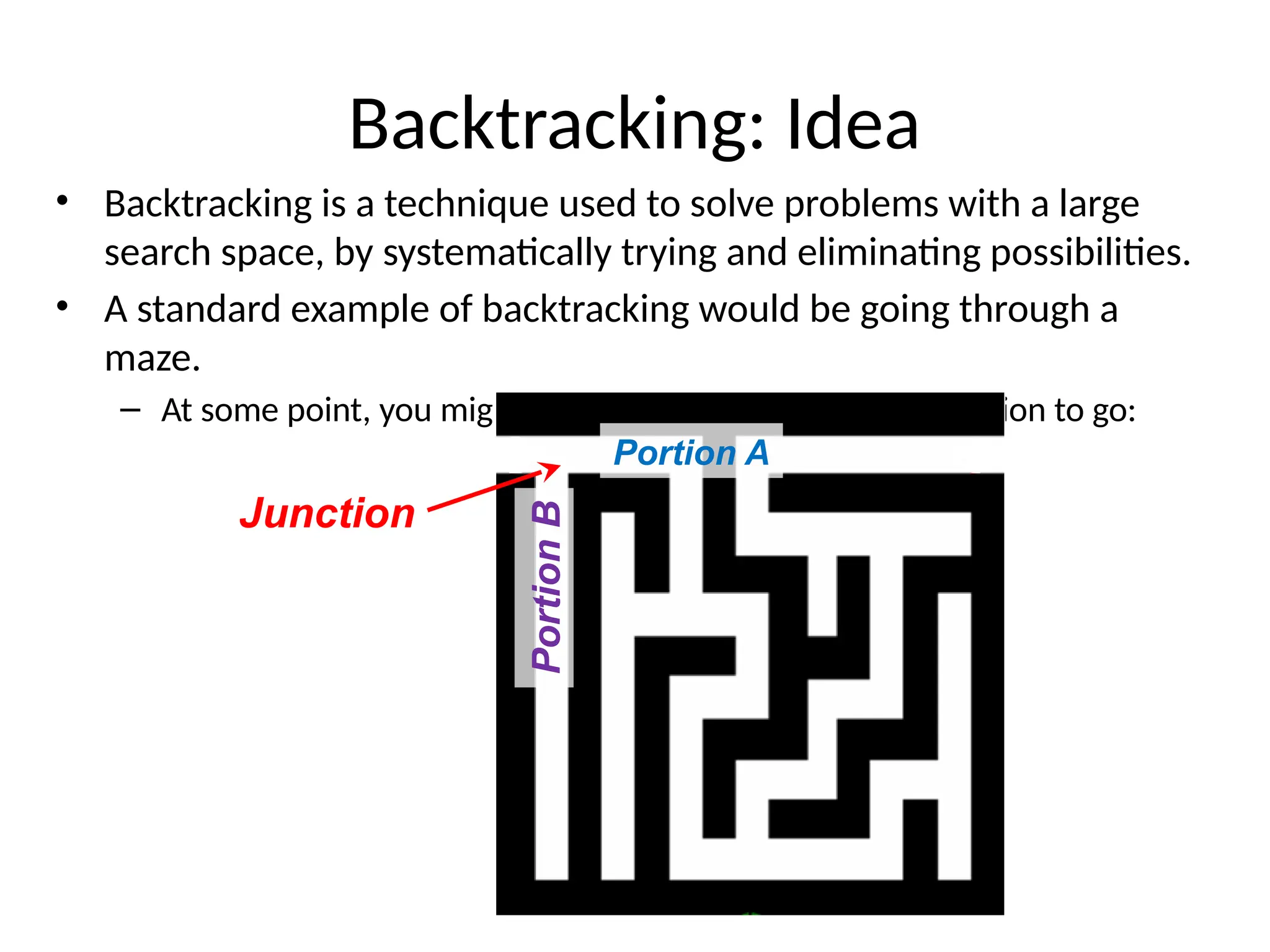
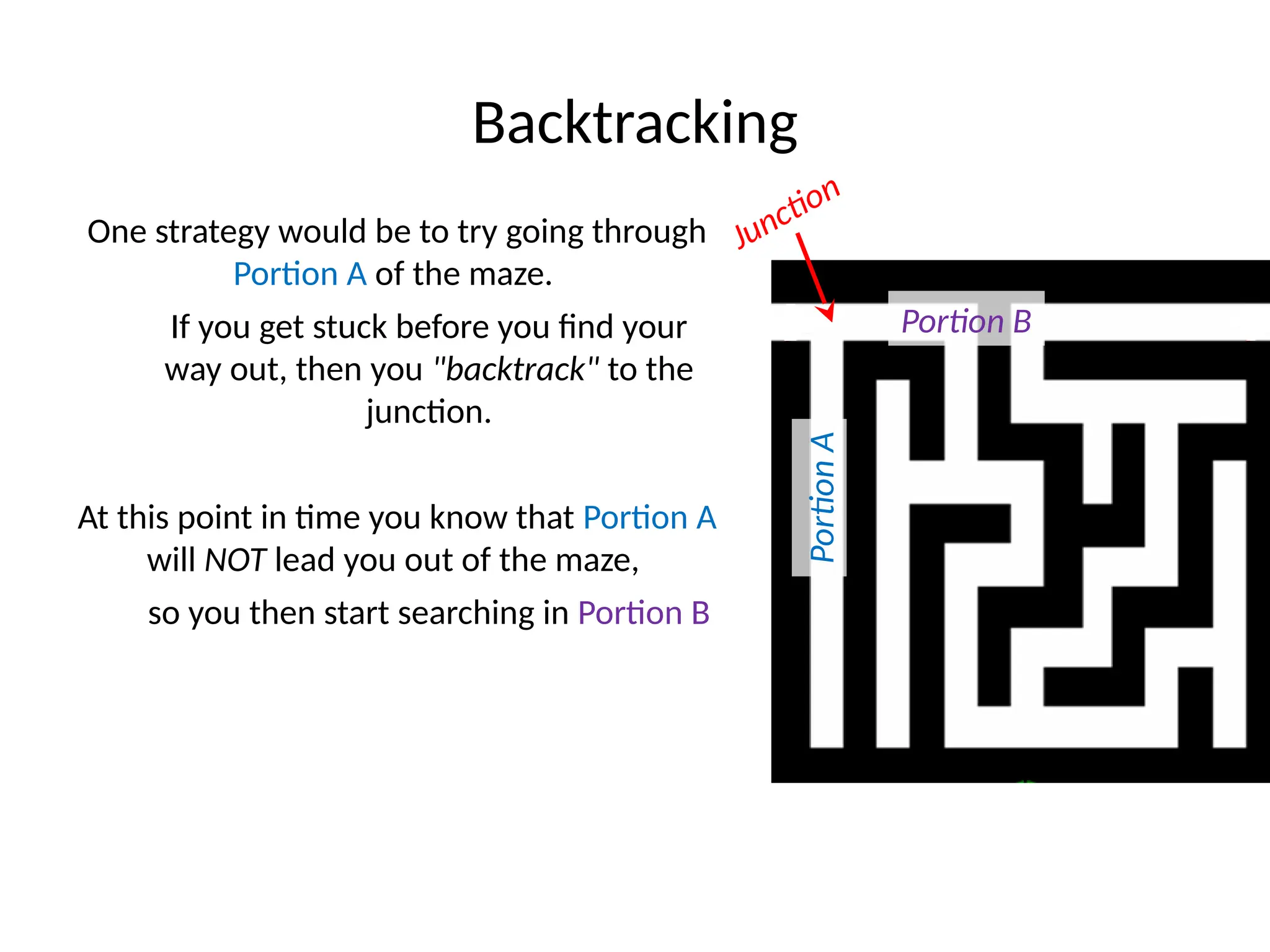
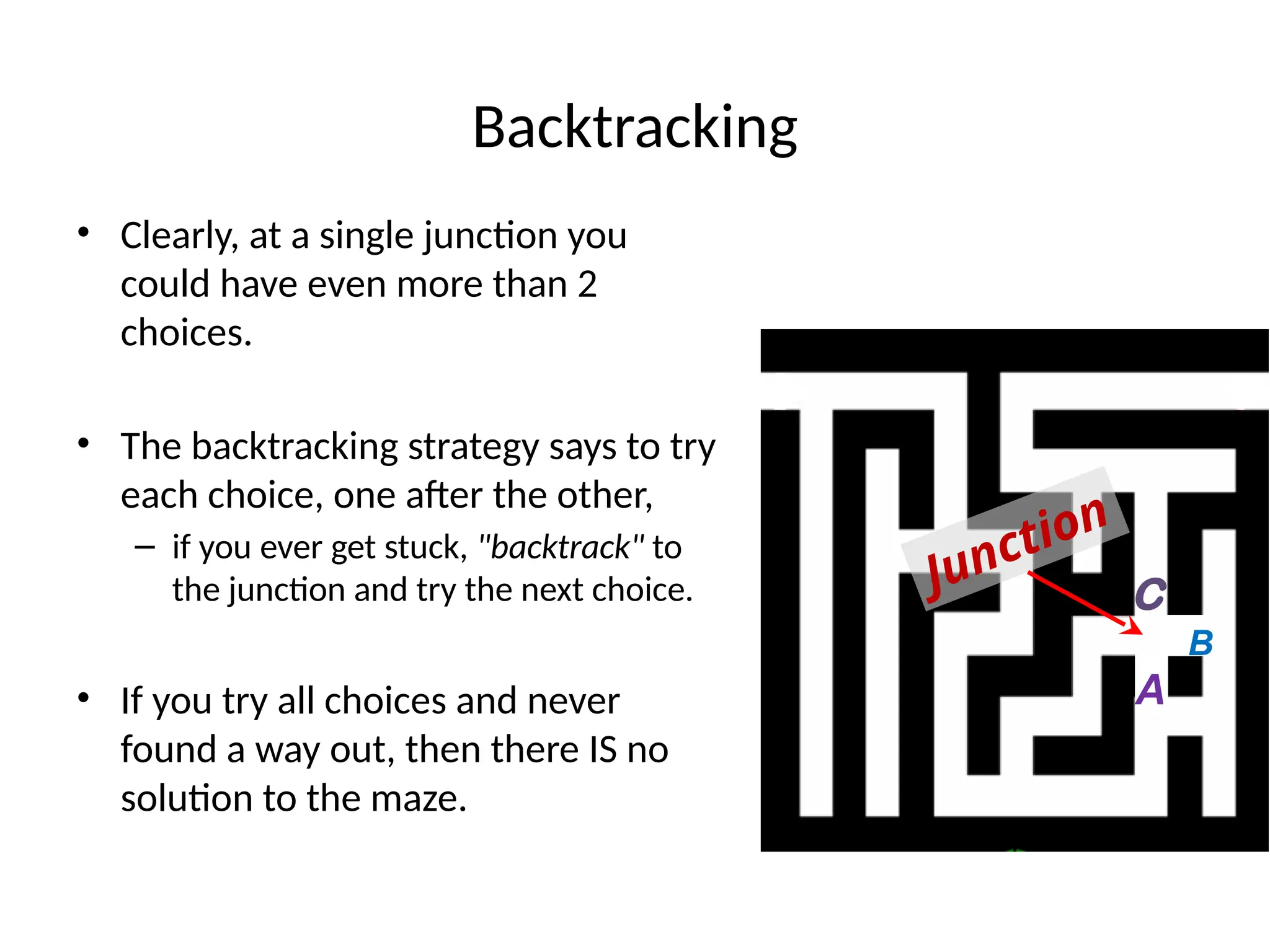
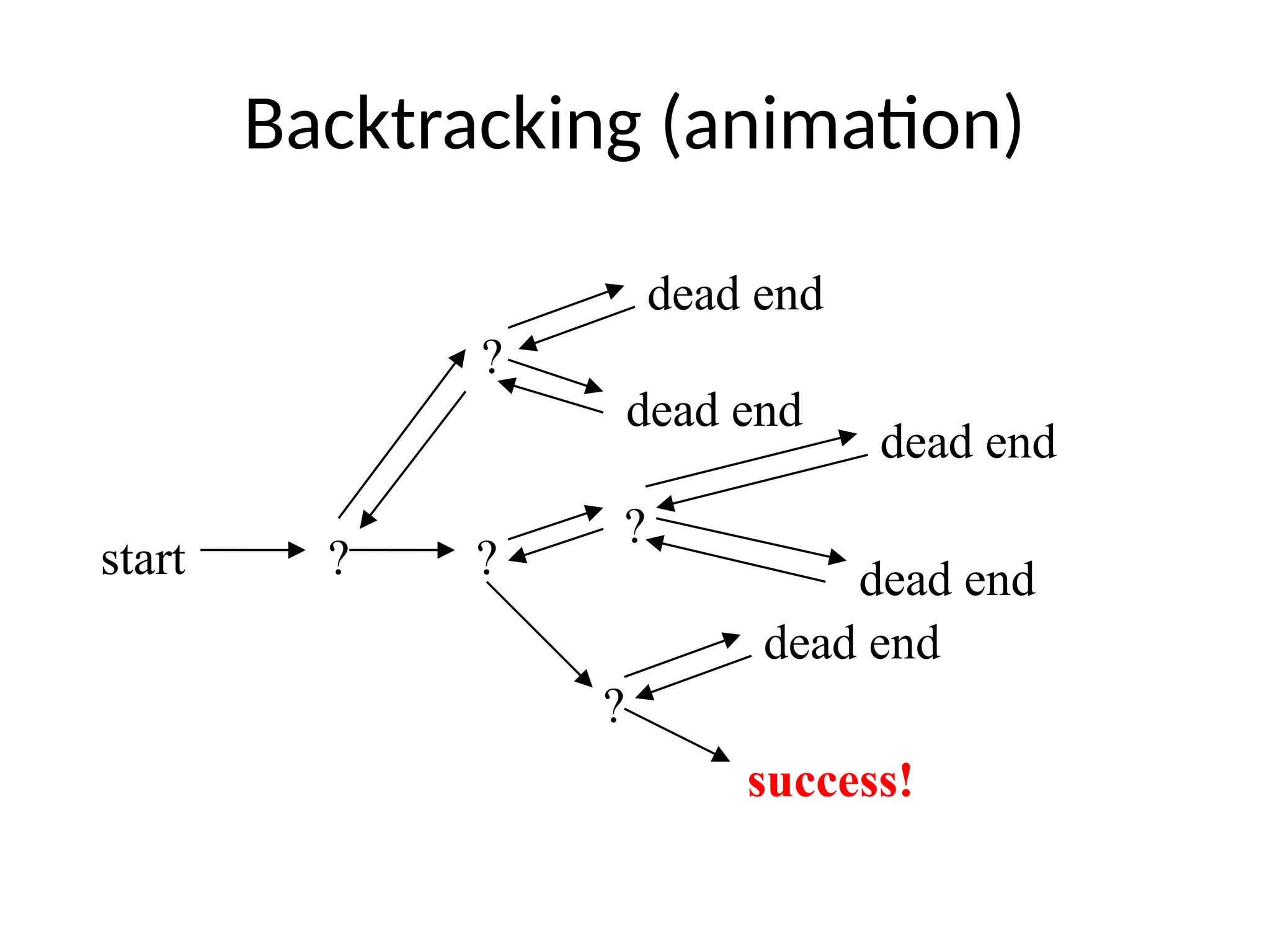
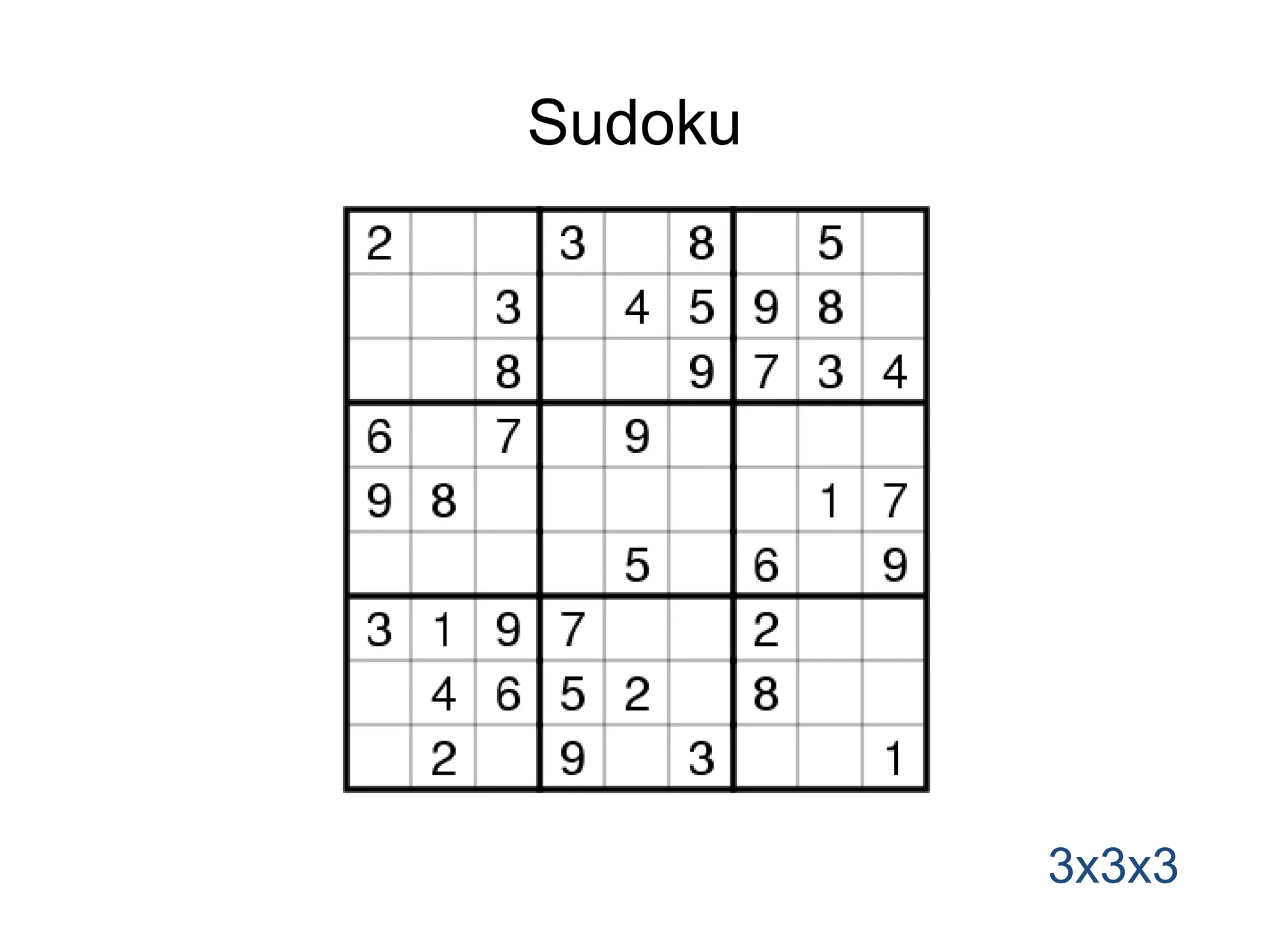
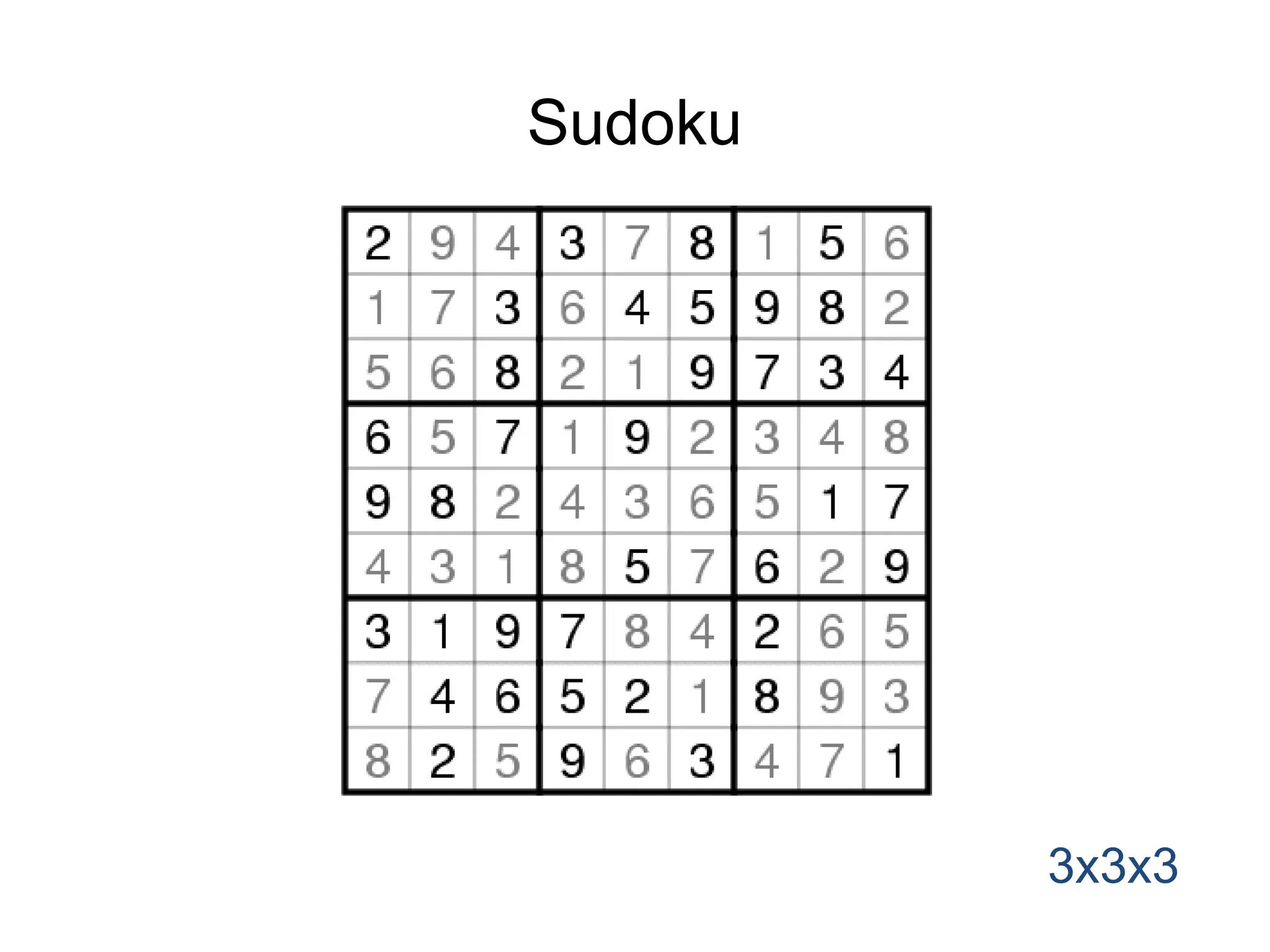
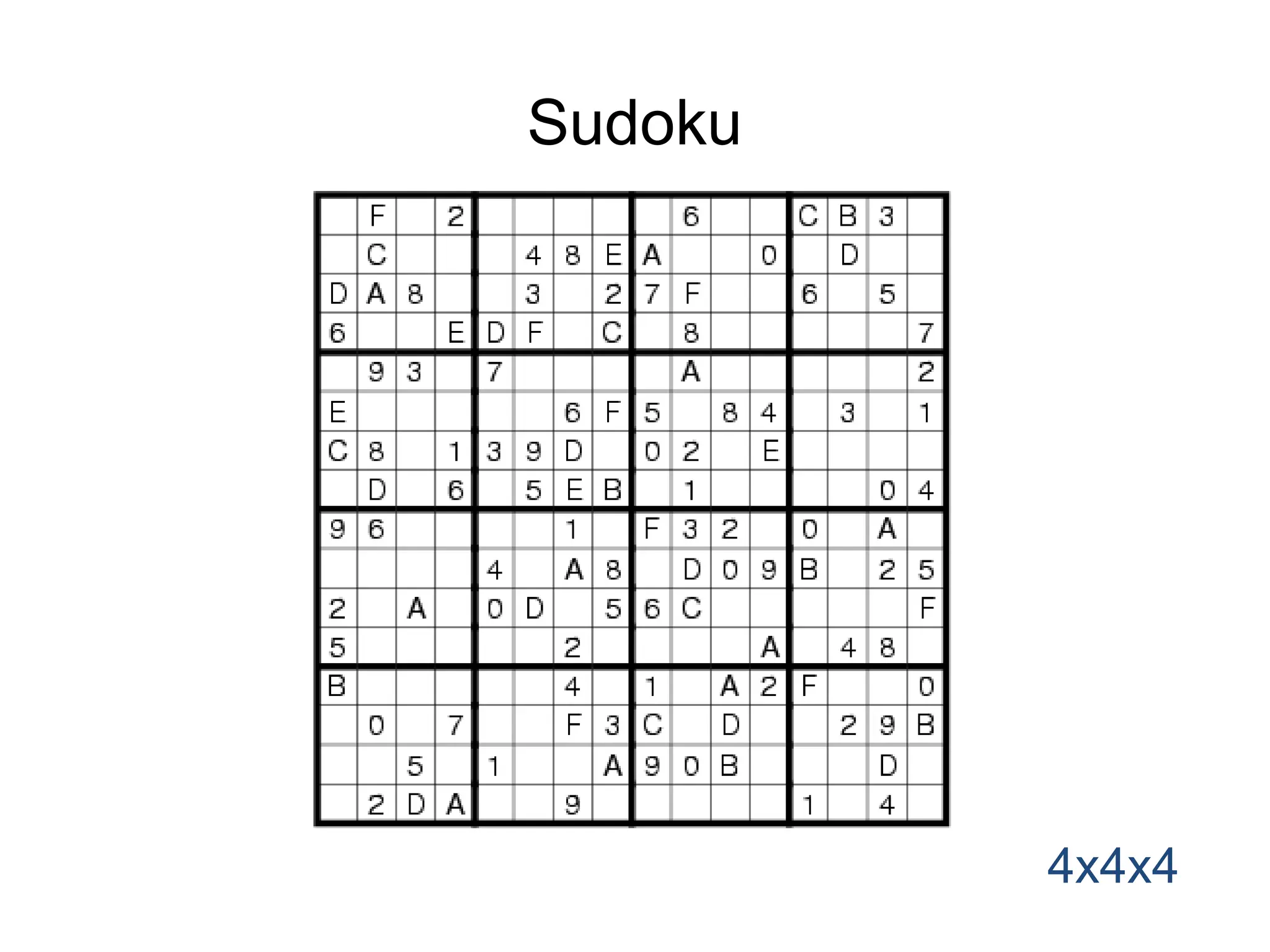
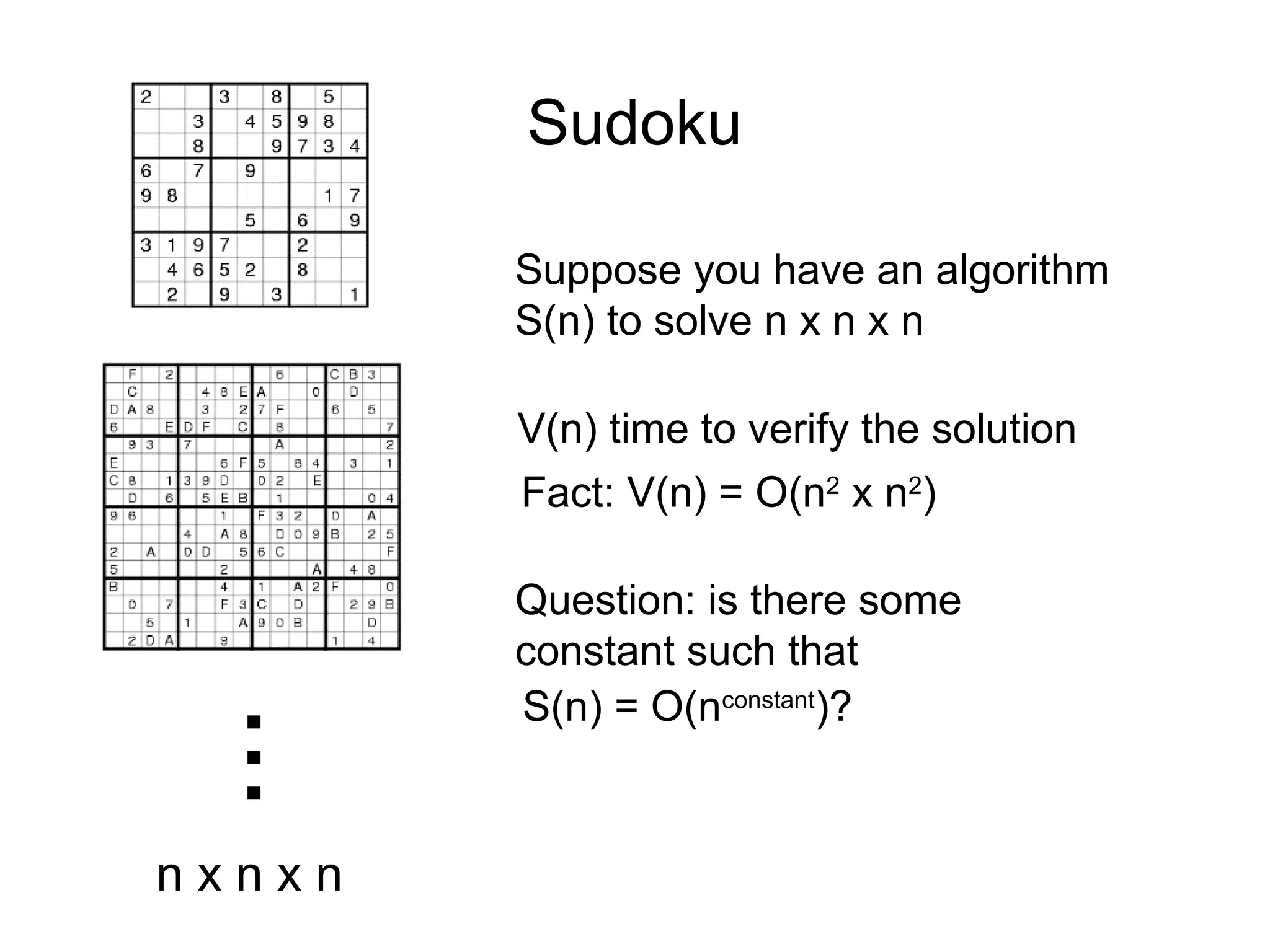
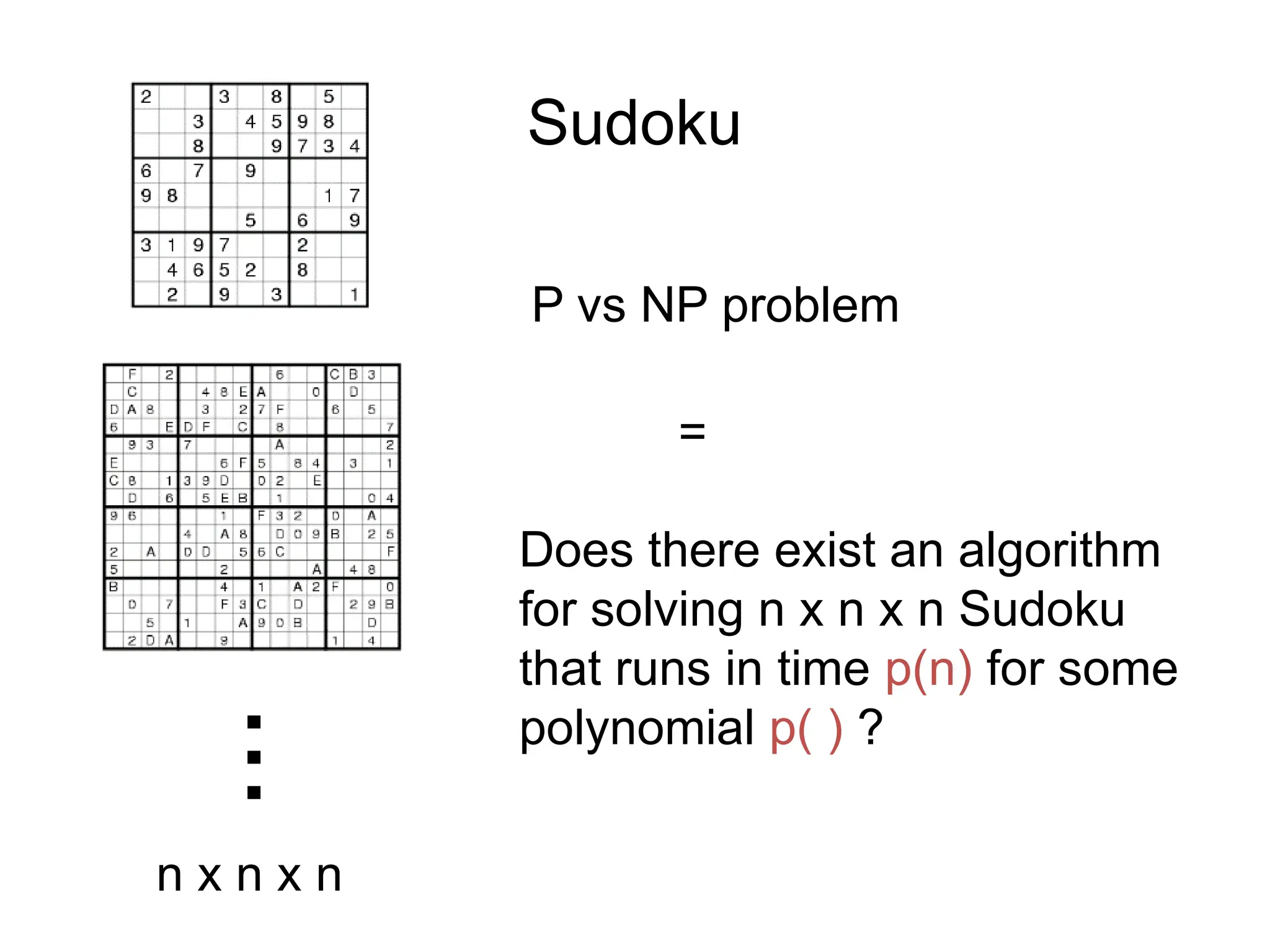
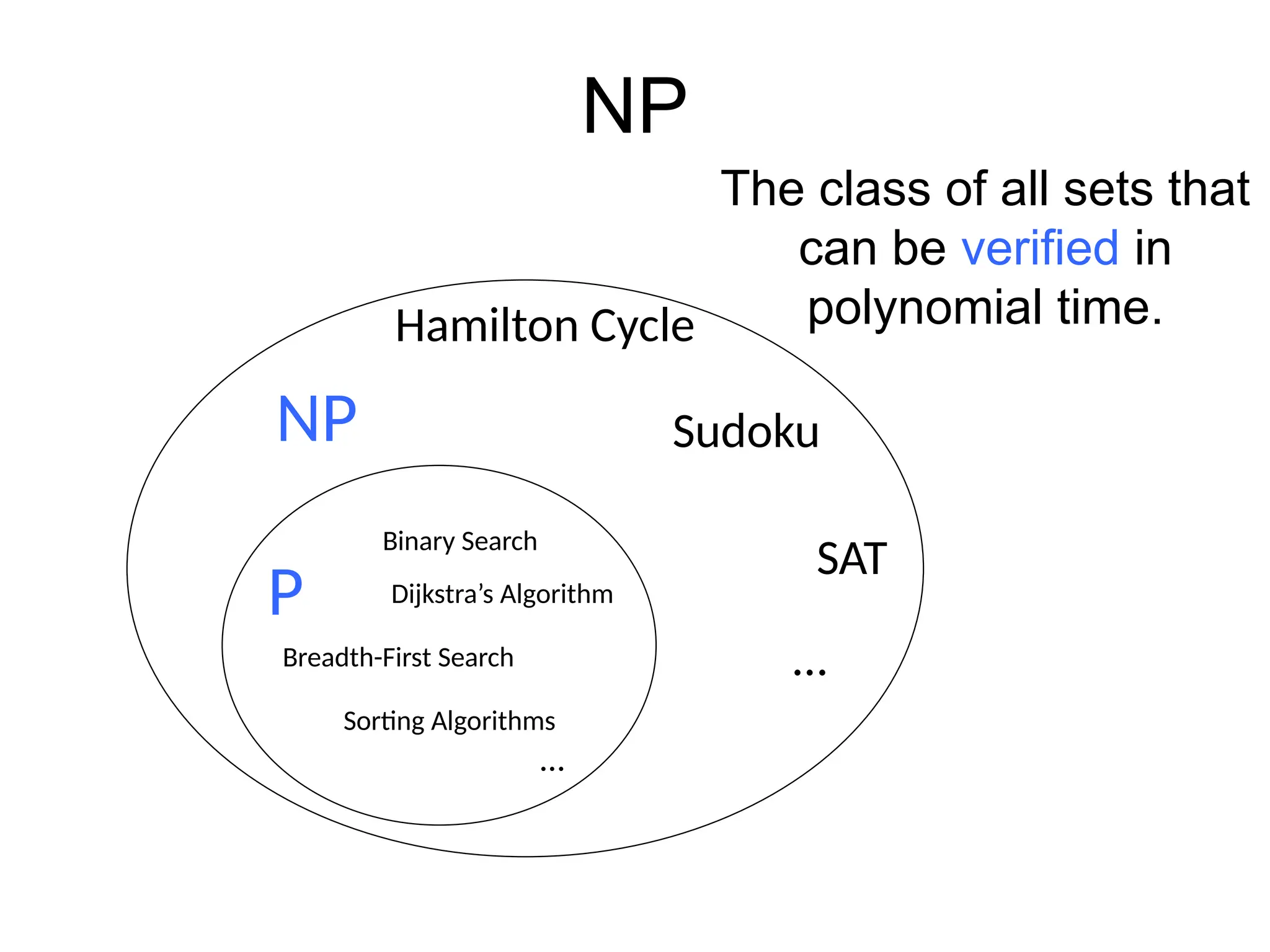
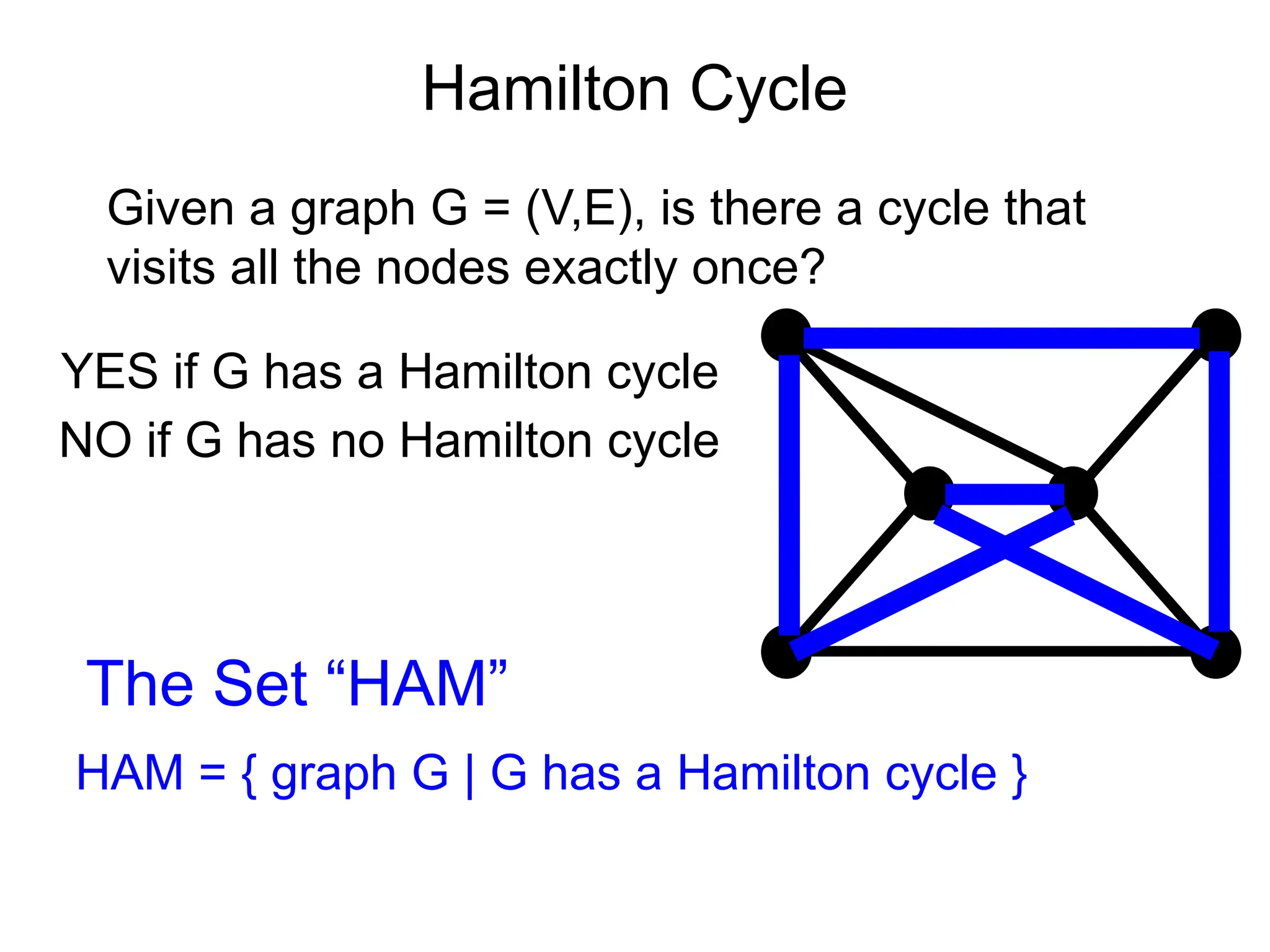
The document discusses various algorithm design techniques, focusing on backtracking as a method to solve problems with large search spaces. It also explores the P vs NP question, detailing the relationship between polynomial time solvable problems and NP-completeness, mentioning examples such as Sudoku and Hamilton cycles. The document emphasizes the significance of understanding these concepts, as solving NP-complete problems has vast implications in computer science and mathematics.










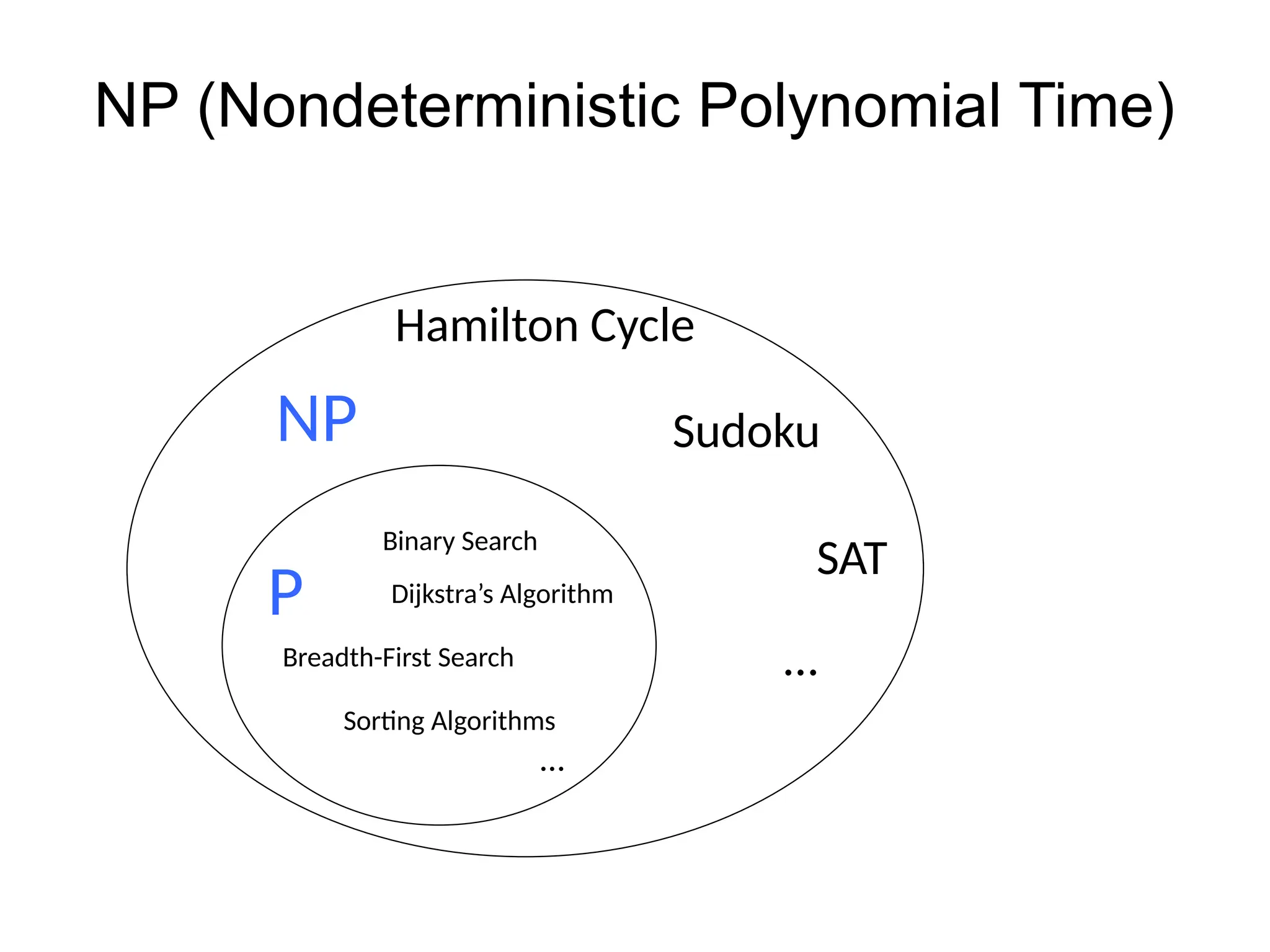













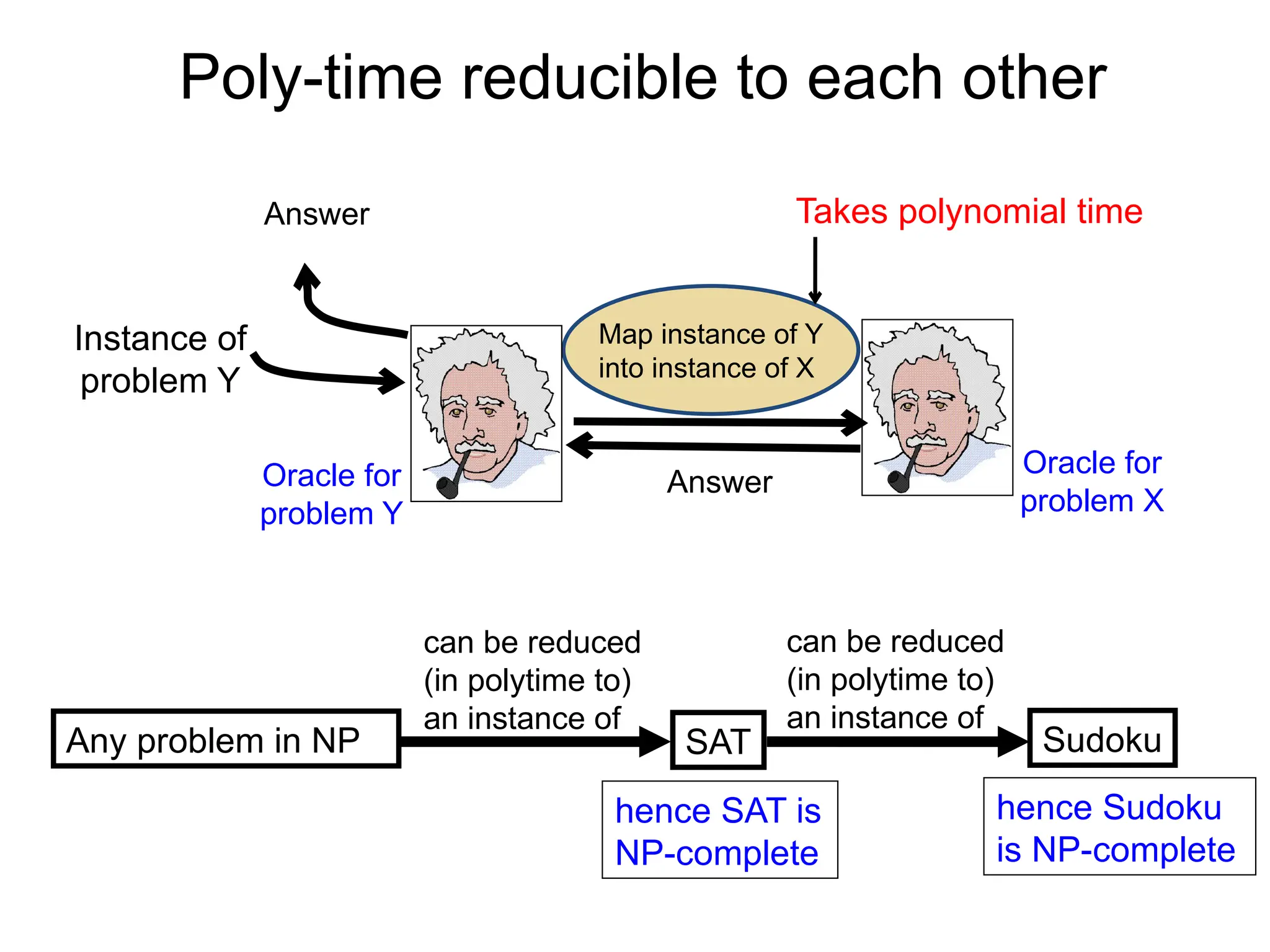
![Theorem [Cook/Levin]
SAT is one problem in NP, such that if we can show SAT
is in P, then we have shown NP = P.
SAT is a problem in NP that can capture all other
languages in NP.
We say SAT is NP-complete.](https://image.slidesharecdn.com/lecture22-240919170614-0b51af57/75/Data-structure-and-algorithms-lecture22-presentation-37-2048.jpg)