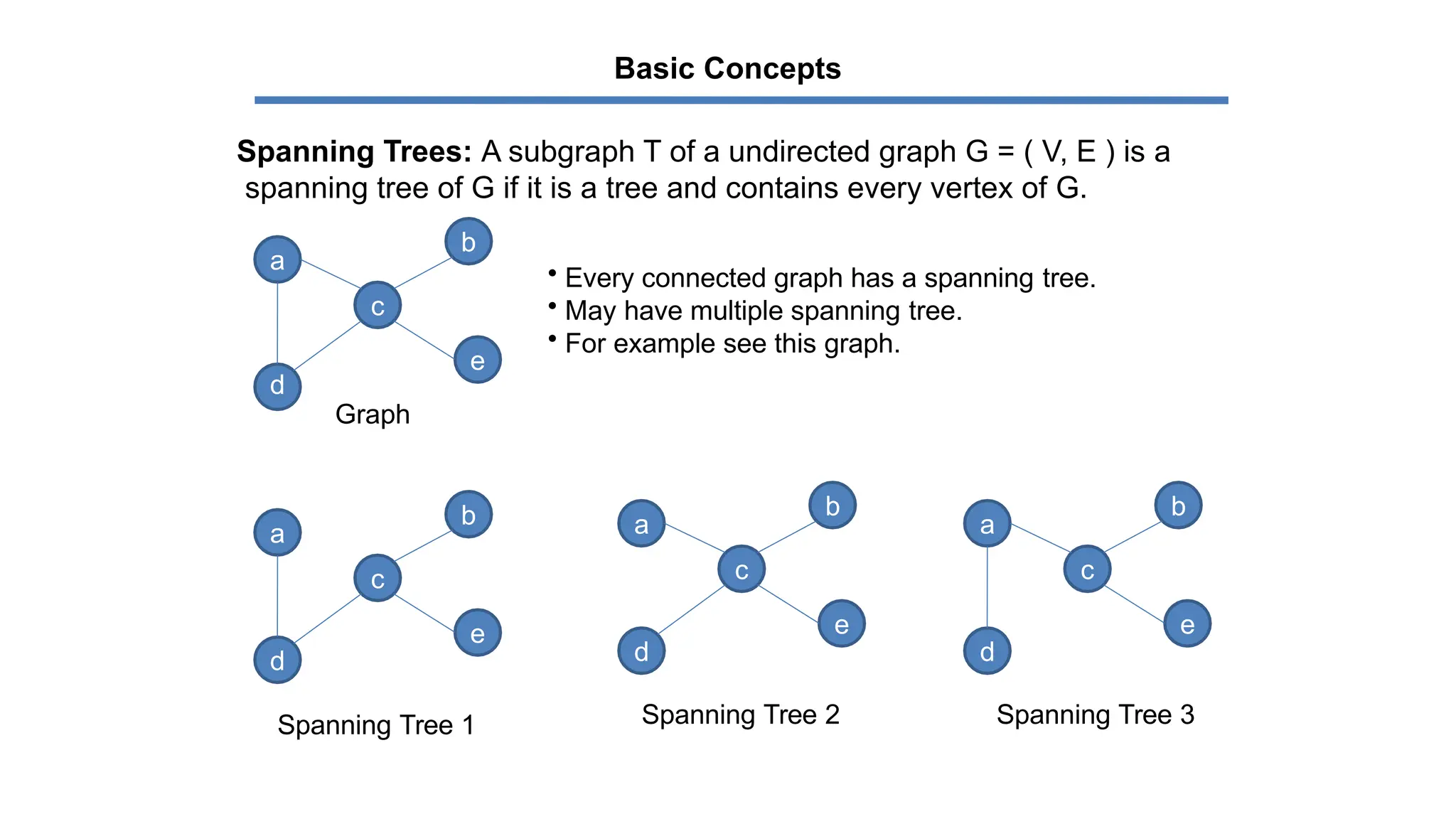
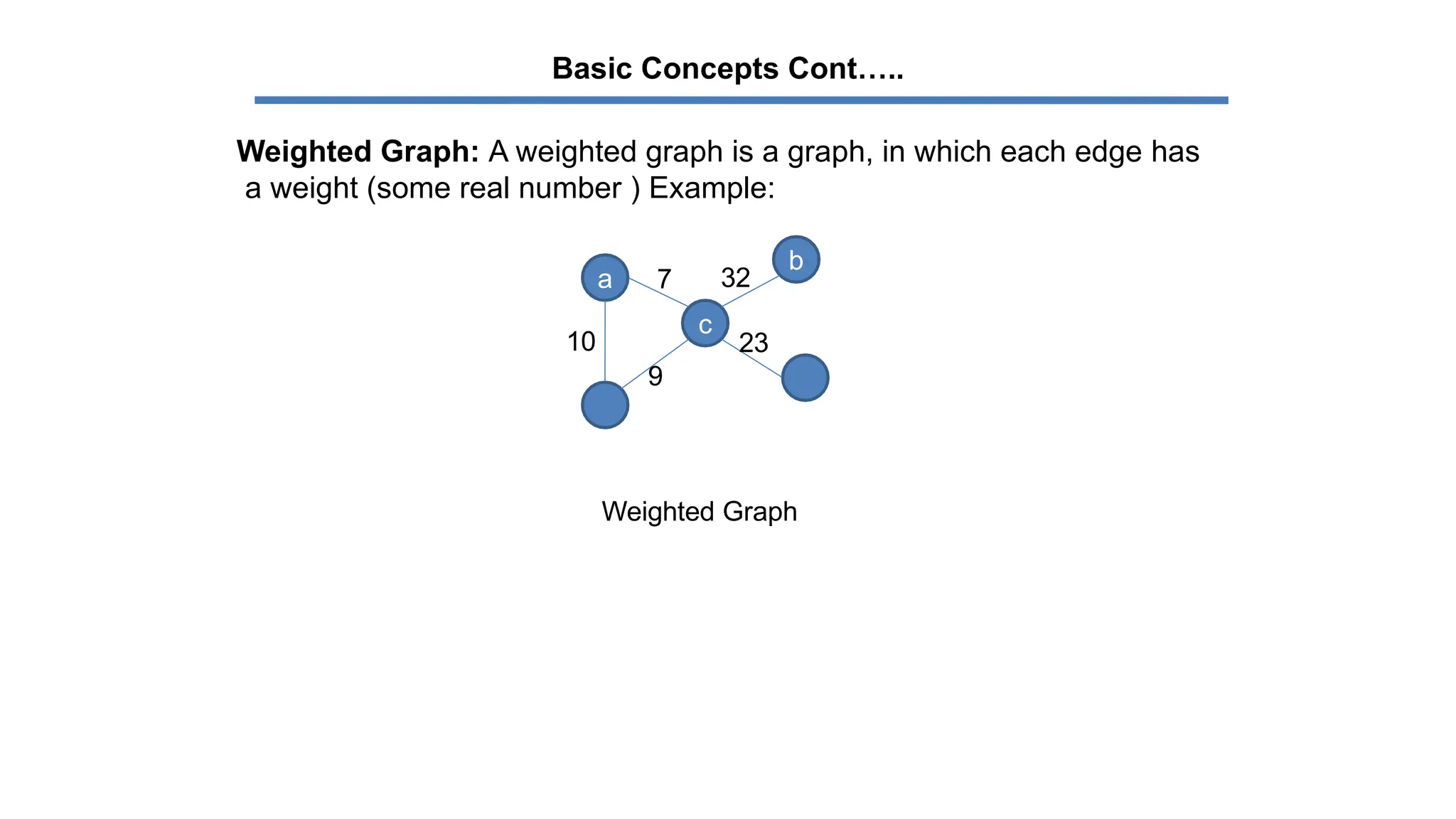
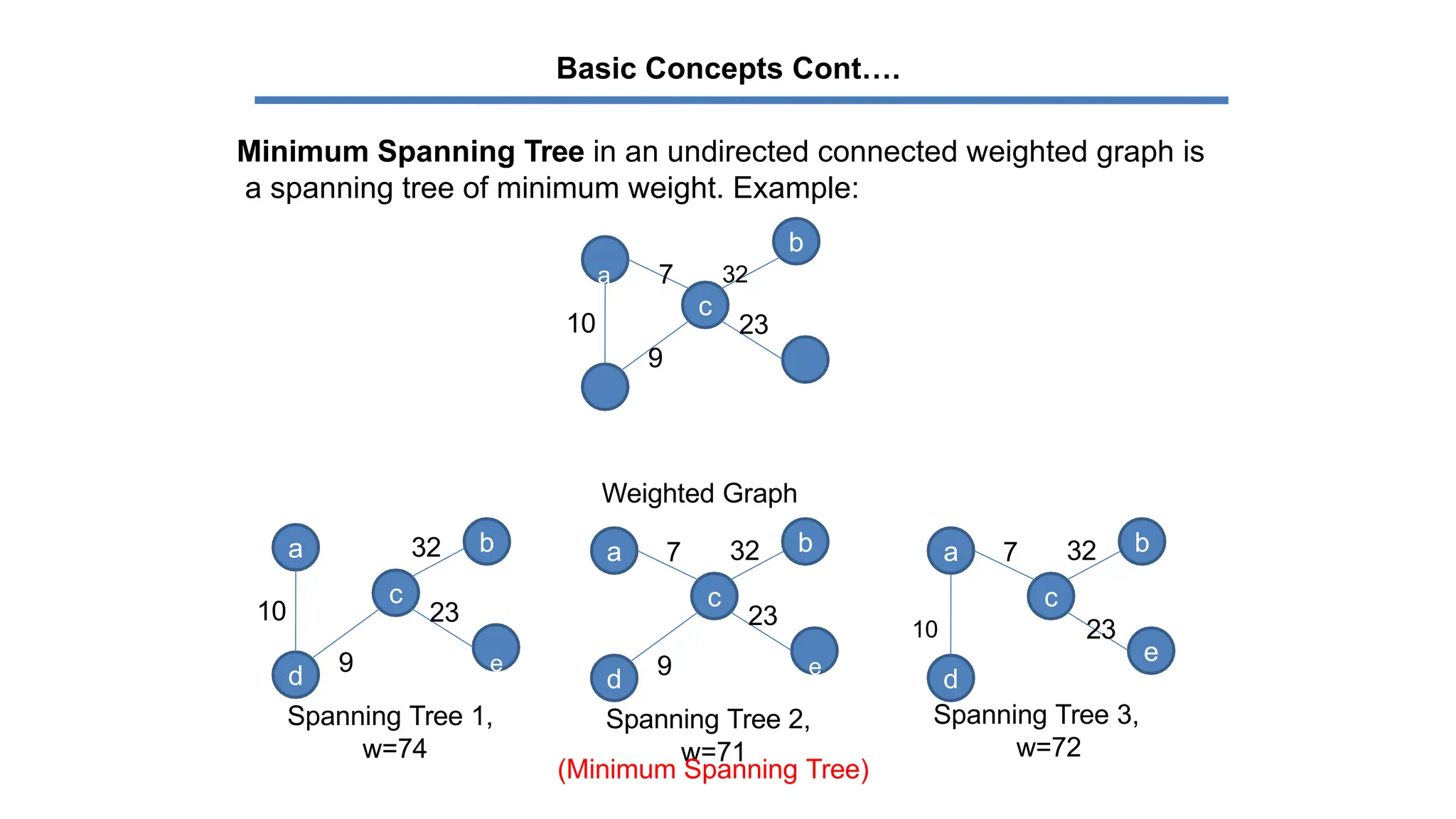
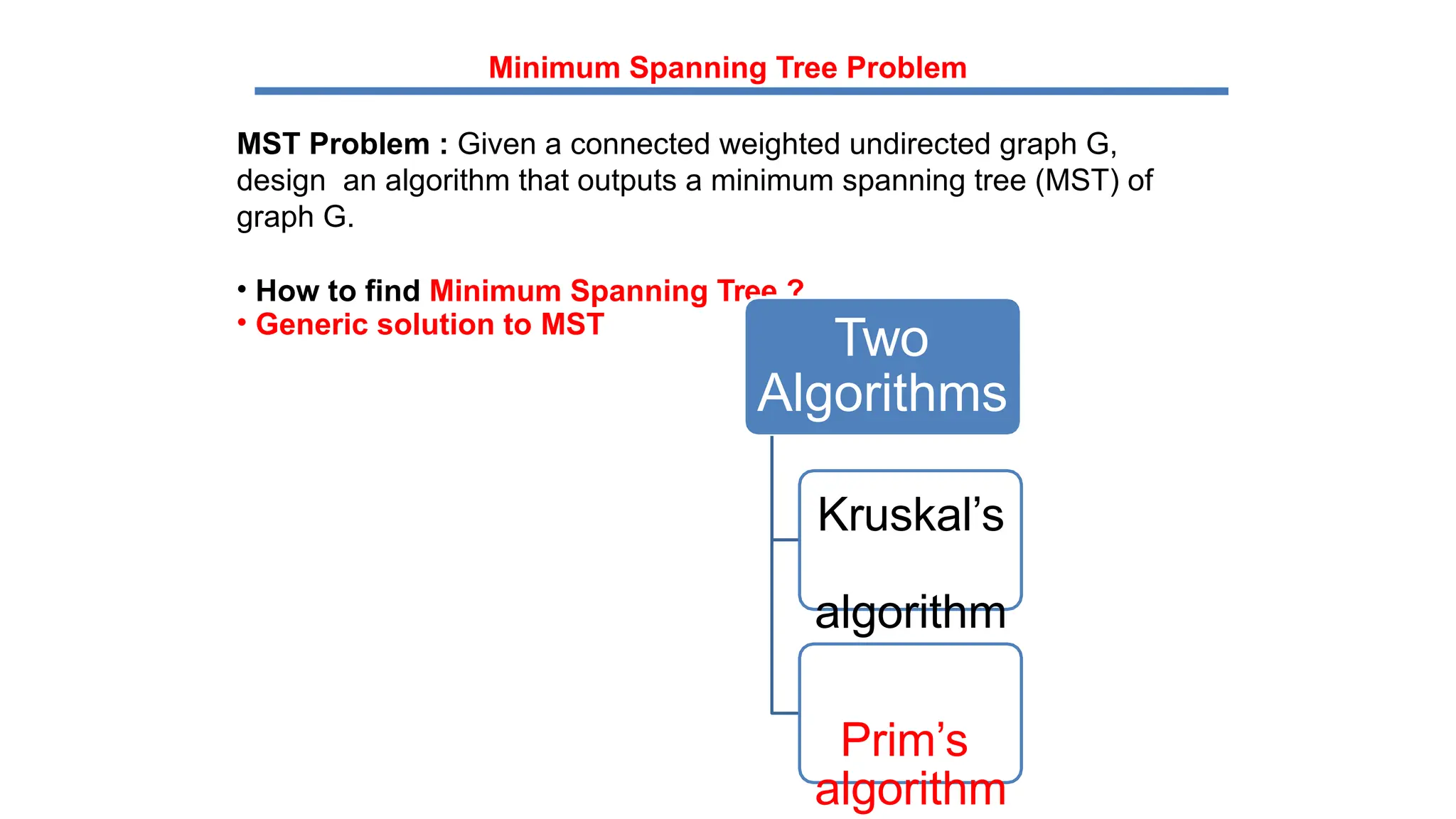
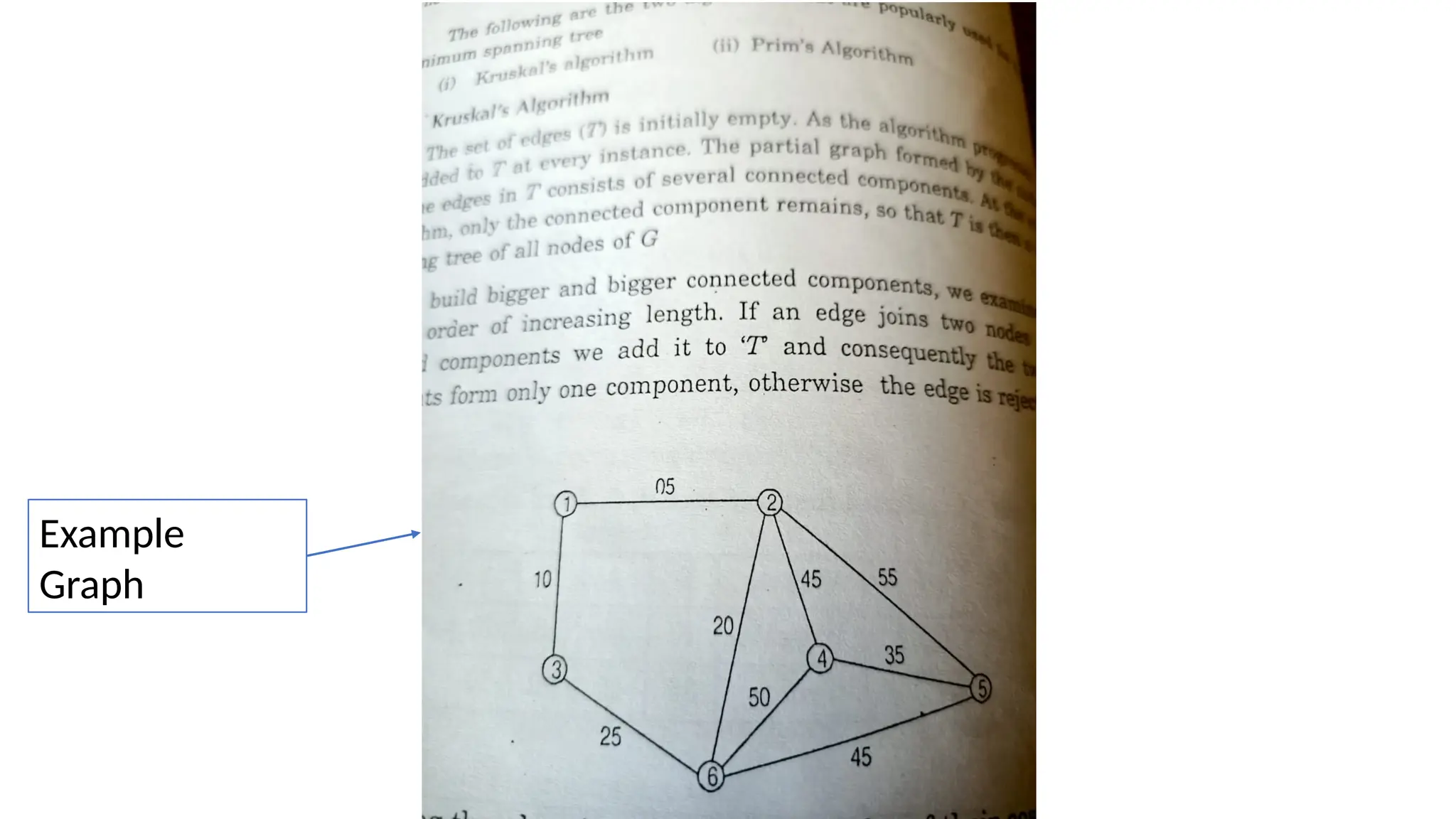
The document explains the greedy algorithm, which solves problems by making the locally optimal choice at each step, aiming for a globally optimal solution. It discusses spanning trees and minimum spanning trees (MST), including concepts like weighted graphs and algorithms such as Kruskal's and Prim's for finding MSTs. Various applications of MSTs are highlighted, including communication networks, transportation, and utility services.










![Step Edge Considered Connected
component
Graph
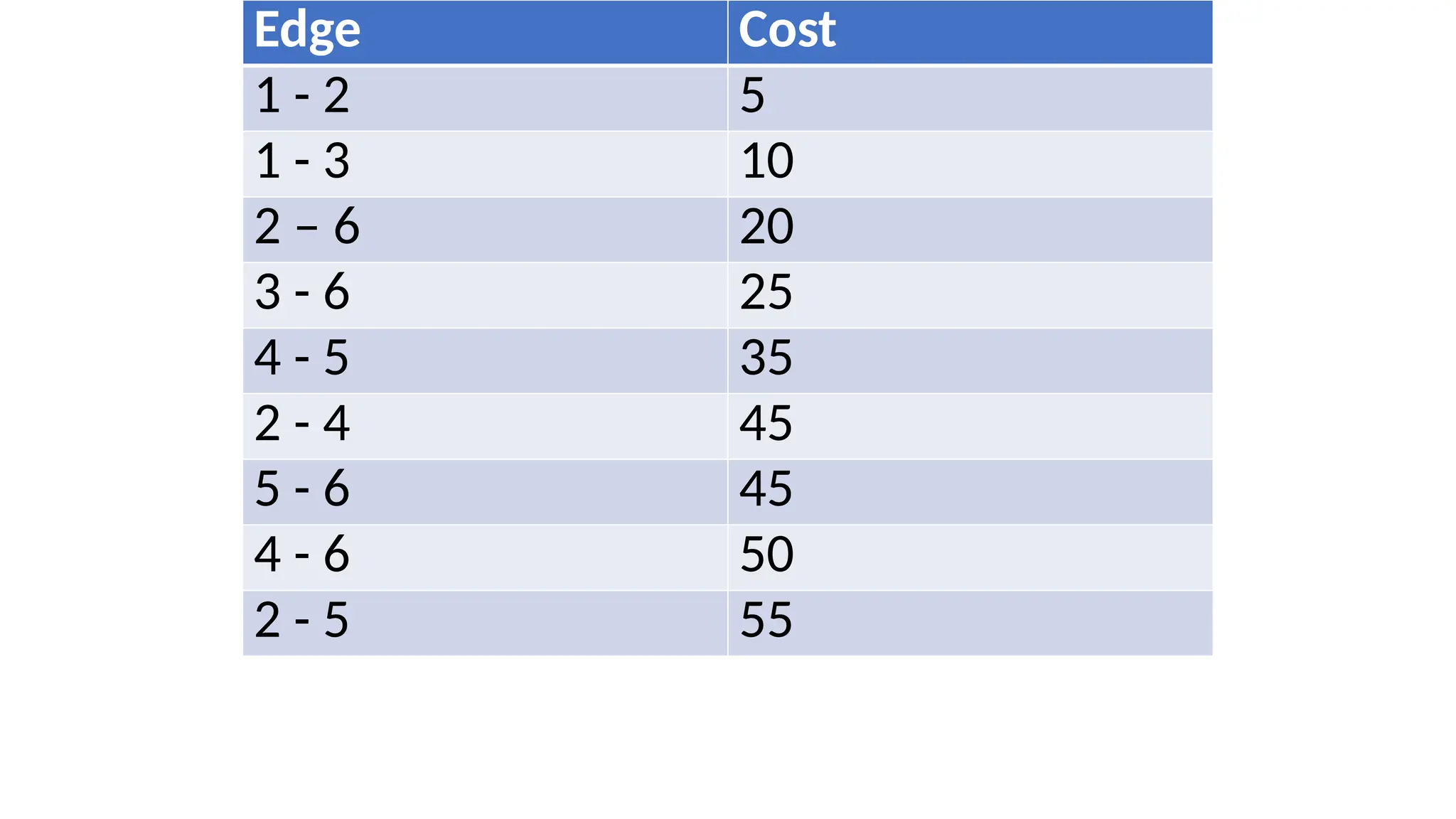
Initial - [1] [2] [3] [4] [5] [6] -
1. [1 – 2] [12] [3] [4] [5] [6]
Accepted because
no cycle
2. [1 – 3] [1 2 3] [4] [5] [6]
Accepted because
no cycle
1 2
5
1 2
3
5
10](https://image.slidesharecdn.com/kruskalsalgorithm1-250210161735-103cf03c/75/Data-Structures-and-Algorithms-Kruskals-algorithm-17-2048.jpg)
![Step Edge Considered Connected
Component
Graph
3. [2 – 6] [1 2 3 6] [4] [5]
Accepted because
no cycle
4. [3 – 6] Rejected because it
forms a cycle
-
5. [4 – 5] [1 2 3 6] [4 5]
Accepted because
no cycle
1 2
3
6
5
10
20
1 2
3
4 5
5
10 20 35](https://image.slidesharecdn.com/kruskalsalgorithm1-250210161735-103cf03c/75/Data-Structures-and-Algorithms-Kruskals-algorithm-18-2048.jpg)
![Step Edge Considered Connected
Component
Graph
6. [2 – 4] [1 2 3 4 5 6]
Accepted because no
cycle
7. [5 – 6] rejected -
8. [4 – 6] rejected
5
10
20
45
35](https://image.slidesharecdn.com/kruskalsalgorithm1-250210161735-103cf03c/75/Data-Structures-and-Algorithms-Kruskals-algorithm-19-2048.jpg)
![Step Edge
Considered
Connected
Component
Graph
8. [4 - 6] Rejected -
9. [2 – 5] Rejected -](https://image.slidesharecdn.com/kruskalsalgorithm1-250210161735-103cf03c/75/Data-Structures-and-Algorithms-Kruskals-algorithm-20-2048.jpg)
