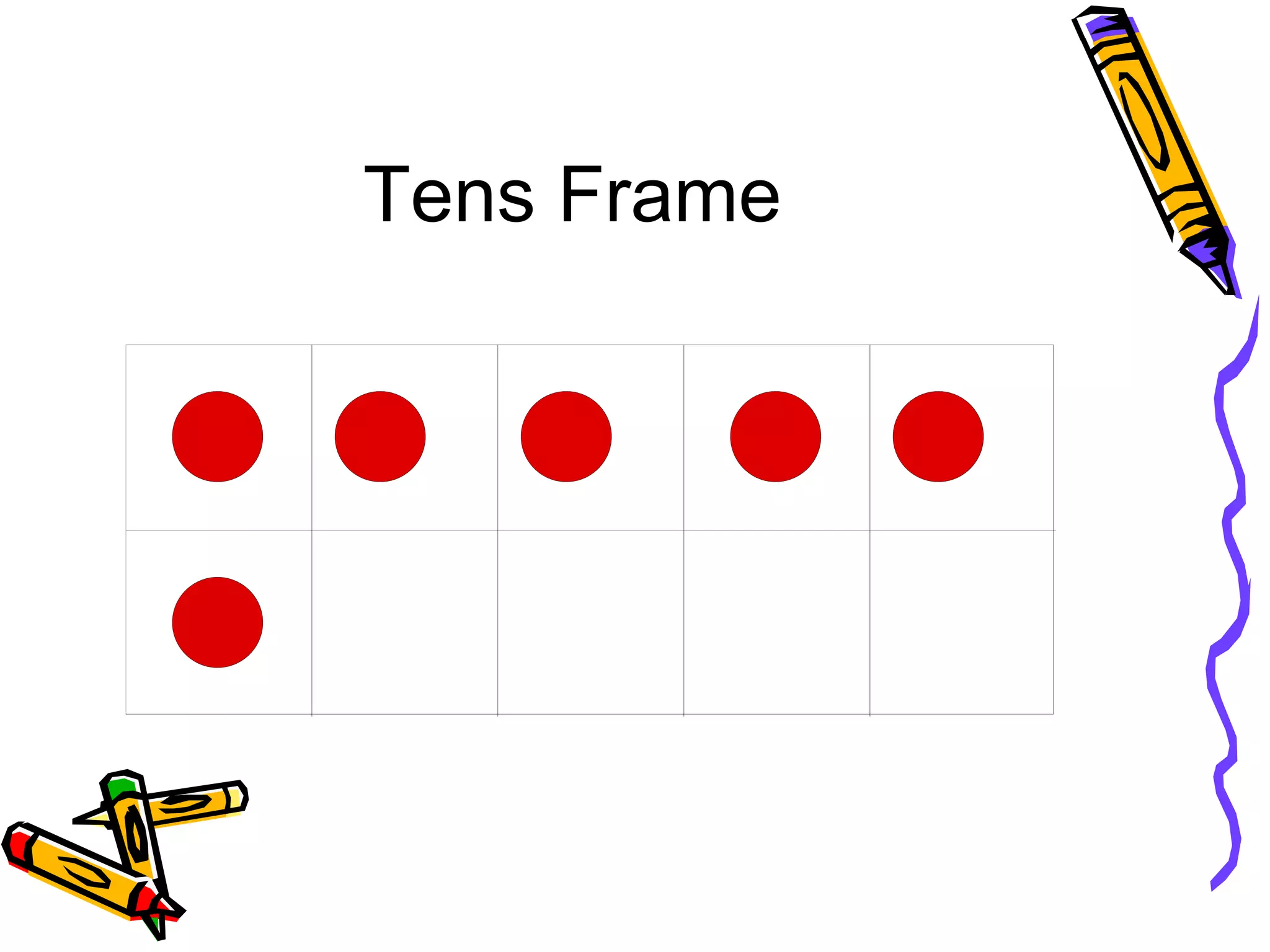
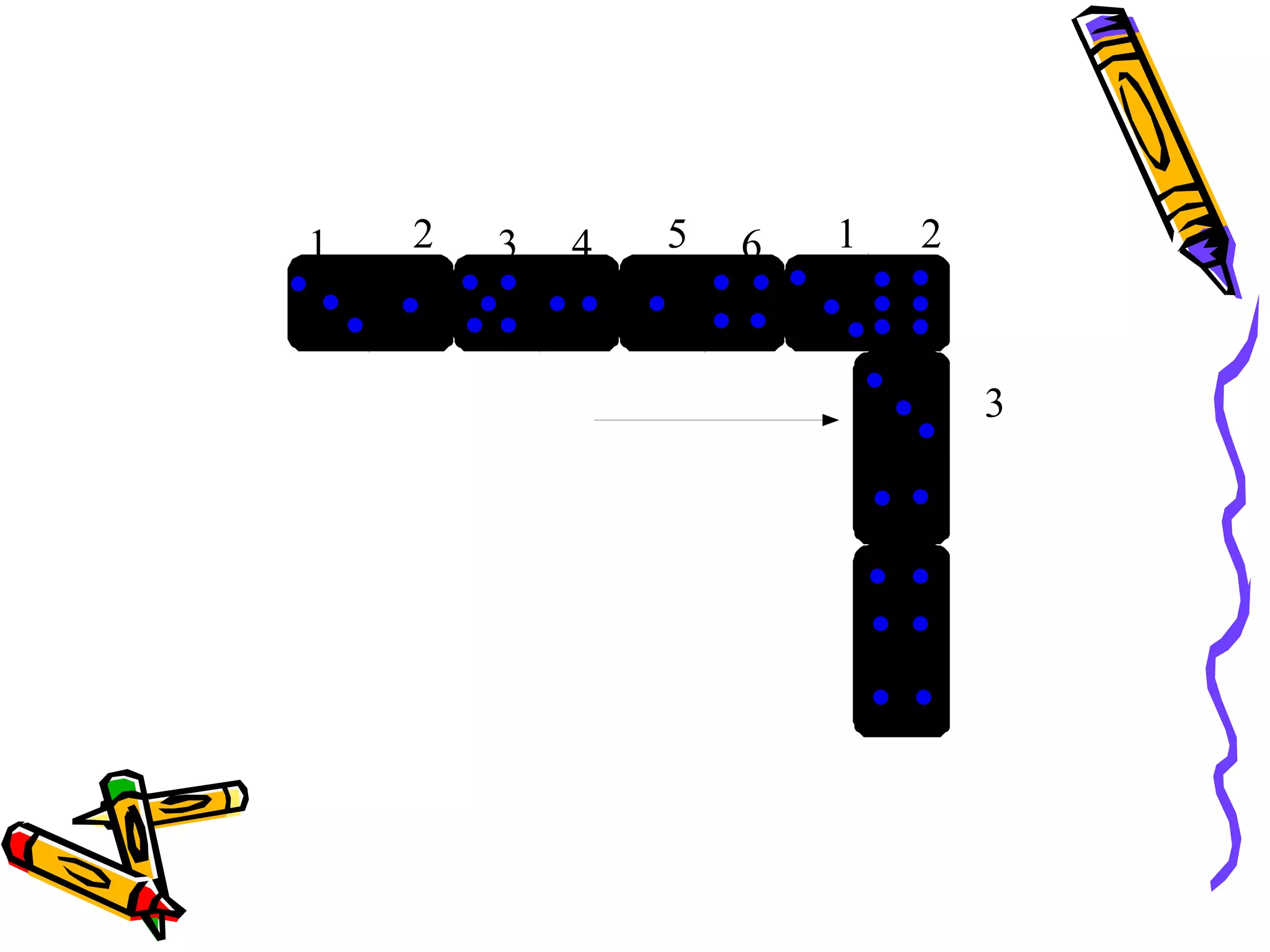
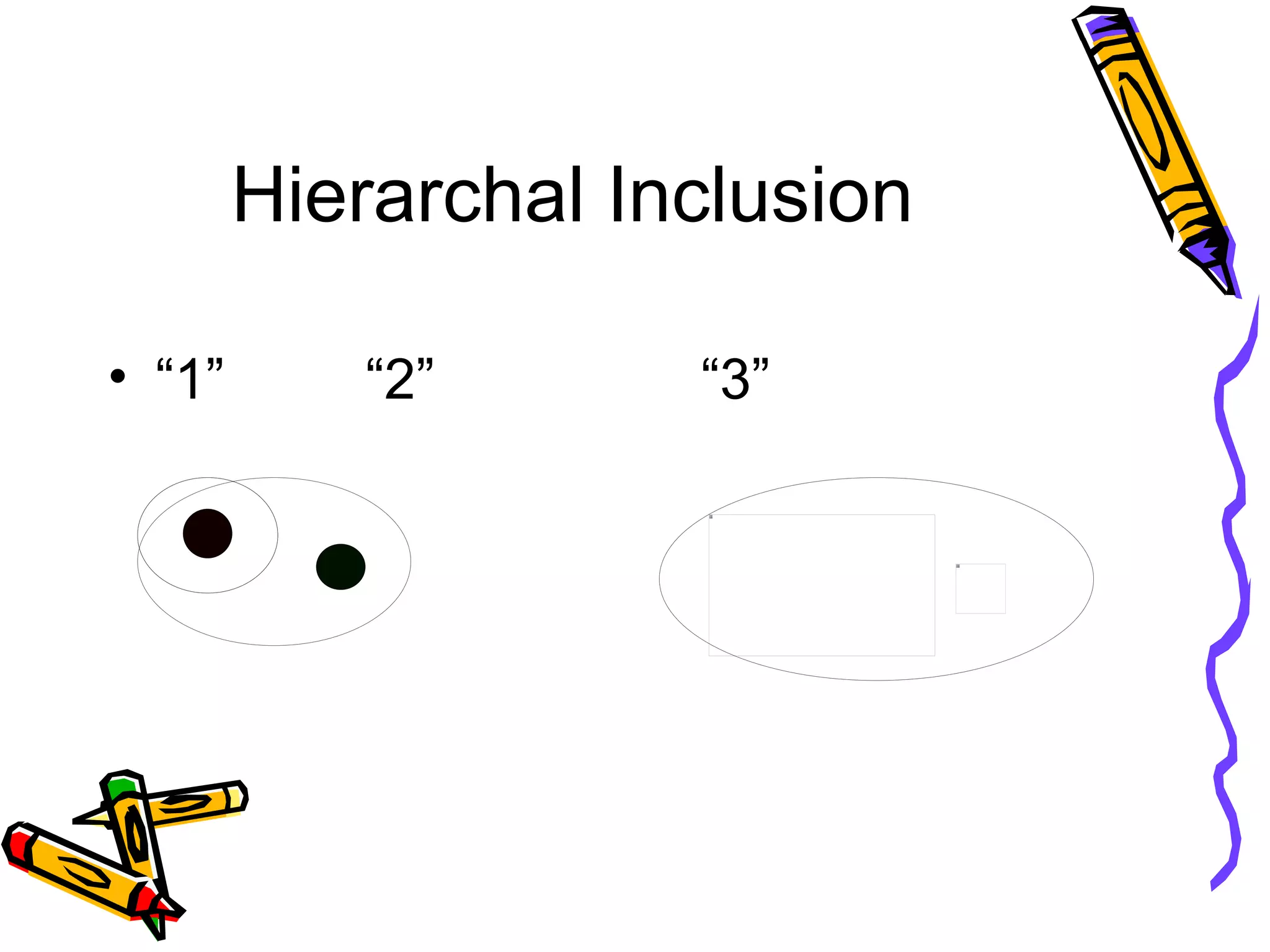
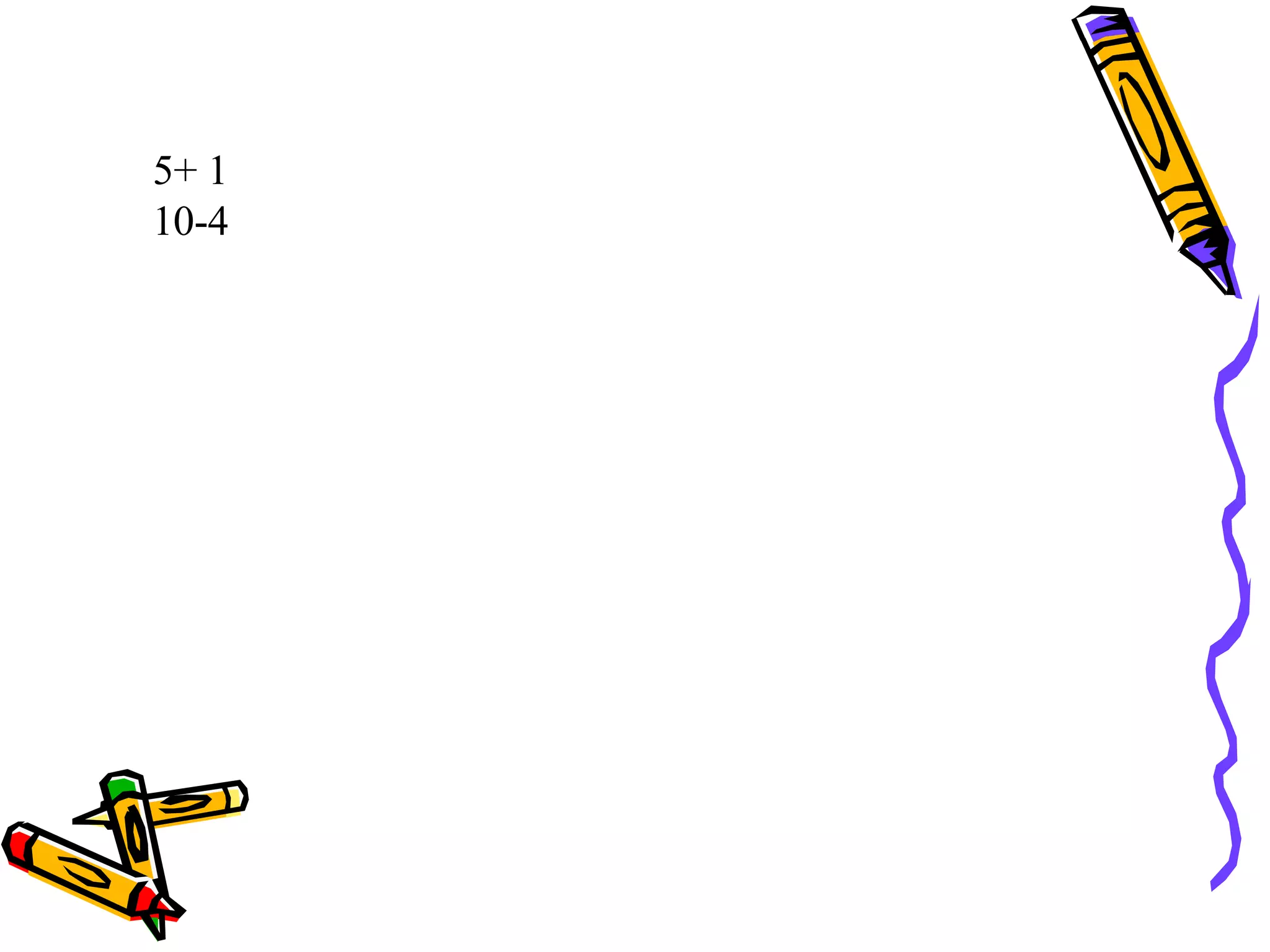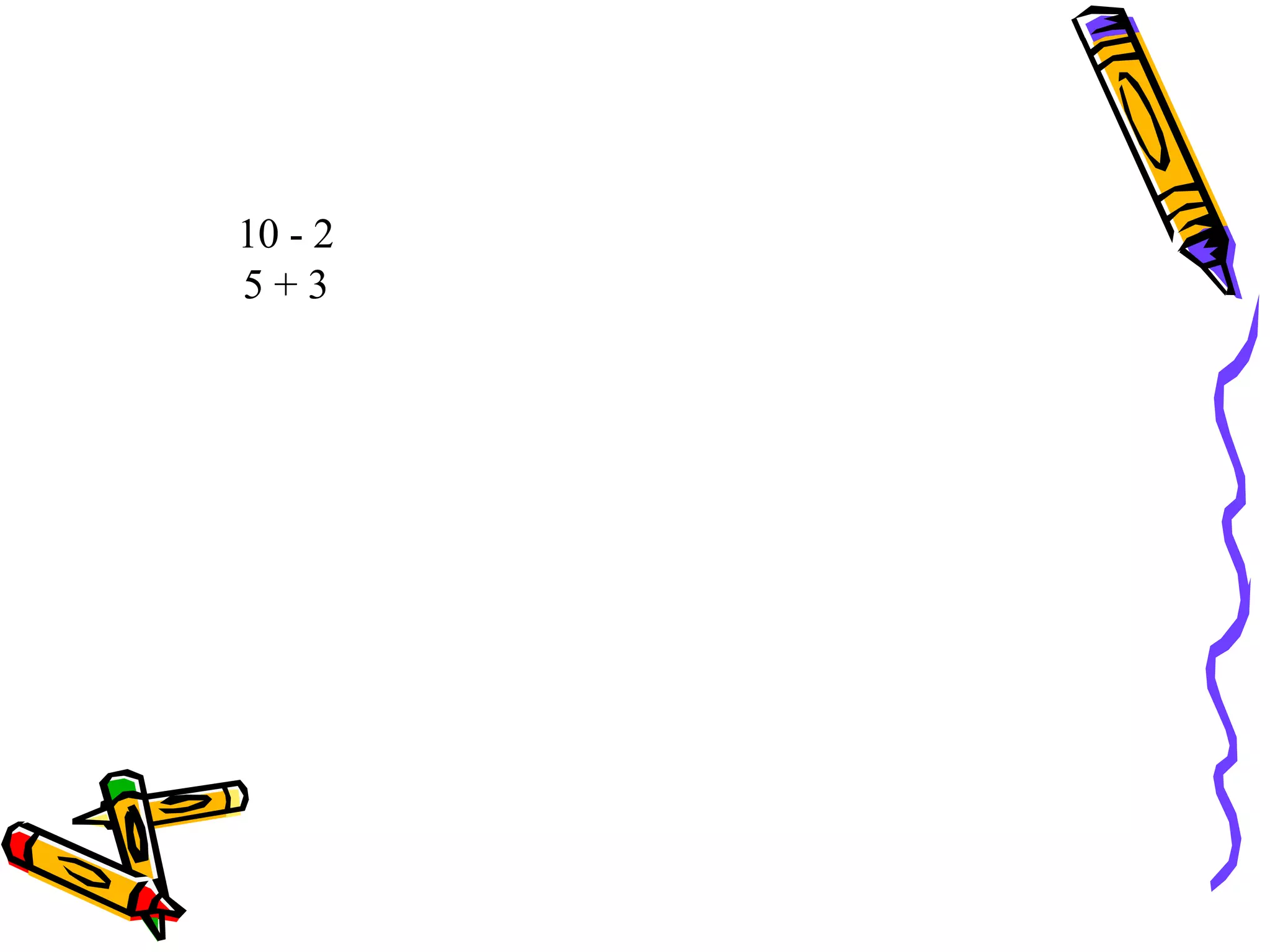This document discusses developing number sense in students and outlines several key building blocks or components of number sense, including rote counting, one-to-one correspondence, subitizing, tens frames, keeping track, conservation of number, hierarchical inclusion, compensation, part-whole relationships, unitizing/place value, and relationships between operations. It provides definitions and examples for each concept and suggests they take time and experience to build. A numerically powerful child can decompose numbers flexibly, understand relationships between numbers and operations, and connect numerals to real-life situations.
![Developing and Assessing Number Sense By Michelle Flaming [email_address]](https://image.slidesharecdn.com/developing-number-concepts-in-k2-learners-3295/75/Developing-Number-Concepts-in-K-2-Learners-1-2048.jpg)