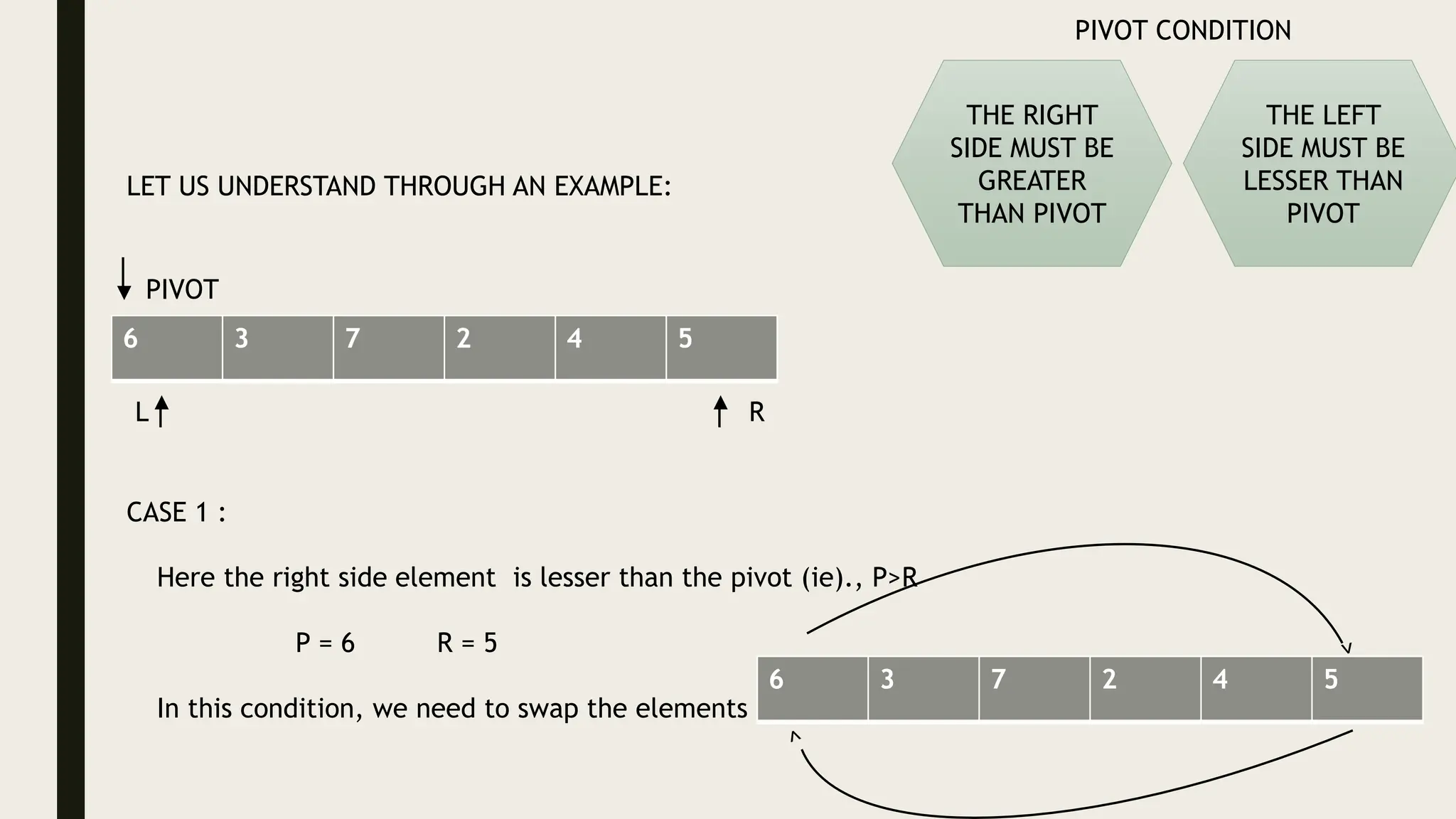
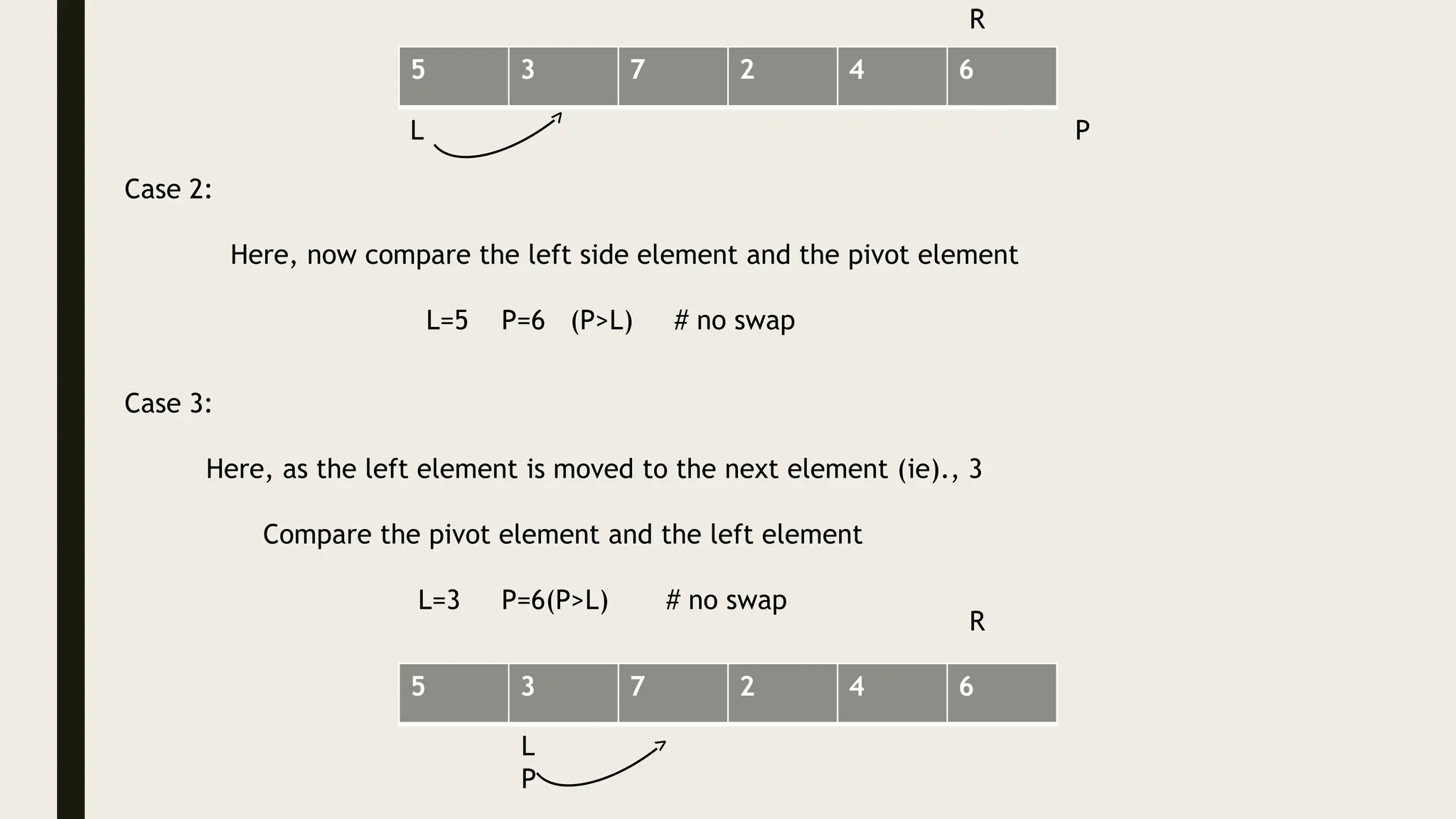
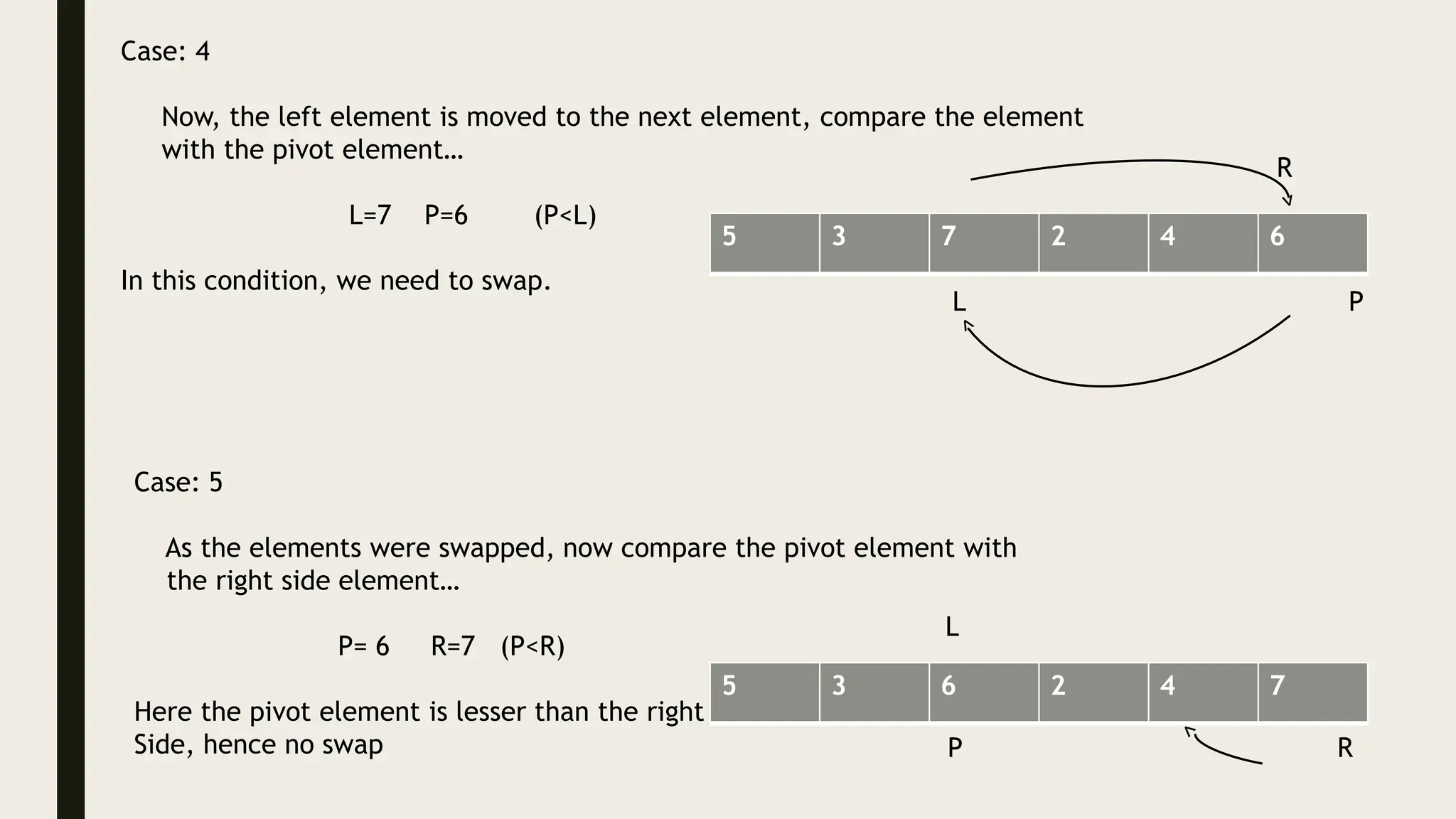
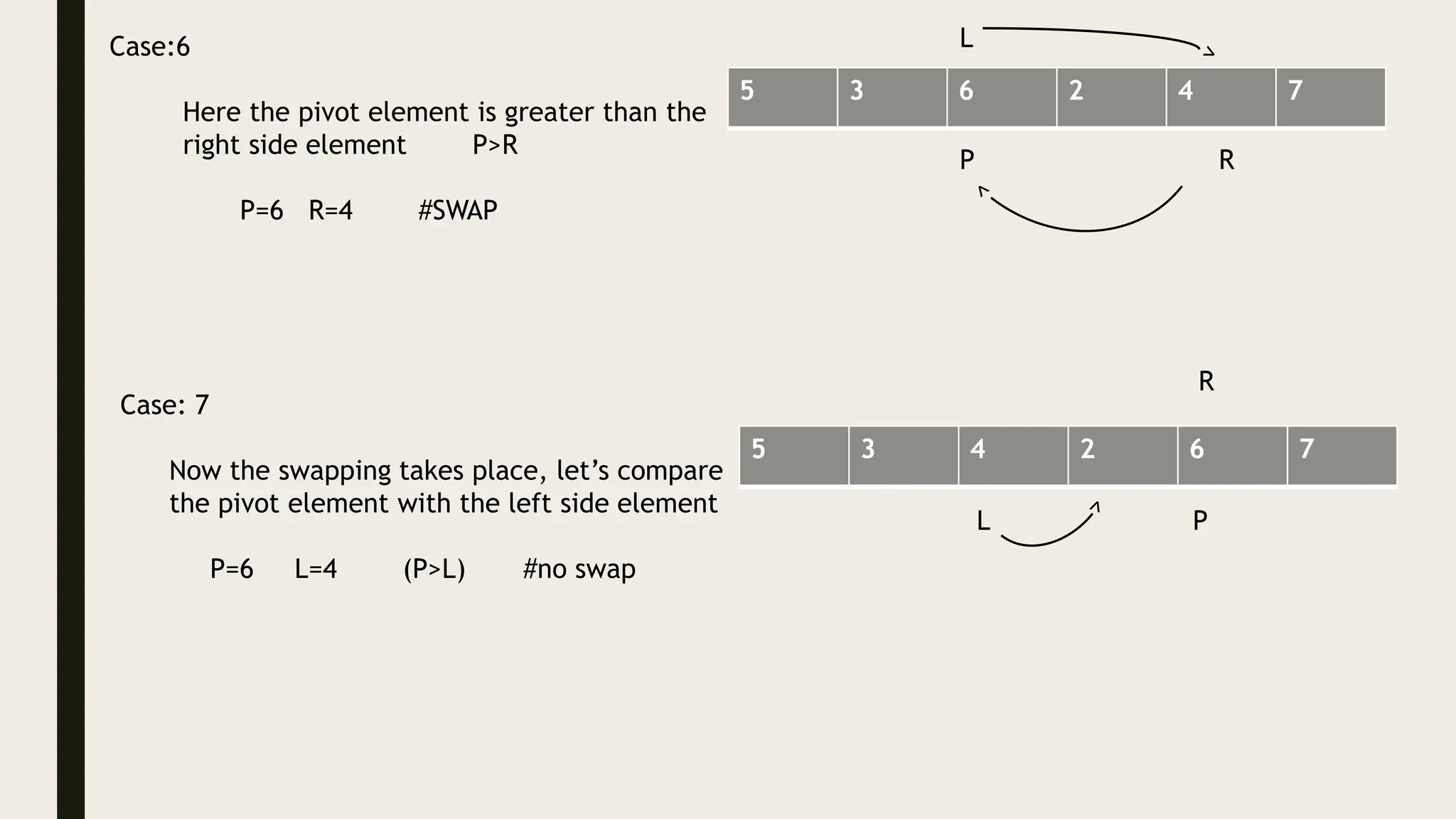
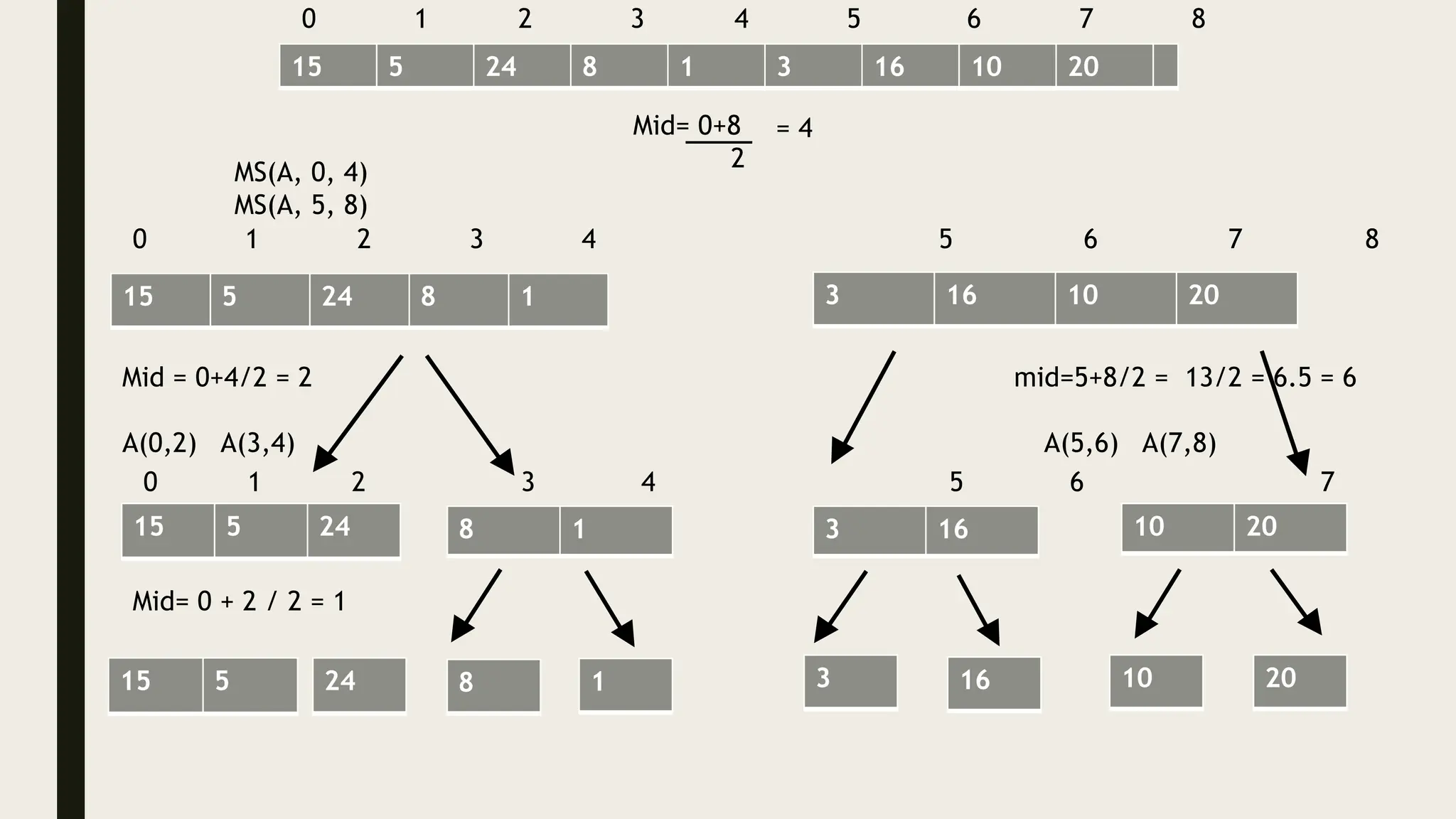
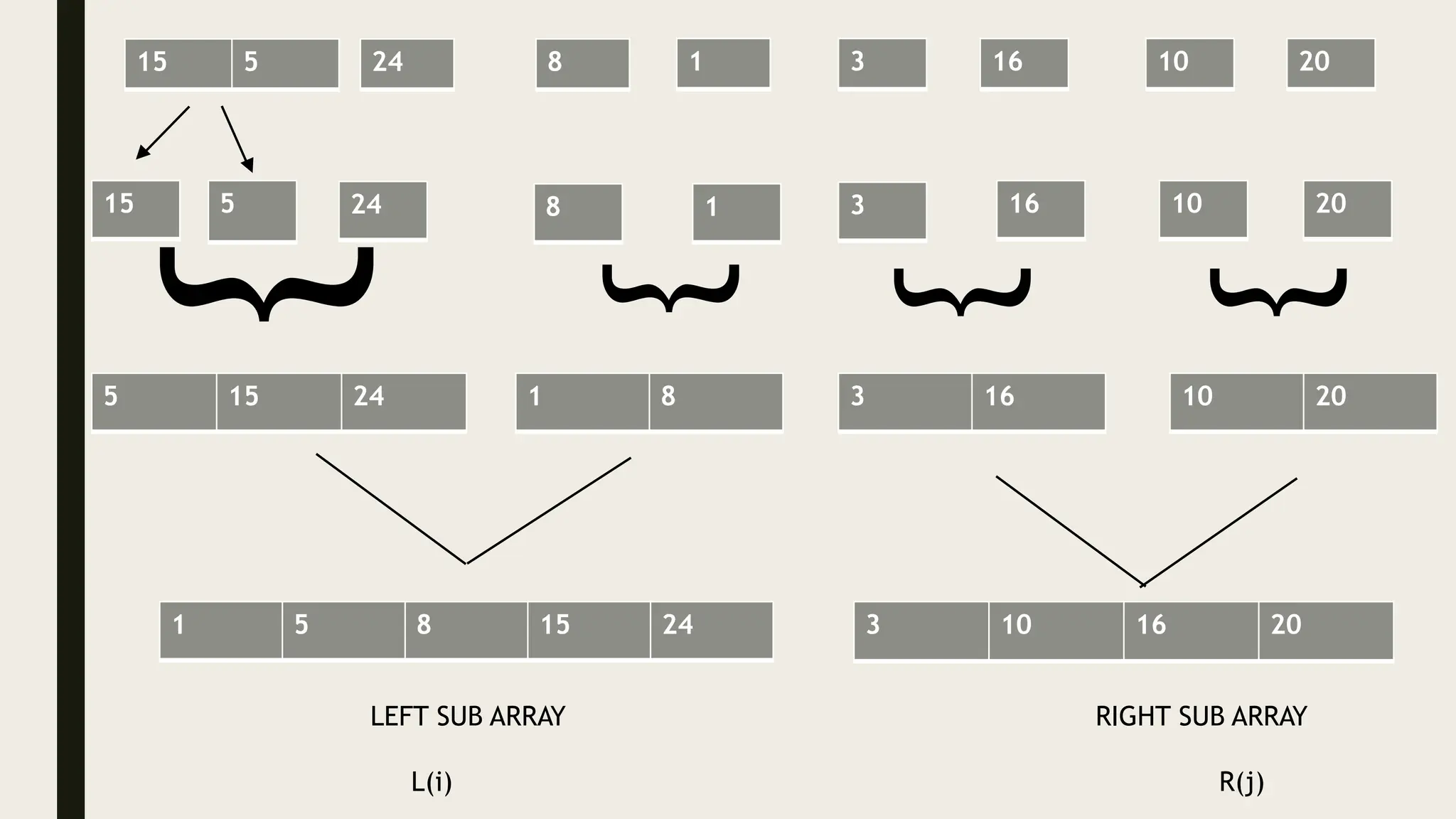
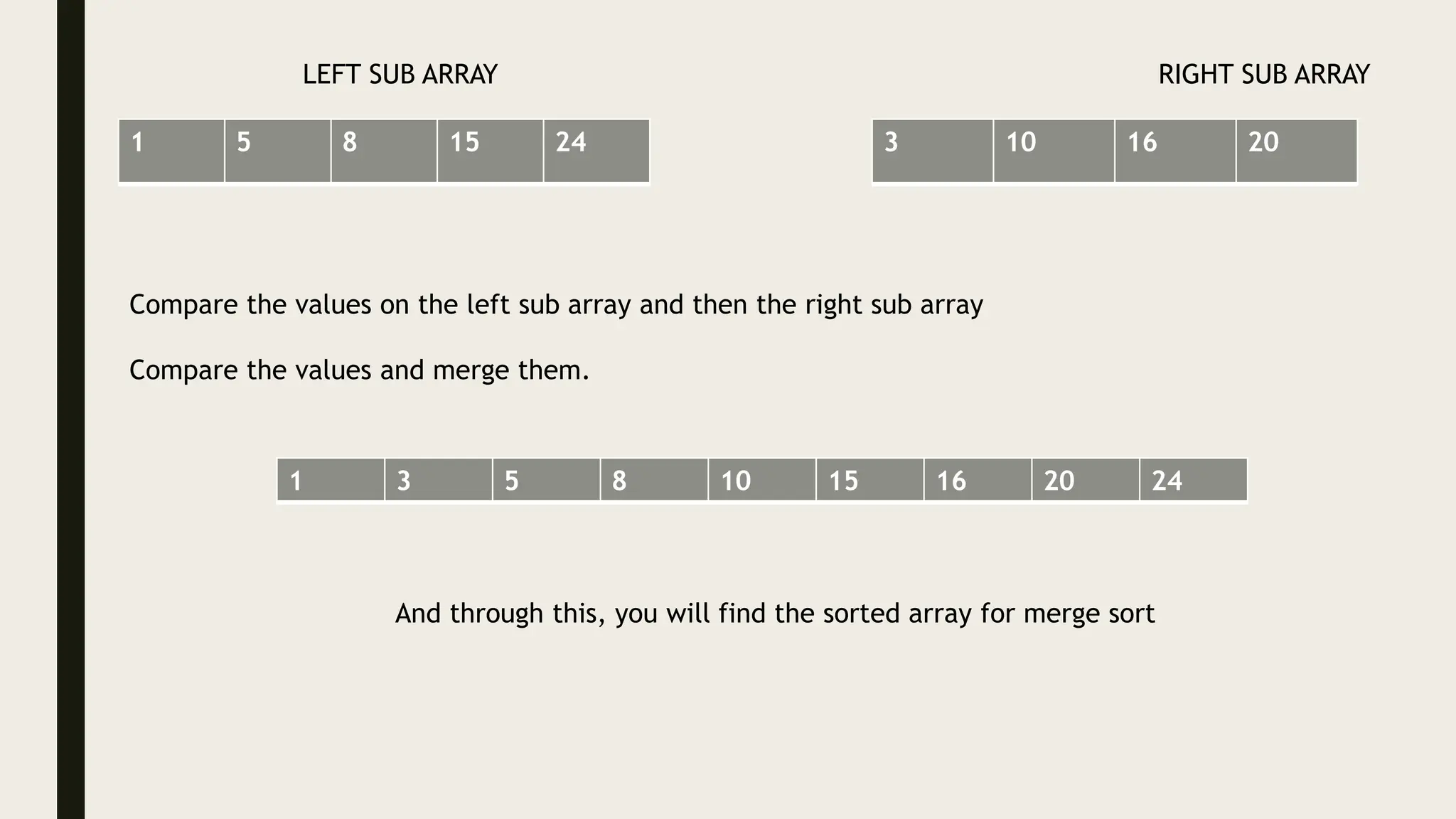
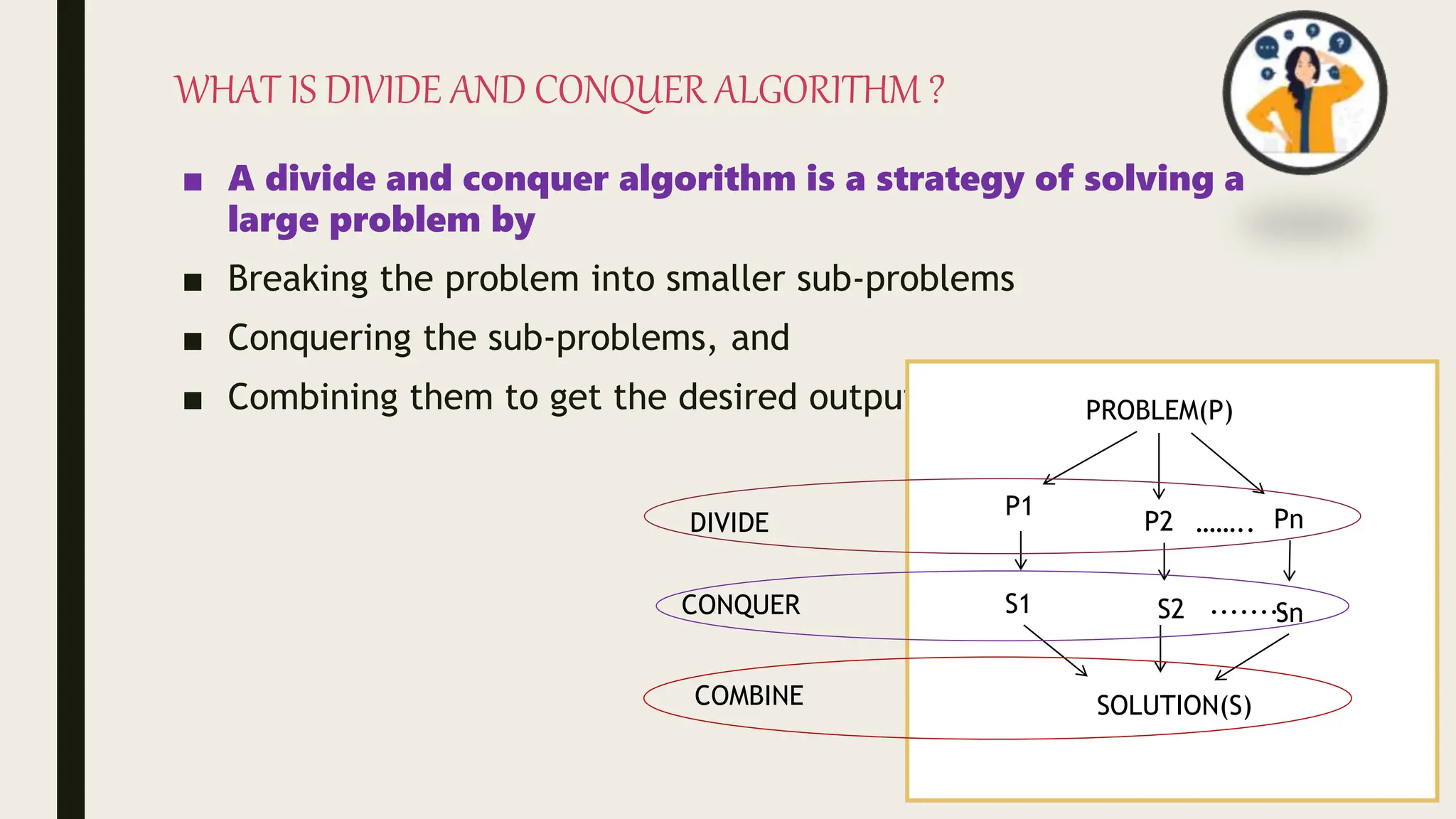
The document discusses the divide and conquer algorithm and provides examples of algorithms that use this approach, including merge sort, quicksort, and binary search. It explains that divide and conquer works by dividing a problem into smaller subproblems, solving those subproblems recursively, and then combining the solutions to solve the original problem. Specific steps and pseudocode are provided for merge sort, quicksort, and binary search to illustrate how they apply the divide and conquer strategy.




![ALGORITHM FOR BINARY SEARCH
binarysearch(a, n, key)
start=0, end= n-1
while(start<=end)
{
mid=start+end ;
2
if(key==a[mid])
return mid;
else if(key<a[mid])
end=mid-1;
else
start=mid+1;
} #end of loop
return -1; #start>end
} unsuccessful search](https://image.slidesharecdn.com/dividendconquer-240402053929-42f94b95/75/DIVIDE-AND-CONQUERMETHOD-IN-DATASTRUCTURE-pptx-7-2048.jpg)
![5 9 17 23 25 45 59 63 71 89
0 1 2 3 4 5 6 7 8 9
start end
KEY=59 #element to be found
m=10
EXAMPLE OF BINARY SEARCH
mid=start+end
2
=0+9/2
=4.5 => 4
So the mid value is 4
a[mid] = a[4] = 25](https://image.slidesharecdn.com/dividendconquer-240402053929-42f94b95/75/DIVIDE-AND-CONQUERMETHOD-IN-DATASTRUCTURE-pptx-8-2048.jpg)
![KEY= MID
KEY< MID -> END=MID-1
KEY>MID -> START=MID+1
And here now, as the key value is greater than the mid value,
Start = mid +1
= 4 +1
= 5
59>25
45 59 63 71 89
5 6 7 8 9
Start End
Mid = start + end = 5+9 = 14 = 7
2 2 2
a[mid]= 7 = 63](https://image.slidesharecdn.com/dividendconquer-240402053929-42f94b95/75/DIVIDE-AND-CONQUERMETHOD-IN-DATASTRUCTURE-pptx-9-2048.jpg)
![Here the key value is lesser than the mid value,
end = mid – 1
= 7 - 1
= 6
59<63
45 59
5 6
Start end
Mid= 5+6/2 = 11/2 = 5.5 = 5
a[mid]=45](https://image.slidesharecdn.com/dividendconquer-240402053929-42f94b95/75/DIVIDE-AND-CONQUERMETHOD-IN-DATASTRUCTURE-pptx-10-2048.jpg)
![Now the mid value is lesser than the key value,
Start= mid+ 1
= 5 + 1
= 6
45<59
59
6
Start end
Mid = 6 + 6
2
= 6 a[mid] = a[6] = 59
As key = mid
return mid
FINALLY THE KEY VALUE IS FOUND USING BINARY SEARCH](https://image.slidesharecdn.com/dividendconquer-240402053929-42f94b95/75/DIVIDE-AND-CONQUERMETHOD-IN-DATASTRUCTURE-pptx-11-2048.jpg)