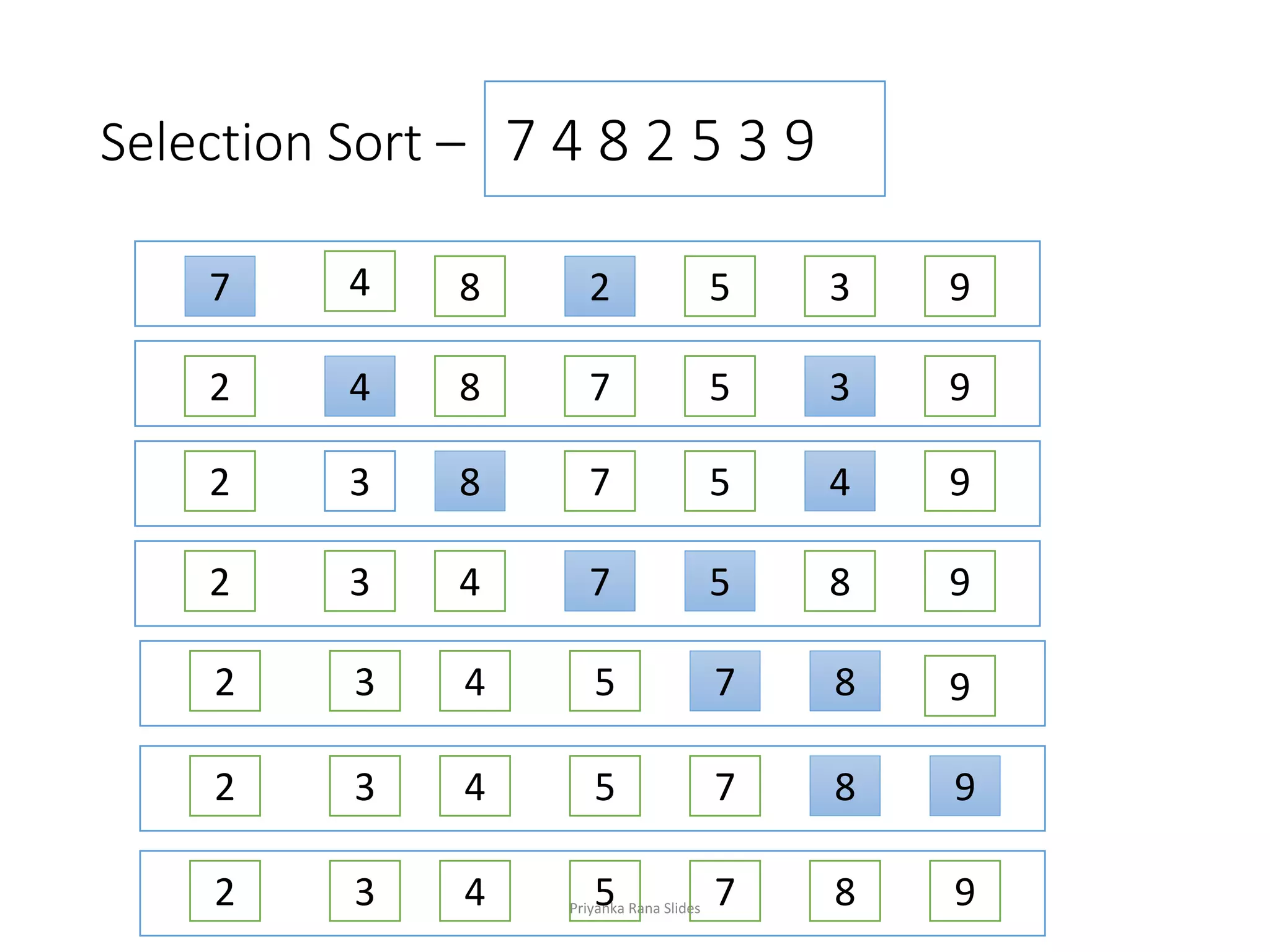
The document discusses sorting algorithms, specifically insertion and selection sort, utilizing priority queues. It details the performance of these algorithms with unsorted and sorted lists, noting the time complexities for insertion and removal operations. Finally, it outlines the sequential steps and running times of sorting various input sequences using priority queues.