Introduction to Monads in Scala (2)

Monads

Part 2
functional programming with scala

Choose your…

• DSL
• Actors
• OOP
• Procedures
• Functional

public class VersionFormatter {
private final String comp;

public VersionFormatter(String comp) {
this.comp = comp;
}

public String generate(String app) {
return ”{" + comp + " - " + app + “}";
}
}

VersionFormatter myCompFormat = new VersionFormatter("Co");
System.out.println(myCompFormat.generate("App"));

case class VersionFormatter(val comp: String) {
def generateFor(app: String): String = ”{" + comp + " - " + app + “}"
}

val myCompFormat = VersionFormatter("Co")
println(myCompFormat generateFor "App")

def generate(comp: String, app: String) = ”{%s - %s}".format(comp, app)

val myCompFormat = generate ("Co", _: String)
println(myCompFormat("App"))

Examples
return output filterById map toJson

ls | grep '^d'

val service = {
path("orders") {
authenticate(httpBasic(realm = "admin area")) { user =>
get {
cacheResults(LruCache(maxCapacity = 1000, timeToIdle =
Some(30.minutes))) {
encodeResponse(Deflate) {
completeWith {
// marshal custom object with in-scope // marshaller
getOrdersFromDB
}
}
}
}~

var avg: Option[Float] =
from(grades)(g =>
where(g.subjectId === mathId)
compute(avg(
g.scoreInPercentage))
)

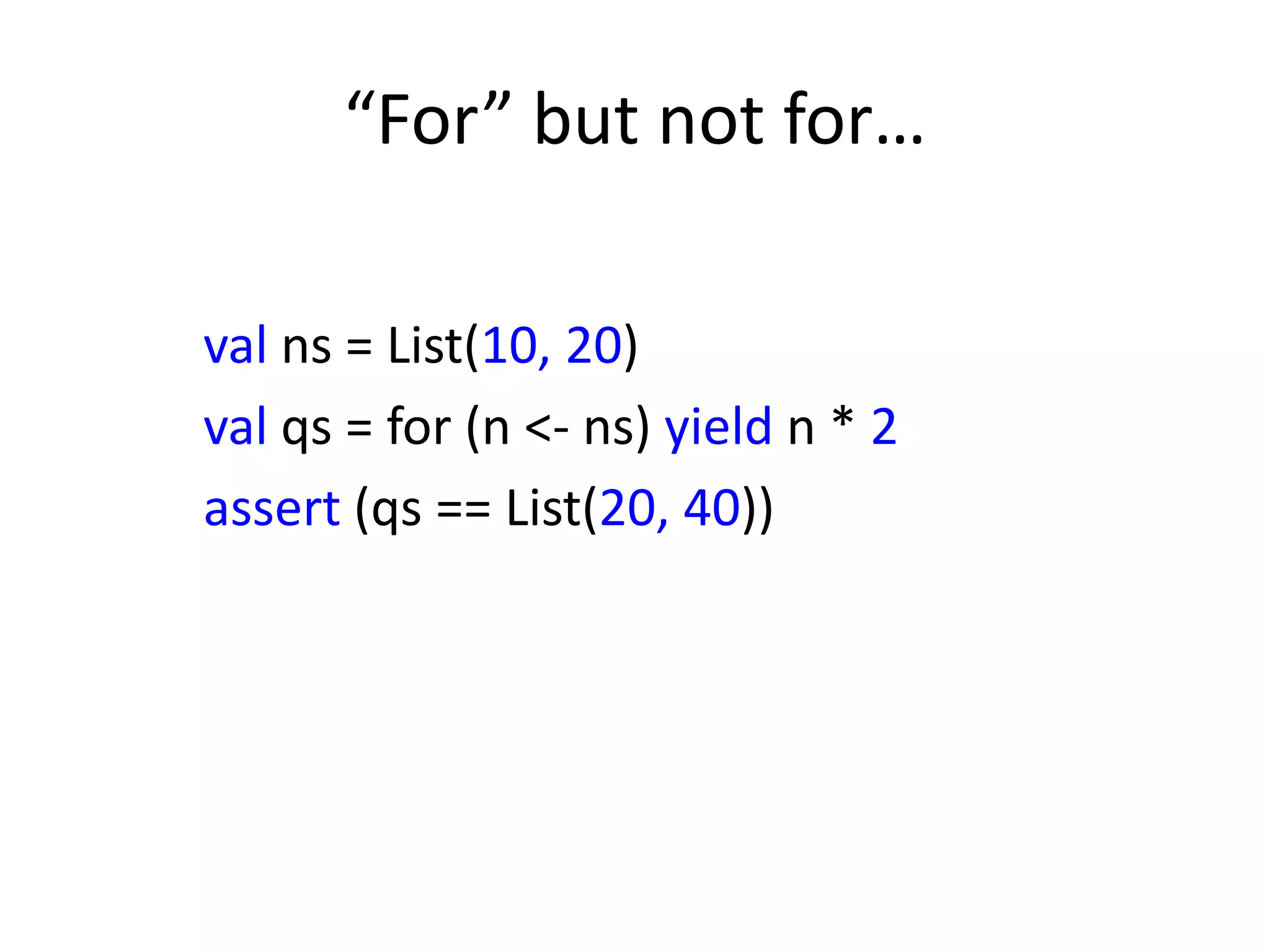
“For” but not for…

val ns = List(10, 20)
val qs = for (n <- ns) yield n * 2
assert (qs == List(20, 40))

Map like for
val ns = List(10, 20)

val qs = ns map {n => n * 2}

For like map

for (x <- expr) yield resultExpr
=
expr map {x => resultExpr}
=
expr flatMap {x => unit(resultExpr)}

for [each] n [in] ns [and each] o [in] os
yield n * o
val in1 = List(1, 2)
val in2 = List (3, 4)
val out = for (n <- in1; o <- in2) yield n + o
assert (out == List (1+3, 1+4, 2+3, 2+4))
=
val out2 = in1 flatMap {n =>
in2 map {o => n + o }}
assert(out == out2)

Step by step
val out = ns flatMap {n => os map {o => n + o }}

val qs = ns flatMap {n => List(n + 3, n + 4)}

val qs = List(1 + 3, 1 + 4, 2 + 3, 2 + 4)

More of For…
val out = for (n <- in1; o <- in2; p <- in3)
yield n + o + p

val qs = ns flatMap {n =>
os flatMap {o =>
{ps map {p => n + o + p}}}}

rule is recursive
For (x1 <- expr1;...x <- expr)
yield resultExpr

=
expr1 flatMap {x1 =>
for(...;x <- expr) yield resultExpr
}

Imperative "For"
Just loosing yield:

val ns = List(1, 2)
val os = List (3, 4)
for (n <- ns; o <- os) println(n + o)
=
ns foreach {n => os foreach {o => println(n + o) }}

Foreach is imperative form of "for"
class M[A] {
def map[B](f: A=> B) : M[B] = ...
def flatMap[B](f: A => M[B]) : M[B] = ...
def foreach[B](f: A=> B) : Unit = {
map(f)
return ()
}
}

Filtering
val names = List ( “Mike”, “Raph”, “Don”, “Leo” )
val eNames = for (eName <- names;
if eName.contains ( ‘e’ )
) yield eName + “ is a name contains e”

assert(eNames == List(
"Mike is a name contains e",
"Leo is a name contains e"))

Filtering with map
val bNames =
(names filter { eName => eName.contains('e') })
.map { eName => eName + " is a name
contains e"
}

Basis 2
Haskell Scala
do var1<- expn1 for {var1 <- expn1;
var2 <- expn2 var2 <- expn2;
expn3 result <- expn3
} yield result
do var1 <- expn1 for {var1 <- expn1;
var2 <- expn2 var2 <- expn2;
return expn3 } yield expn3
do var1 <- expn1 >> expn2 for {_ <- expn1;
return expn3 var1 <- expn2
} yield expn3

Setting the Law

f(x) ≡ g(x)

But no eq, ==, hashCode, ref
All the laws I present implicitly assume that
there are no side effects.

Breaking the law
Mathematic example:
a*1≡a
a*b≡b*a
(a * b) * c ≡ a * (b * c)

WTF - What The Functor?
In Scala a functor is a class with a map method
and a few simple properties.
class M[A] {
def map[B](f: A => B):M[B] = ...
}

First Functor Law: Identity
def identity[A](x:A) = x
identity(x) ≡ x

So here's our first functor law: for any functor m
– F1. m map identity ≡ m // or equivalently *
– F1b. m map {x => identity(x)} ≡ m // or
equivalently
– F1c. m map {x => x} ≡ m

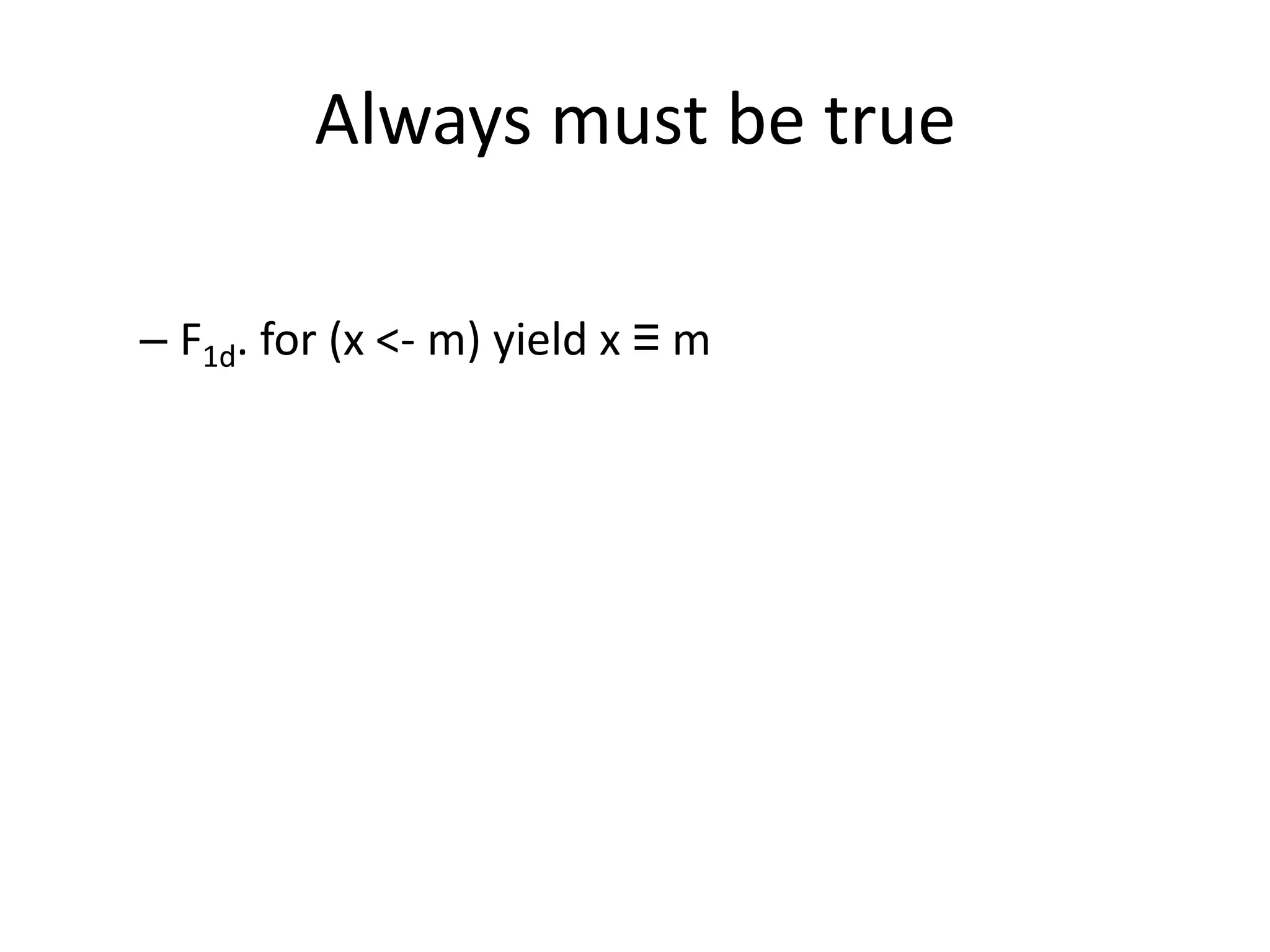
Always must be true

– F1d. for (x <- m) yield x ≡ m

Second Functor Law: Composition

F2. m map g map f ≡ m map {x => f(g(x))}

Always must work
val result1 = m map (f compose g)
val temp = m map g
val result2 = temp map f
assert result1 == result2

For analogue

F2b. for (y<- (for (x <-m) yield g(x)) yield f(y) ≡
for (x <- m) yield f(g(x))

Functors and Monads
All Monads are Functors

class M[A] {
def map[B](f: A => B):M[B] = ...
def flatMap[B](f: A=> M[B]): M[B] = ...
def unit[A](x:A):M[A] = …
}
Scala way for unit Object apply().

The Functor/Monad Connection Law
FM1. m map f ≡ m flatMap {x => unit(f(x))}

Three concepts: unit, map, and flatMap.

FM1a. for (x <- m) yield f(x) ≡ for (x <- m; y <-
unit(f(x))) yield y

Flatten in details
FL1. m flatMap f ≡ flatten(m map f)
=
1. flatten(m map identity) ≡ m flatMap identity
// substitute identity for f
2. FL1a. flatten(m) ≡ m flatMap identity // by F1

The First Monad Law: Identity
1. M1. m flatMap unit ≡ m // or equivalently
2. M1a. m flatMap {x => unit(x)} ≡ m

Where the connector law connected 3 concepts,
this law focuses on the relationship between 2
of them

Identity
• m flatMap {x => unit(x)} ≡ m // M1a
• m flatMap {x => unit(identity(x))}≡ m //
identity
• F1b. m map {x => identity(x)} ≡ m // by FM1
• M1c. for (x <- m; y <- unit(x)) yield y ≡ m

The Second Monad Law: Unit
• M2. unit(x) flatMap f ≡ f(x) // or equivalently
• M2a. unit(x) flatMap {y => f(y)} ≡ f(x)
• M2b. for (y <- unit(x); result <- f(y)) yield result
≡ f(x)

It's in precisely this sense that it's safe to say
that any monad is a type of container (but that
doesn't mean a monad is a collection!).

Rephrasing
• unit(x) map f ≡ unit(x) map f // no, really, it
does!
• unit(x) map f ≡ unit(x) flatMap {y => unit(f(y))}
// by FM1
• M2c. unit(x) map f ≡ unit(f(x)) // by M2a
• M2d. for (y <- unit(x)) yield f(y) ≡ unit(f(x))

The Third Monad Law: Composition
• M3. m flatMap g flatMap f ≡
m flatMap {x => g(x) flatMap f} // or
equivalently
• M3a. m flatMap {x => g(x)} flatMap {y => f(y)} ≡
m flatMap {x => g(x) flatMap {y => f(y) }}

Mind breaker
• M3b.
for (a <- m; b <- g(a); result <- f(b) ) yield result ≡
for (a <- m; result <-
for(b < g(a); temp <- f(b) ) yield temp )
yield result

?
1. m map g map f ≡ m map g map f // is it?
2. m map g map f ≡ m flatMap {x => unit(g(x))} flatMap
{y => unit(f(y))} // by FM1, twice
3. m map g map f ≡ m flatMap {x => unit(g(x)) flatMap {y
=> unit(f(y))}} // by M3a
4. m map g map f ≡ m flatMap {x => unit(g(x)) map {y =>
f(y)}} // by FM1a
5. m map g map f ≡ m flatMap {x => unit(f(g(x))} // by
M2c
6. F2. m map g map f ≡ m map {x => f(g(x))} // by FM1a

Monadic zeros
Nill for List
None for Option

The First Zero Law: Identity
MZ1. mzero flatMap f ≡ mzero

1. mzero map f ≡ mzero map f // identity
2. mzero map f ≡ mzero flatMap {x => unit(f(x))
// by FM1
3. MZ1b. mzero map f ≡ mzero // by MZ1

Not enough zero
unit(null) map {x => "Nope, not empty enough
to be a zero"} ≡
unit("Nope, not empty enough to be a zero")

The Second Zero Law: M to Zero in
Nothing Flat
MZ2. m flatMap {x => mzero} ≡ mzero

Anything to nothing is nothing

What is +
Type Method
Int +
List :::
Option orElse

The Third and Fourth Zero Laws: Plus
class M[A] {
...
def plus(other:M[B >: A]): M[B] = ...
}

• MZ3. mzero plus m ≡ m
• MZ4. m plus mzero ≡ m

Filtering Again
class M[A] {
def map[B](f: A => B):M[B] = ...
def flatMap[B](f: A=> M[B]): M[B] = ...
def filter(p: A=> Boolean): M[A] = ...
}

Filter law
FIL1. m filter p ≡
m flatMap {x => if(p(x)) unit(x) else mzero}

Filter results 1
• m filter {x => true} ≡
m filter {x => true} // identity
m flatMap {x => if (true) unit(x) else mzero}
// by FIL1
m flatMap {x => unit(x)} // by definition of if
• FIL1a. m filter {x => true} ≡ m // by M1

Filter results 2
• m filter {x => false} ≡ m filter {x => false}
// identity
• m filter {x => false} ≡ m flatMap {x => if (false)
unit(x) else mzero} // by FIL1
• m filter {x => false} ≡ m flatMap {x => mzero}
// by definition of if
• FIL1b. m filter {x => false} ≡ mzero // by MZ1

Side Effects
m map g map f ≡ m map {x => (f(g(x)) }

Basis 3
Scala Haskell
FM1 m map f ≡ m flatMap {x => fmap f m ≡ m >>= x -> return (f x)
unit(f(x))}
M1 m flatMap unit ≡ m m >>= return ≡ m
M2 unit(x) flatMap f ≡ f(x) (return x) >>= f ≡ f x
M3 m flatMap g flatMap f ≡ m (m >>= f) >>= g ≡ m >>= (x -> f x >>= g)
flatMap {x => g(x) flatMap f}
MZ1 mzero flatMap f ≡ mzero mzero >>= f ≡ mzero
MZ2 m flatMap {x => mzero} ≡ mzero m >>= (x -> mzero) ≡ mzero
MZ3 mzero plus m ≡ m mzero 'mplus' m ≡ m
MZ4 m plus mzero ≡ m m 'mplus' mzero ≡ m
FIL1 m filter p ≡ m flatMap {x => mfilter p m ≡ m >>= (x -> if p x then
if(p(x)) unit(x) else mzero} return x else mzero)

Introduction to Monads in Scala (2)

More Related Content

What's hot

Viewers also liked

Similar to Introduction to Monads in Scala (2)

Recently uploaded

Introduction to Monads in Scala (2)