Introduction-to-Linear-Regression.pptx

Introduction-to-Linear-Regression.pptx

• 1.
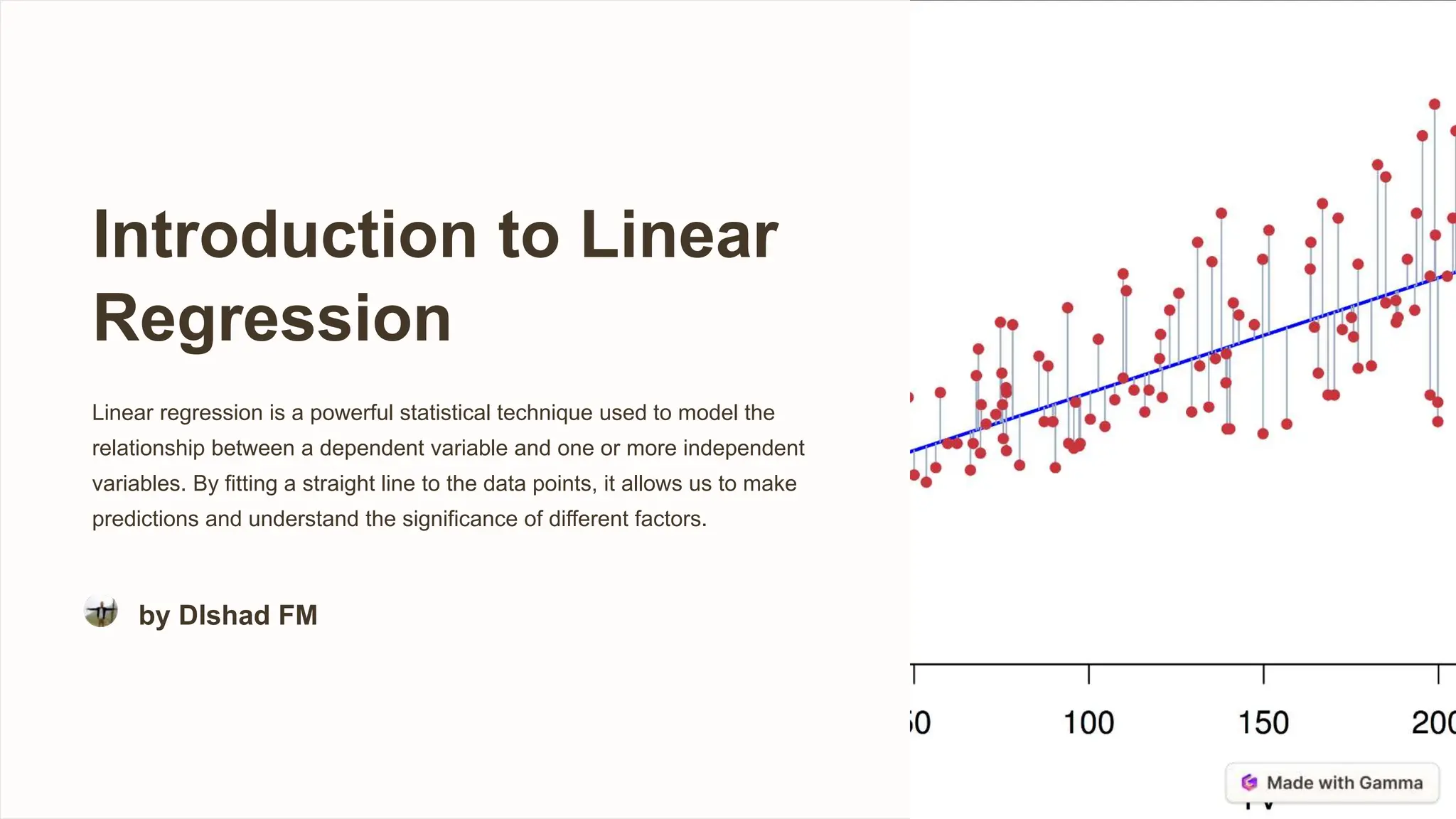
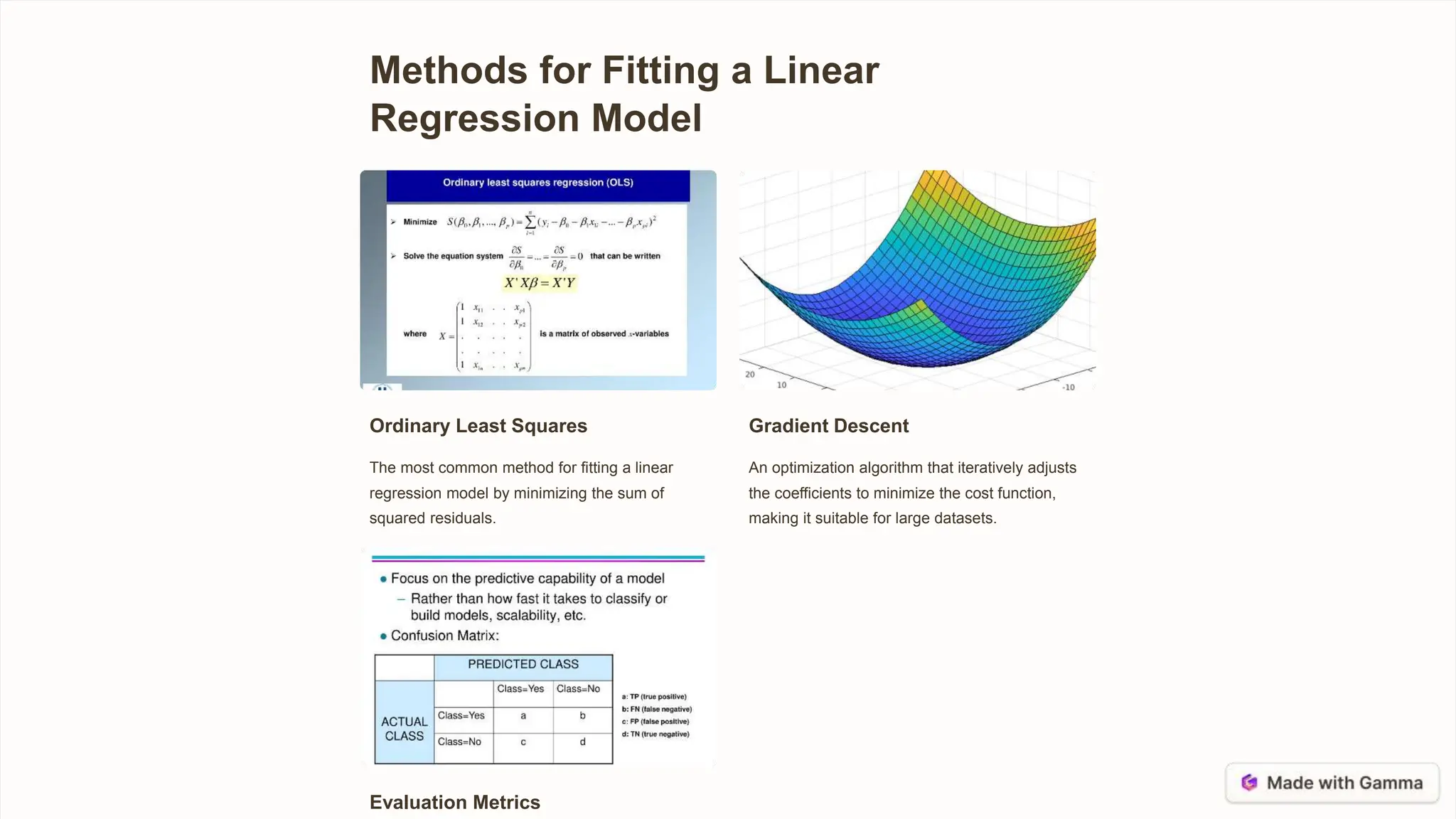
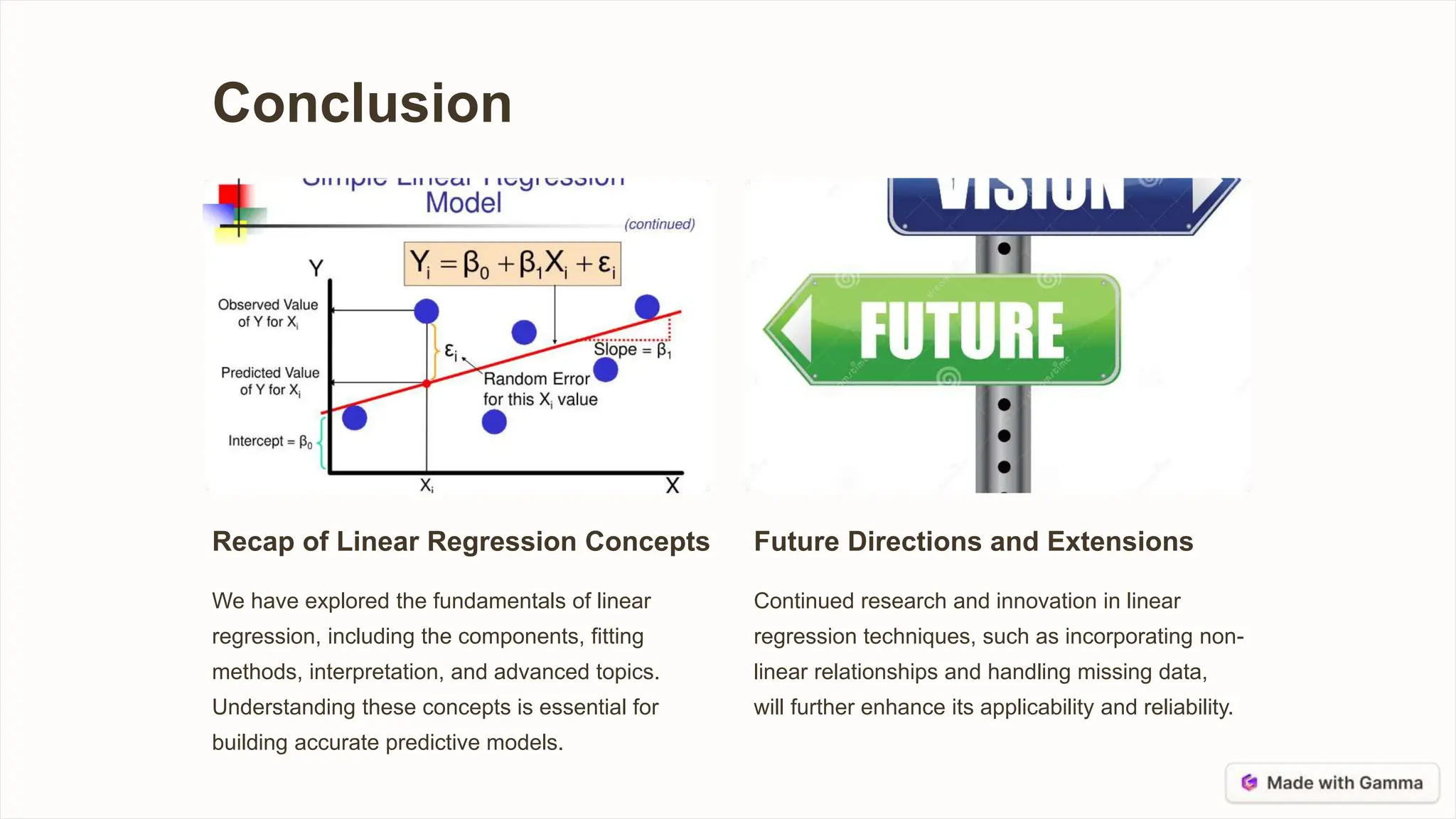
  Introduction to Linear Regression Linearregression is a powerful statistical technique used to model the relationship between a dependent variable and one or more independent variables. By fitting a straight line to the data points, it allows us to make predictions and understand the significance of different factors. by Dlshad FM
• 2.
  Understanding the Componentsof Linear Regression Dependent Variable The variable we are trying to predict or explain, also known as the outcome variable. Independent Variables The variables that we believe are related to the dependent variable and can help explain its variability. Coefficients and Intercept The coefficients represent the change in the dependent variable for a one-unit change in the corresponding independent variable. The intercept represents the value of the dependent variable when all independent variables are equal to zero. Assumptions and Limitations Linear regression relies on certain assumptions, such as linearity, independence, and normality of errors. It may not be appropriate for complex relationships or when assumptions are violated.
• 3.
  Methods for Fittinga Linear Regression Model Ordinary Least Squares The most common method for fitting a linear regression model by minimizing the sum of squared residuals. Gradient Descent An optimization algorithm that iteratively adjusts the coefficients to minimize the cost function, making it suitable for large datasets. Evaluation Metrics
• 4.
  Interpreting the Resultsof a Linear Regression Model 1 Assessing the Significance of Coefficients Hypothesis tests, such as the t-test, can determine whether the coefficients are significantly different from zero, indicating their importance in explaining the variation in the dependent variable. 2 Analyzing the Goodness of Fit R-squared, the coefficient of determination, measures the proportion of variance in the dependent variable that can be explained by the independent variables. A higher value indicates a better fit. 3 Interpreting the Prediction Accuracy By comparing the predicted values to the actual values, we can assess how well the model performs in making accurate predictions.
• 5.
  Advanced Topics inLinear Regression 1 Multicollinearity and Variable Selection When independent variables are highly correlated, multicollinearity can pose challenges in interpreting coefficients. Variable selection techniques, such as stepwise regression and Lasso, help identify critical predictors. 2 Polynomial Regression and Interaction Terms Including higher-order polynomial terms or interaction terms can capture non-linear relationships or interaction effects between variables. 3 Regularization Techniques Regularization methods, such as Ridge and Lasso regression, help prevent overfitting by adding a penalty to the coefficients, promoting simpler and more interpretable models.
• 6.
  Conclusion Recap of LinearRegression Concepts We have explored the fundamentals of linear regression, including the components, fitting methods, interpretation, and advanced topics. Understanding these concepts is essential for building accurate predictive models. Future Directions and Extensions Continued research and innovation in linear regression techniques, such as incorporating non- linear relationships and handling missing data, will further enhance its applicability and reliability.