Lec-35Graph - Graph - Copy in Data Structure

Shortest Path Problem in Graphs
1
Visit: tshahab.blogspot.com

Problem
 A motorist wishes to find the shortest possible route
from Islamabad to Lahore.
 Route map is given where distance between each pair
of adjacent intersections is marked.
 One possible way is to enumerate all the routes from
Islamabad to Lahore, add up the distance on each
route and select the shortest.
 There are hundreds and thousands of possibilities,
most of them are simply not worth considering.
2

Contd…
 A route from Islamabad to Peshawar to Lahore is
obviously a poor choice, as Peshawar is hundreds of
miles out of the way.
 In this presentation, we show how to solve such
problems efficiently.
3

Shortest path problem
 We are given a weighted, graph G=(V,E),
with weight function w:E->R mapping
edges to real-valued weights.
 The weight of path p=<v0,v1,…vk> is the
sum of the weights of its constituent
edges.
4

Variants
Assume that the graph is connected. The shortest
path problem has several different forms:
 Given two nodes A and B, find the shortest path
in the weighted graph from A to B.
 Given a node A, find the shortest path from A to
every other node in the graph. (single-source
shortest path problem)
 Find the shortest path between every pair of
nodes in the graph. (all-pair shortest path problem)
5

Single-Source Shortest Path
 Problem: given a weighted graph G, find
the minimum-weight path from a given
source vertex s to another vertex v
“Shortest-path” = minimum weight
Weight of path is sum of edges
6

Dijkstra’s Algorithm
 Similar to breadth-first search
Grow a tree gradually, advancing from vertices
taken from a queue
 Also similar to Prim’s algorithm for MST
Use a priority queue keyed on d[v]
7

The idea is to visit the nodes in order of their closeness to
A; visit A first, then visit the closest node to A, then the next
closest node to A, and so on.
The closest node to A, say X, must be adjacent to A and the
next closest node, say Y, must be either adjacent to A or X.
The third closest node to A must be either adjacent to A or X
or Y, and so on. (Otherwise, this node is closer to A than the
third closest node.)
8

The next node to be visited must be adjacent to some visited
node. We call the set of unvisited nodes that are adjacent to
an already visited node the fringe.
The algorithm then selects the node from the fringe closest to
A, say B, then visits B and updates the fringe to include the
nodes that are adjacent to B. This step is repeated until all the
nodes of the graph have been visited and the fringe is empty.
9

Dijkstra(G)
for each v  V
d[v] = ;
d[s] = 0; S = ; Q = V;
while (Q  )
u = ExtractMin(Q);
S = S U {u};
for each v  u->Adj[]
if (d[v] > d[u]+w(u,v))
d[v] = d[u]+w(u,v);
Relaxation
Step
Note: this
is really a
call to Q->DecreaseKey() 10

Dijkstra(G)
for each v  V
d[v] = ;
d[s] = 0; S = ; Q = V;
while (Q  )
u = ExtractMin(Q);
S = S U {u};
if (d[v] > d[u]+w(u,v))
d[v] = d[u]+w(u,v);
How many times is
ExtractMin() called?
How many times is
DecreaseKey() called?
What will be the total running time? 11

Dijkstra(G)
for each v  V
d[v] = ;
d[s] = 0; S = ; Q = V;
while (Q  )
u = ExtractMin(Q);
S = S U {u};
if (d[v] > d[u]+w(u,v))
d[v] = d[u]+w(u,v);
How many times is
ExtractMin() called?
How many times is
DecreaseKey() called?
A: O(E log V) using binary heap for Q 12

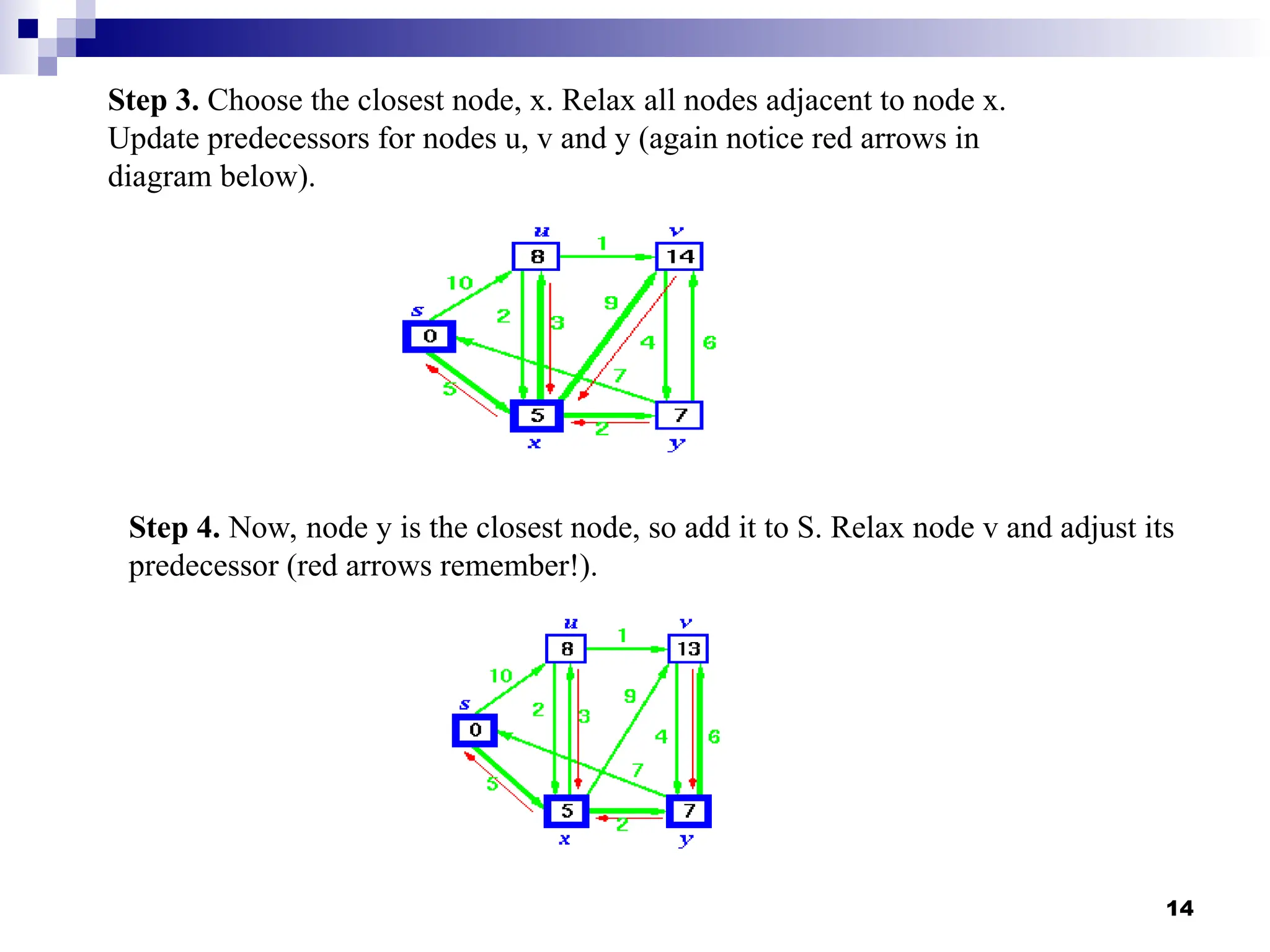
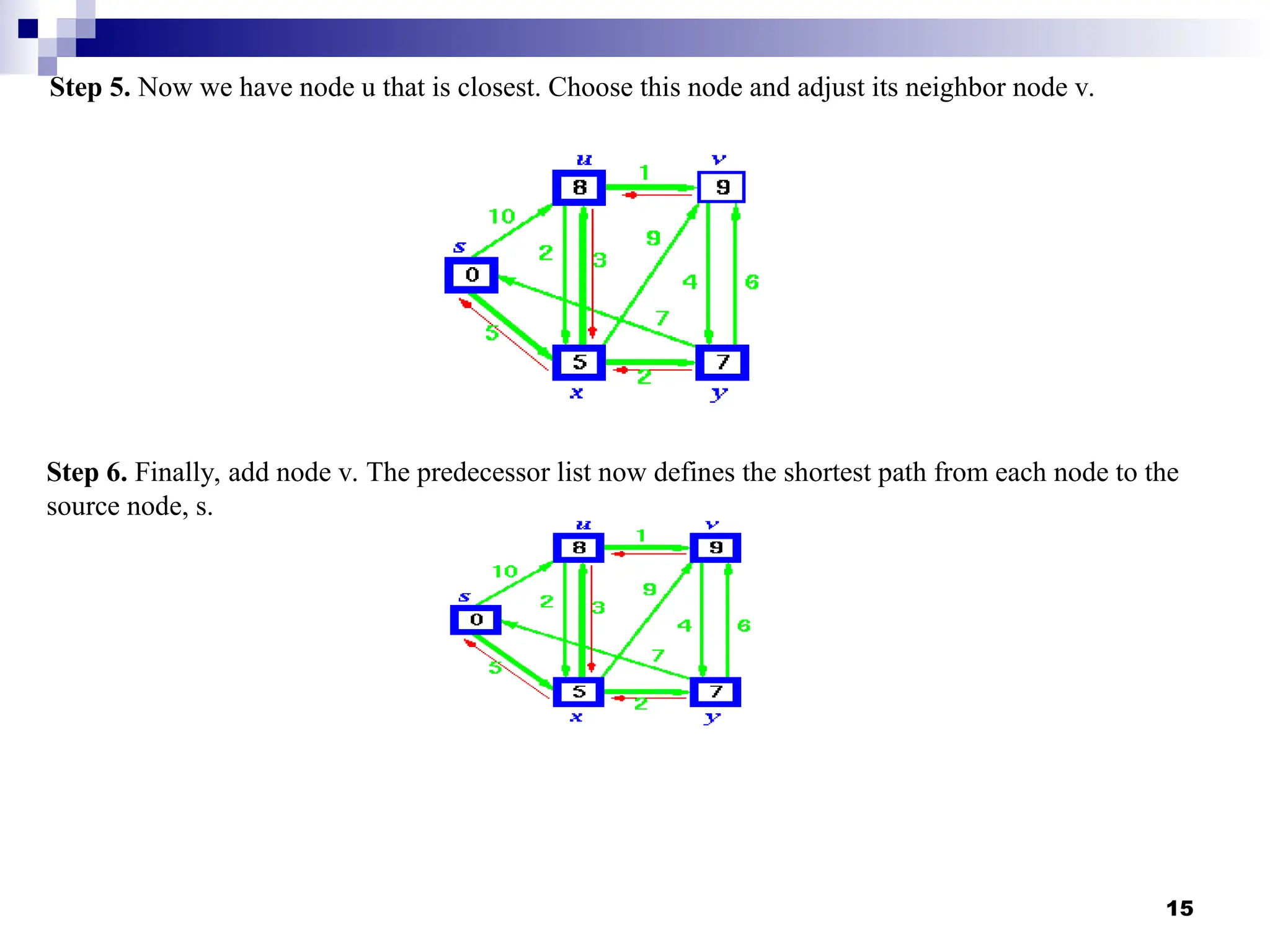
Step by Step operation of Dijkstra
algorithm
Step1. Given initial graph G=(V, E). All nodes have infinite cost
except the source node, s, which has 0 cost.
Step 2. First we choose the node, which is closest to the source node, s. We
initialize d[s] to 0. Add it to S. Relax all nodes adjacent to source, s. Update
predecessor (see red arrow in diagram below) for all nodes updated.
13

Step 3. Choose the closest node, x. Relax all nodes adjacent to node x.
Update predecessors for nodes u, v and y (again notice red arrows in
diagram below).
Step 4. Now, node y is the closest node, so add it to S. Relax node v and adjust its
predecessor (red arrows remember!).
14

Step 5. Now we have node u that is closest. Choose this node and adjust its neighbor node v.
Step 6. Finally, add node v. The predecessor list now defines the shortest path from each node to the
source node, s.
15

Analysis of Dijkstra Algorithm
Q as a linear array
EXTRACT_MIN takes O(V) time and there are |V| such operations.
Therefore, a total time for EXTRACT_MIN in while-loop is O(V2
). Since
the total number of edges in all the adjacency list is |E|. Therefore for-
loop iterates |E| times with each iteration taking O(1) time. Hence, the
running time of the algorithm with array implementation is O(V2
+ E) =
O(V2
).
Q as a binary heap ( If G is sparse)
In this case, EXTRACT_MIN operations takes O(log V) time and there
are |V| such operations. The binary heap can be build in O(V) time.
Operation DECREASE (in the RELAX) takes O(log V) time and there
are at most such operations.
Hence, the running time of the algorithm with binary heap provided
given graph is sparse is O((V + E) log V). Note that this time becomes
O(E logV) if all vertices in the graph is reachable from the source
vertices.
16

17
All Pairs Shortest Path Problem

18
All pairs shortest path
 The problem: find the shortest path between every
pair of vertices of a graph
 The graph: may contain negative edges but no
negative cycles
 A representation: a weight matrix where
W(i,j)=0 if i=j.
W(i,j)= if there is no edge between i and j.
W(i,j)=“weight of edge”

19
The weight matrix and the graph
1 2 3 4 5
1 0 1 1 5
2 9 0 3 2
3 0 4
4 2 0 3
5 3 0


  
 
  
v1 v2
v3
v4
v5
3
2
2
4
1
3
1
9
3
5

20
Solution
 Dijkstra’s Algorithm can be used.
How?
 Set each vertex as source and call Dijkstra’s
algo
 But we may solve the problem using direct
approach (Algorithm By Floyd)

21
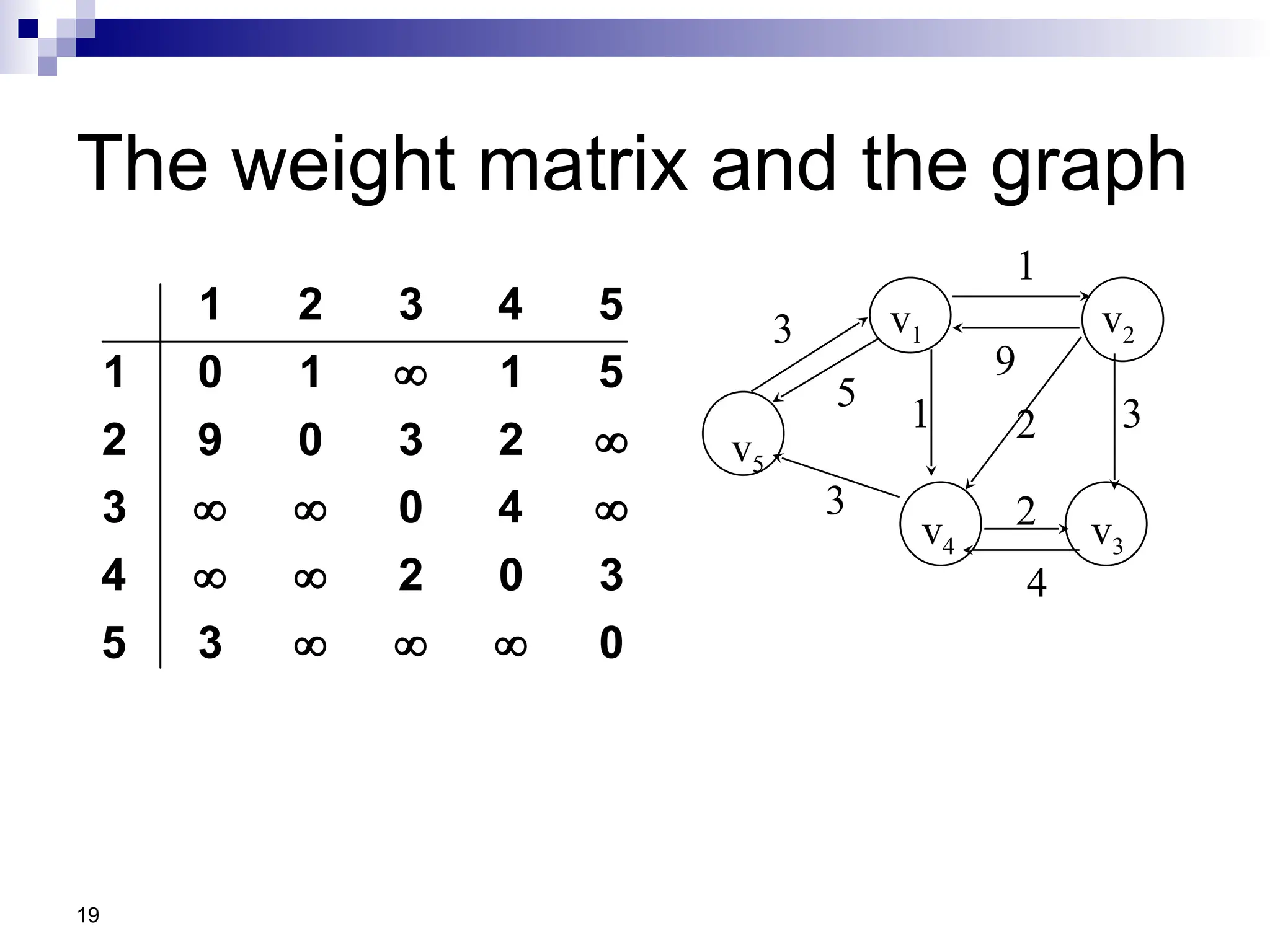
Floyd’s Algo
 Assume vertices are numbered as 1,2,3,…n for
simplicity
 Uses n×n matrix D (n is the number of vertices
in the graph G)
 Shortest paths are computed in matrix D
 After running the algorithm D[i,j] contains the
shortest distance (cost) between vertices i and j

22
Floyd’s Algo
 Initially we set D[i,j]=W[i,j]
 Remember
W[i,j]=0 if i==j
W(i,j)=∞ if there is no edge between i and j
W(i,j)=“weight of edge”
 We make n iteration over matrix D
 After kth iteration D[i,j] will store the value
of minimum weight path from vertex i to
vertex j that does not pass through a
vertex numbered higher than k

23
Floyd’s Algo
 In kth iteration we use following formula to compute D











]
,
[
]
,
[
]
,
[
min
]
,
[
1
1
1
j
k
D
k
i
D
j
i
D
j
i
D
k
k
k
k
● Subscript k denotes the value of matrix D after the kth
iteration (It should not be assumed there are n different
matrices of size n×n)

24
Vi
Vj
Vk
Shortest path using intermediate vertices
{V1, . . . Vk }

25
Floyed’s Algorithm
Floyd
1. D  W // initialize D array to W [ ]
2.
3. for k  1 to n
4. do for i  1 to n
5. do for j  1 to n
6. if (D[ i, j ] > D[ i, k ] + D[ k, j ] )
7. then D[ i, j ]  D[ i, k ] + D[ k, j ]

26
Recovering Paths
 Use another matrix P
 P[i,j] hold the vertex k that led Floyd to find
the smallest value of D[i,j]
 If P[i,j]=0 there is no intermediate edge
involved, shortest path is direct edge
between i and j
 So modified version of Floyd is given

27
Recovering Paths
Floyd
1. D  W // initialize D array to W [ ]
2. P  0
3. for k  1 to n
4. do for i  1 to n
5. do for j  1 to n
6. if (D[ i, j ] > D[ i, k ] + D[ k, j ] )
7. then D[ i, j ]  D[ i, k ] + D[ k, j ]
8. P [ i, j]  k

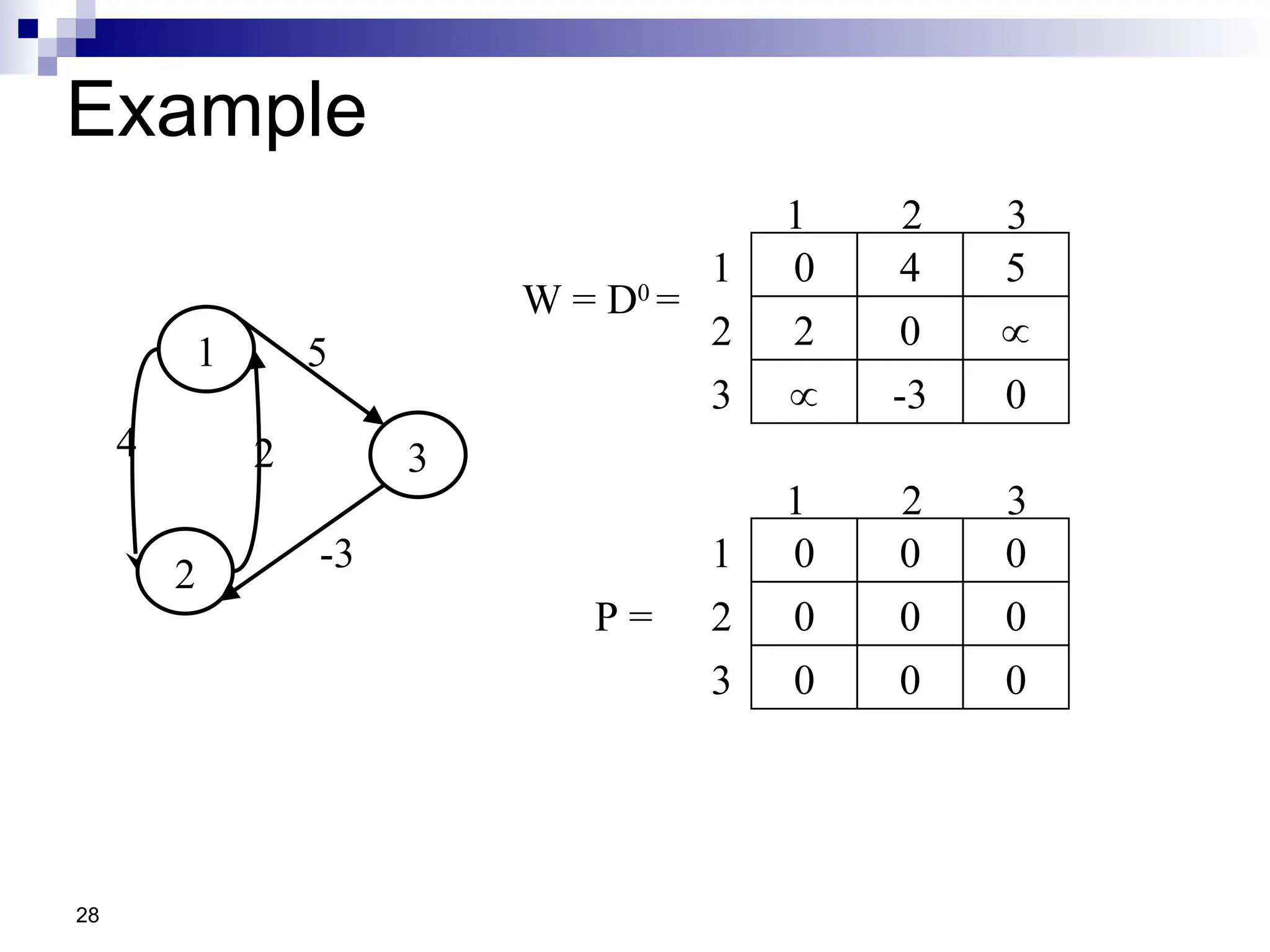
28
Example
W = D0
=
4
0 5
2 0 
 -3 0
1 2 3
1
2
3
0
0 0
0 0 0
0 0 0
1 2 3
1
2
3
P =
1
2
3
5
-3
2
4

29
D1
=
4
0 5
2 0 7
 -3 0
1 2 3
1
2
3
0
0 0
0 0 1
0 0 0
1 2 3
1
2
3
P =
1
2
3
5
-3
2
4
k = 1
Vertex 1 can be intermediate
node
D1
[2,3] = min( D0
[2,3], D0
[2,1]+D0
[1,3] )
= min (, 7)
= 7
D1
[3,2] = min( D0
[3,2], D0
[3,1]+D0
[1,2] )
= min (-3,)
= -3
4
0 5
2 0 
 -3 0
1 2 3
1
2
3
D0
=

30
D2
=
4
0 5
2 0 7
-1 -3 0
1 2 3
1
2
3
0
0 0
0 0 1
2 0 0
1 2 3
1
2
3
P =
D2
[1,3] = min( D1
[1,3], D1
[1,2]+D1
[2,3] )
= min (5, 4+7)
= 5
D2
[3,1] = min( D1
[3,1], D1
[3,2]+D1
[2,1] )
= min (, -3+2)
= -1
1
2
3
5
-3
2
4
D1
=
4
0 5
2 0 7
 -3 0
1 2 3
1
2
3
k = 2
Vertices 1, 2 can be
intermediate

31
D3
=
2
0 5
2 0 7
-1 -3 0
1 2 3
1
2
3
3
0 0
0 0 1
2 0 0
1 2 3
1
2
3
P =
D3
[1,2] = min(D2
[1,2], D2
[1,3]+D2
[3,2] )
= min (4, 5+(-3))
= 2
D3
[2,1] = min(D2
[2,1], D2
[2,3]+D2
[3,1] )
= min (2, 7+ (-1))
= 2
D2
=
4
0 5
2 0 7
-1 -3 0
1 2 3
1
2
3
1
2
3
5
-3
2
4 k = 3
Vertices 1, 2, 3 can be
intermediate

32
Printing intermediate nodes on
shortest path from i to j
Path (i, j)
k= P[ i, j ];
if (k== 0)
return;
Path (i , k);
print( k);
Path (k, j);
3
0 0
0 0 1
2 0 0
1 2 3
1
2
3
P =
1
2
3
5
-3
2
4

Lec-35Graph - Graph - Copy in Data Structure

More Related Content

Similar to Lec-35Graph - Graph - Copy in Data Structure

More from Anil Yadav

Recently uploaded

Lec-35Graph - Graph - Copy in Data Structure

Editor's Notes