Downloaded 46 times
Uploaded byAnshul Yadav
Lecture 6-cs648 Randomized Algorithms
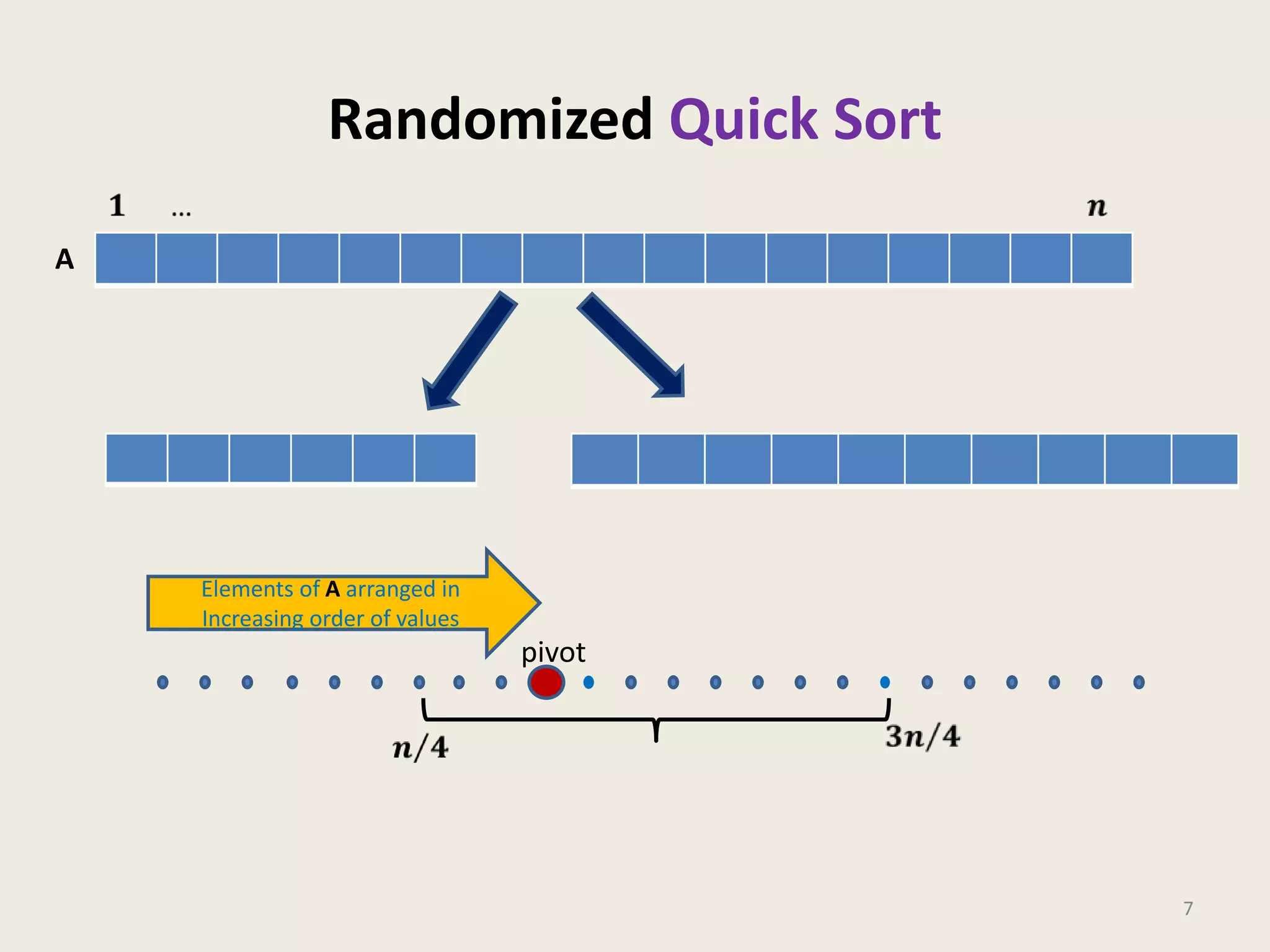
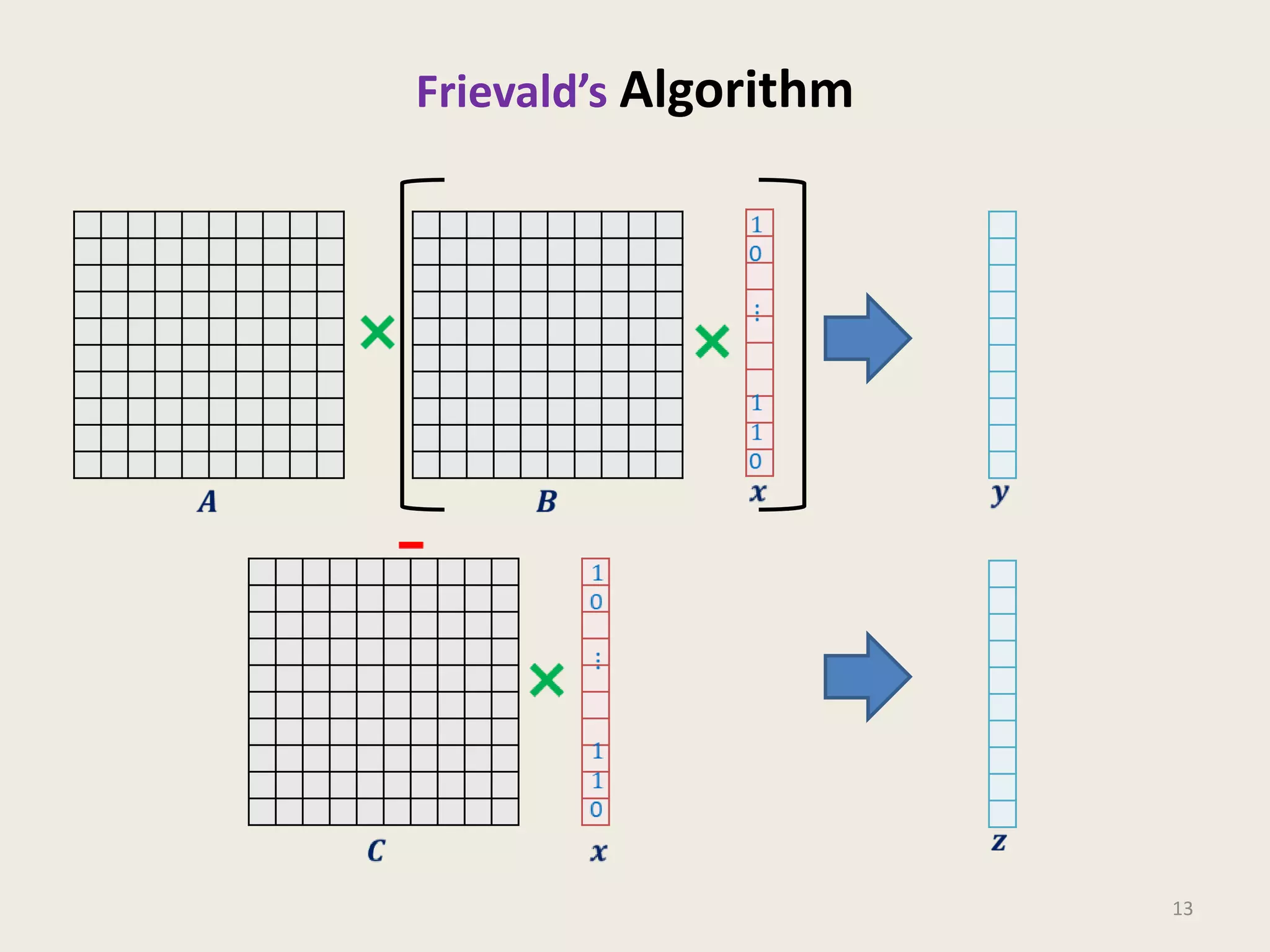
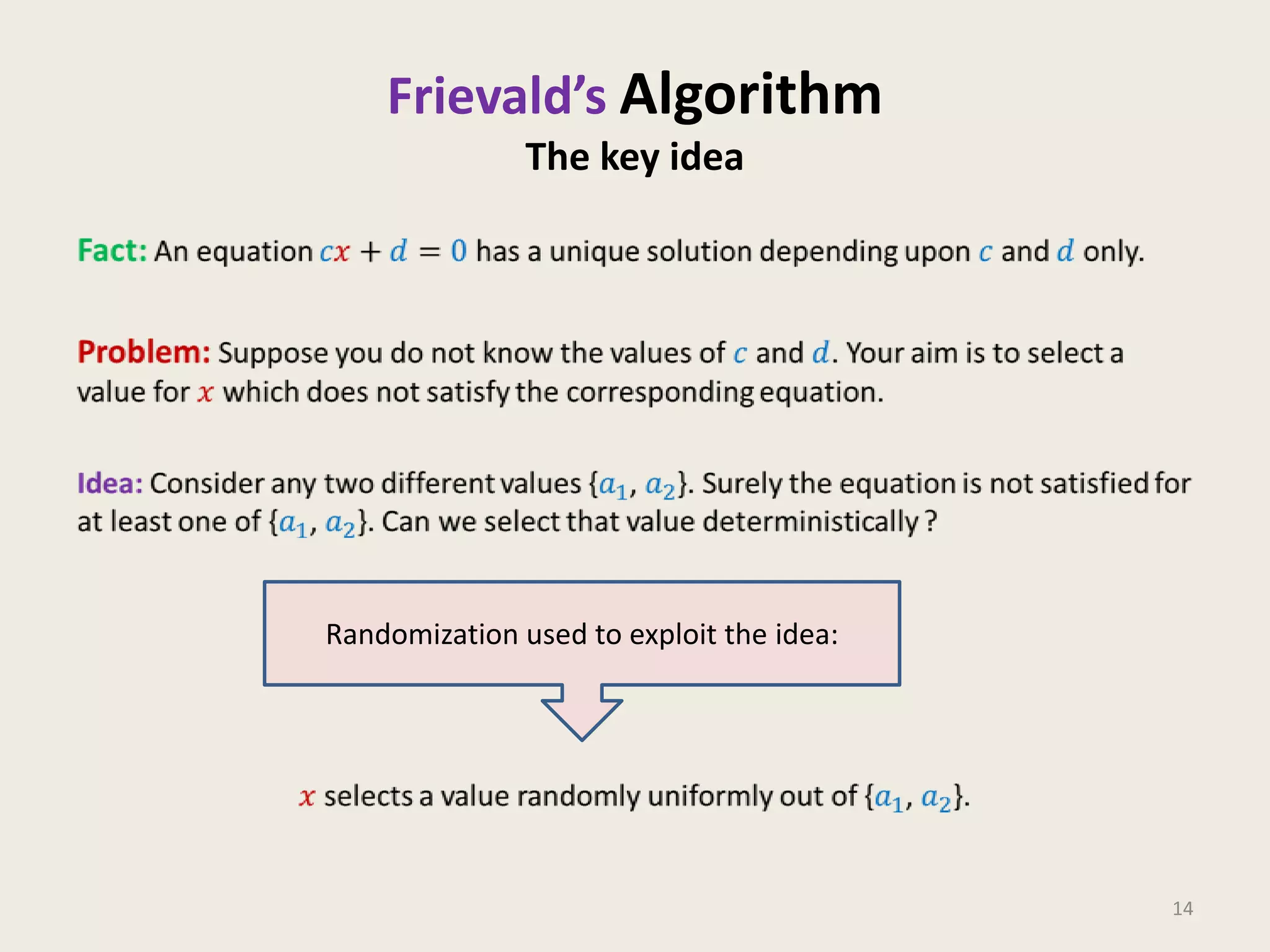
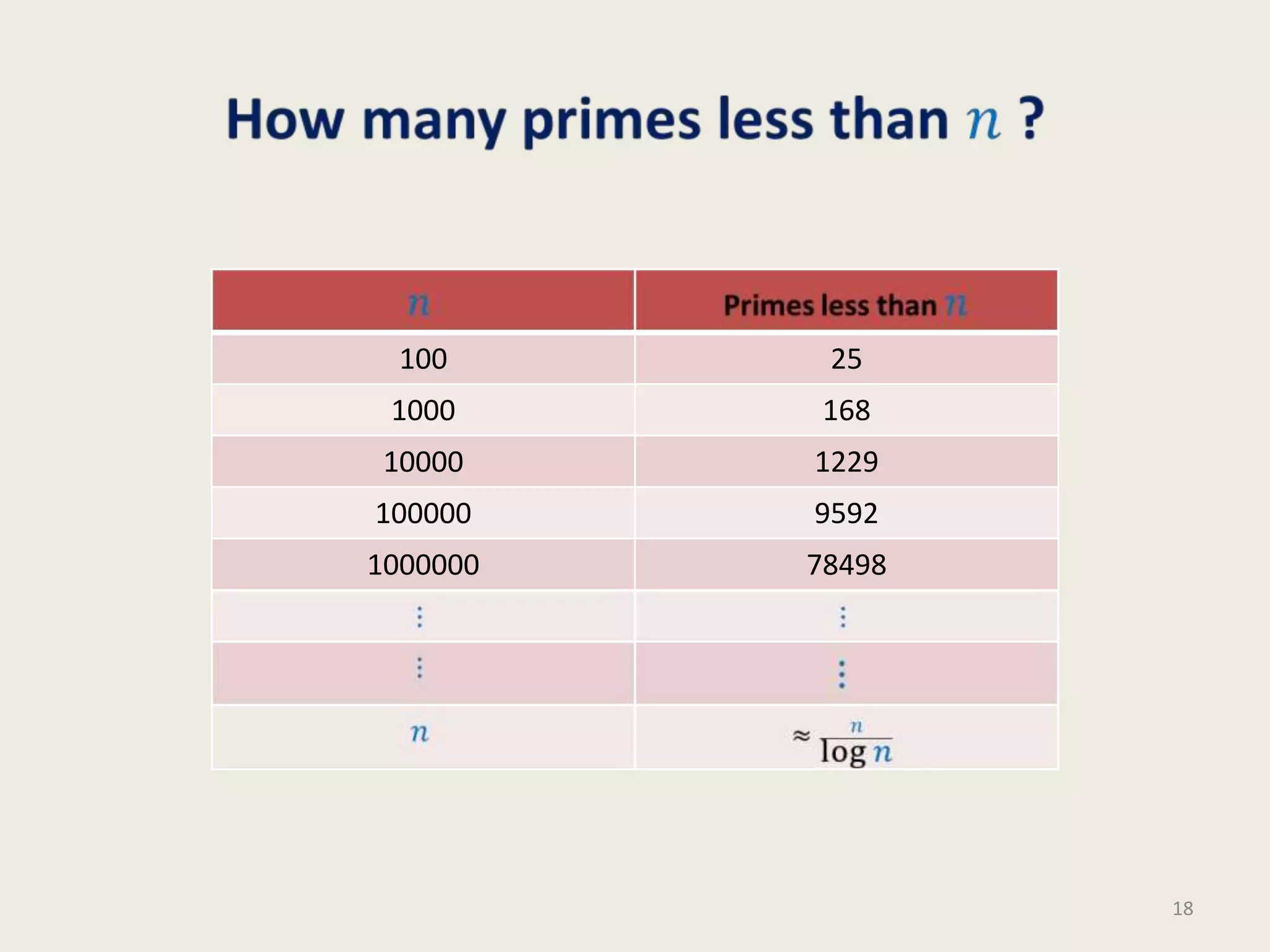
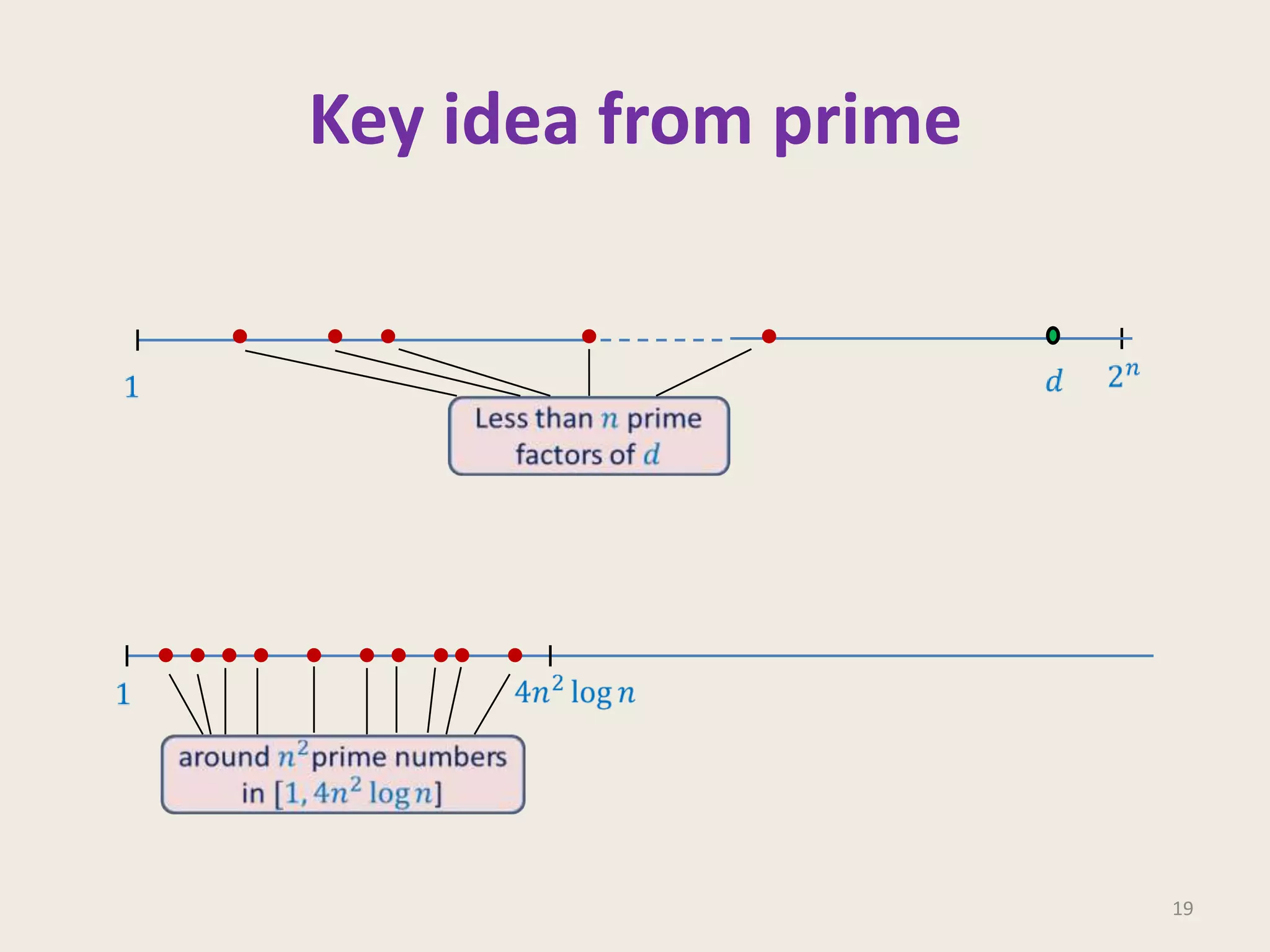
This document discusses randomized algorithms and provides examples. It reviews the last 3 lectures on randomized algorithms, including applications of fingerprinting techniques and 1-dimensional pattern matching. It then discusses randomized quicksort, the randomized algorithm for approximate median, Frievald's technique for matrix product verification, and randomized fingerprinting algorithms. It focuses on how randomization can be used to design algorithms and analyzes the error probabilities of randomized algorithms.
More Related Content
Similar to Lecture 6-cs648 Randomized Algorithms
Lecture 6-cs648 Randomized Algorithms
- 1. Randomized Algorithms CS648 Lecture 6 âąReviewing the last 3 lectures âą Application of Fingerprinting Techniques âą 1-dimensional Pattern matching âą Preparation for the next lecture. 1
- 2. Randomized Algorithms discussed tillnow âą Randomized algorithm for Approximate Median âą Randomized Quick Sort âą Frievaldâs algorithm for Matrix Product Verification âą Randomized algorithm for Equality of two files 2 Randomly select a sample Randomly permute the array Randomly select a vector Randomly select a prime number
- 3. Randomized Algorithms How doesone go about designing a randomized algorithm ? 3
- 4. Randomized Algorithms Some randomidea is required to design a randomized algorithm. 4
- 5. Randomized Algorithms An ideabased on insight into the problem Difficult/impossible to exploit the idea deterministically A randomized algorithm 5 Randomization to materialize the idea
- 6.
- 7. Randomized Quick Sort 7 Elementsof A arranged in Increasing order of values A pivot
- 8. Randomized Quick Sort Observation:There are many elements in A that are good pivot. Is it possible to select one good pivot efficiently ? (not possible deterministically ï) We select pivot element randomly uniformly. 8
- 9.
- 10. Randomized Algorithm for Approximatemedian A sample captures the essence of the original population. 10
- 11. Randomized Algorithm for Approximatemedian Idea: Is it possible to select a small subset of elements whose median approximates the median ? (not possible deterministically ï) Median of a uniformly random sample will be approximate median. 11 A random sample captures the essence of the original population.
- 12. FRIEVALDâS TECHNIQUE APPLICATION MATRIX PRODUCTVERIFICATION 12
- 13.
- 14. Frievaldâs Algorithm The keyidea 14 Randomization used to exploit the idea:
- 15. Frievaldâs Algorithm (Analyzing errorprobability) 15
- 16.
- 17. 17 Aim: To determineif File A identical to File B by communicating fewest bits ? File A File B
- 18. 18 100 25 1000 168 100001229 100000 9592 1000000 78498
- 19. Key idea fromprime 19
- 20. Visualize a fileas a binary number 20
- 21.
- 22.
- 23. Motivation ⹠Simplicity, realtime implementation, streaming environment ⹠Extension to 2-dimensions ⹠Converting Monte Carlo to Las Vegas algorithm 23 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 1 m⚯m n⚯n
- 24.
- 25.
- 26. 26 100101100110001101111010101010101010111010000101 0111101110110101 Small size but Notefficiently computable
- 27.
- 28. Fingerprint function: howgood is it ? 28 100101100110001101111010101010101010111010000101 0111101110110101
- 29. Bounding the errorprobability of the algorithm 29
- 30.
- 31. Probability tool (uniontheorem) 31
- 32. APPLICATIONS OF THE UNIONTHEOREM 32
- 33. Balls into Bins 33 12 3 ⊠i ⊠n 1 2 3 4 5 ⊠m-1 m
- 34. Balls into Bins 34 12 3 ⊠i ⊠n 1 2 3 4 5 ⊠m-1 m
- 35.