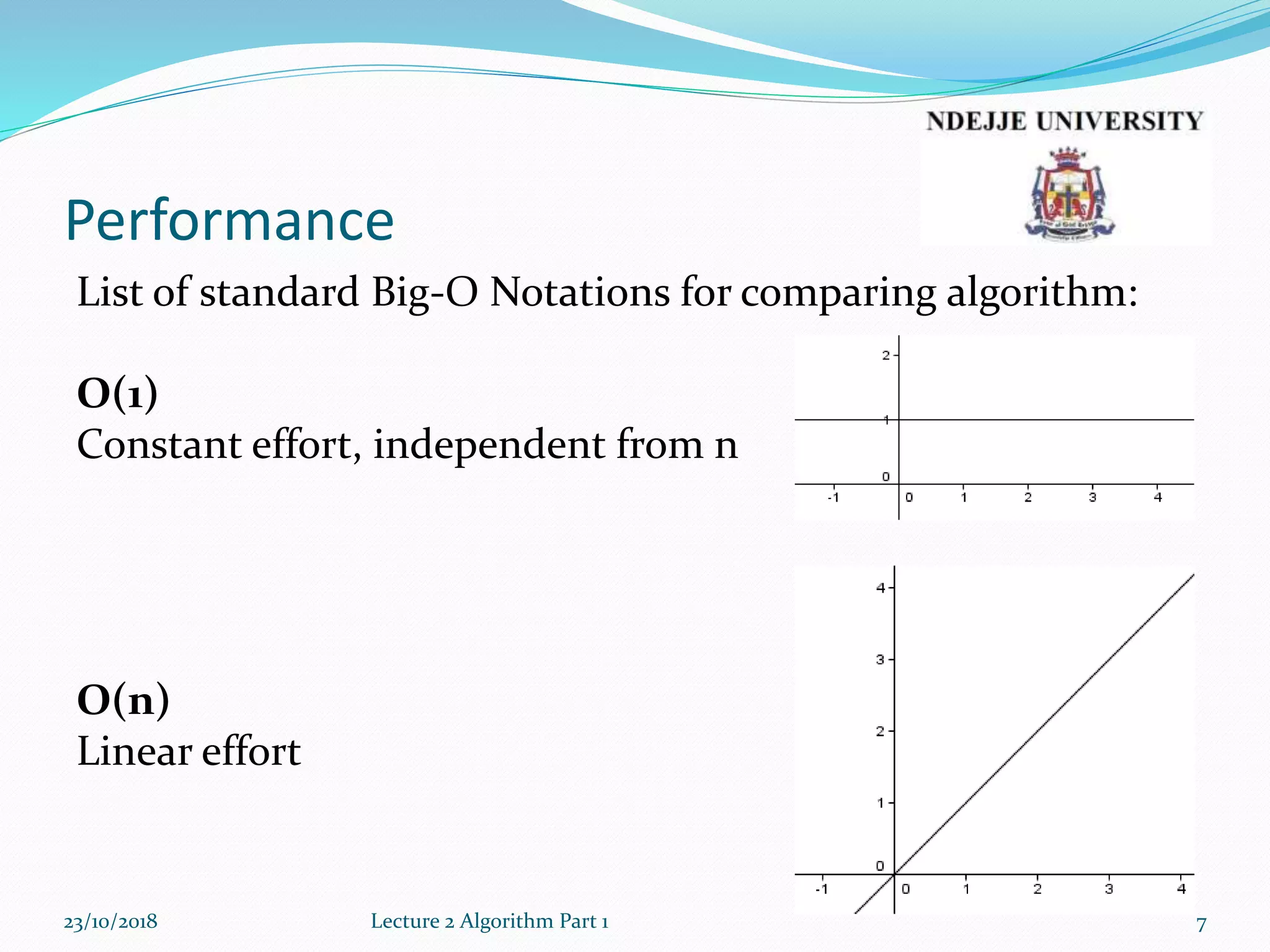
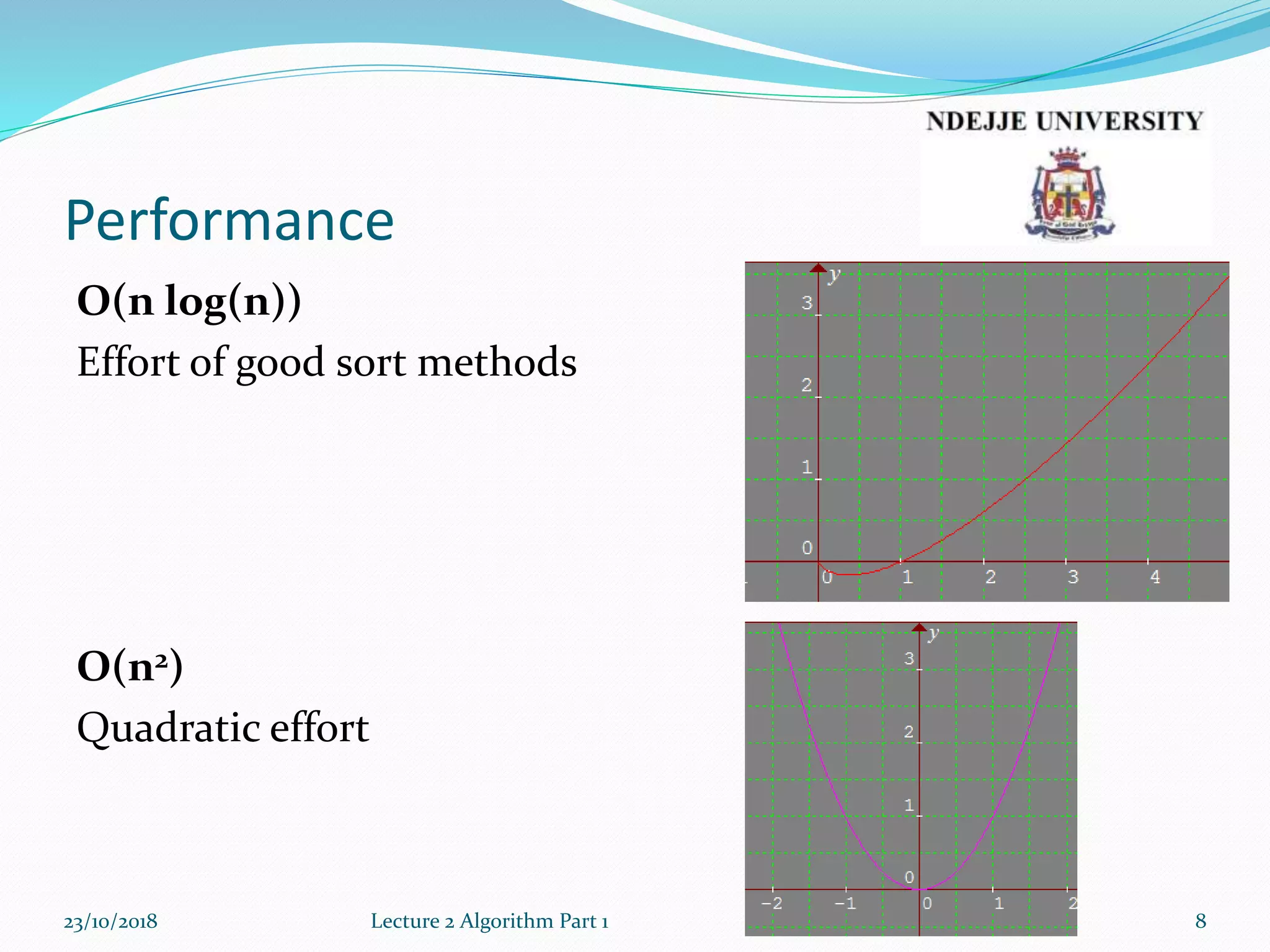
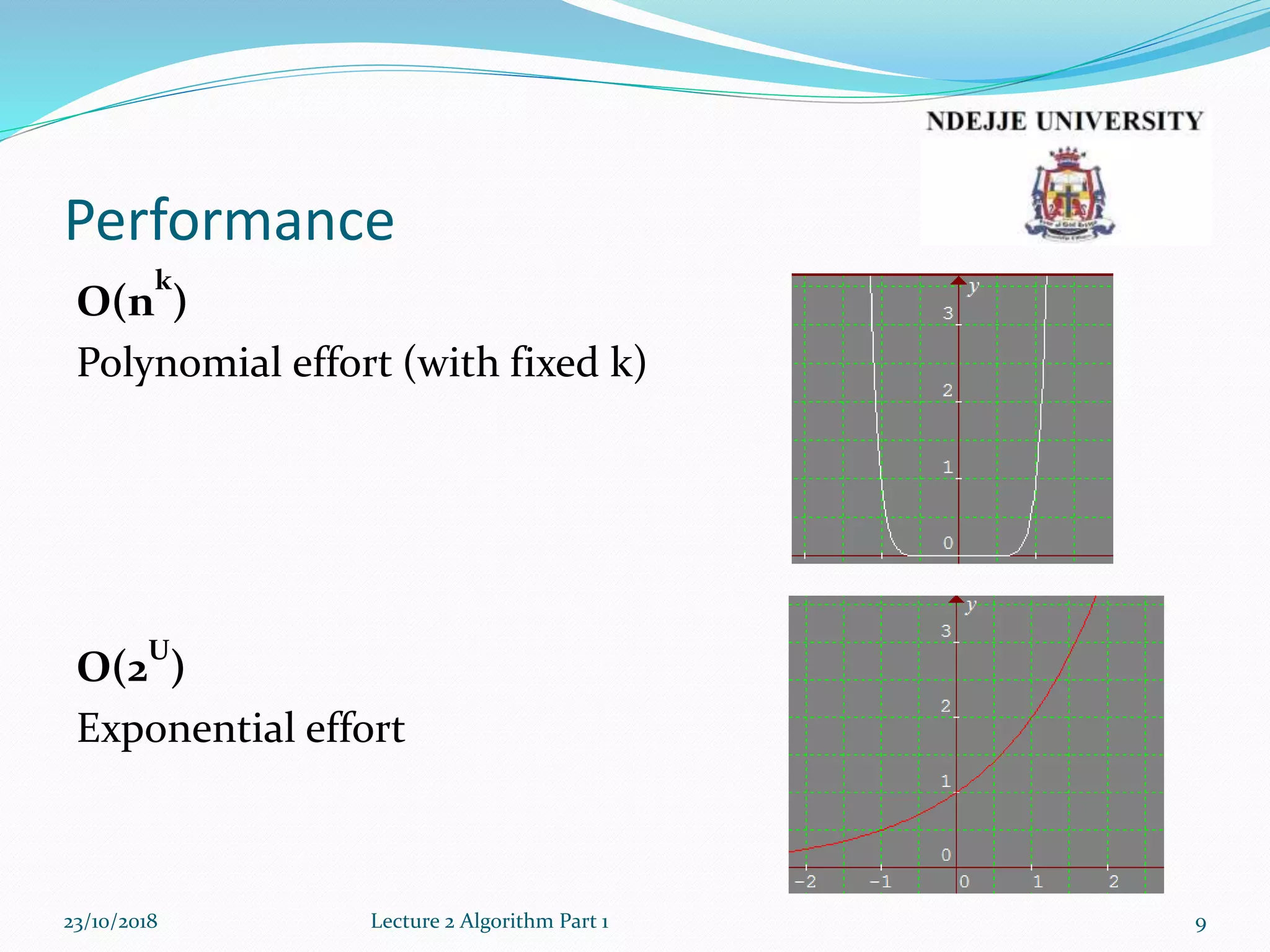
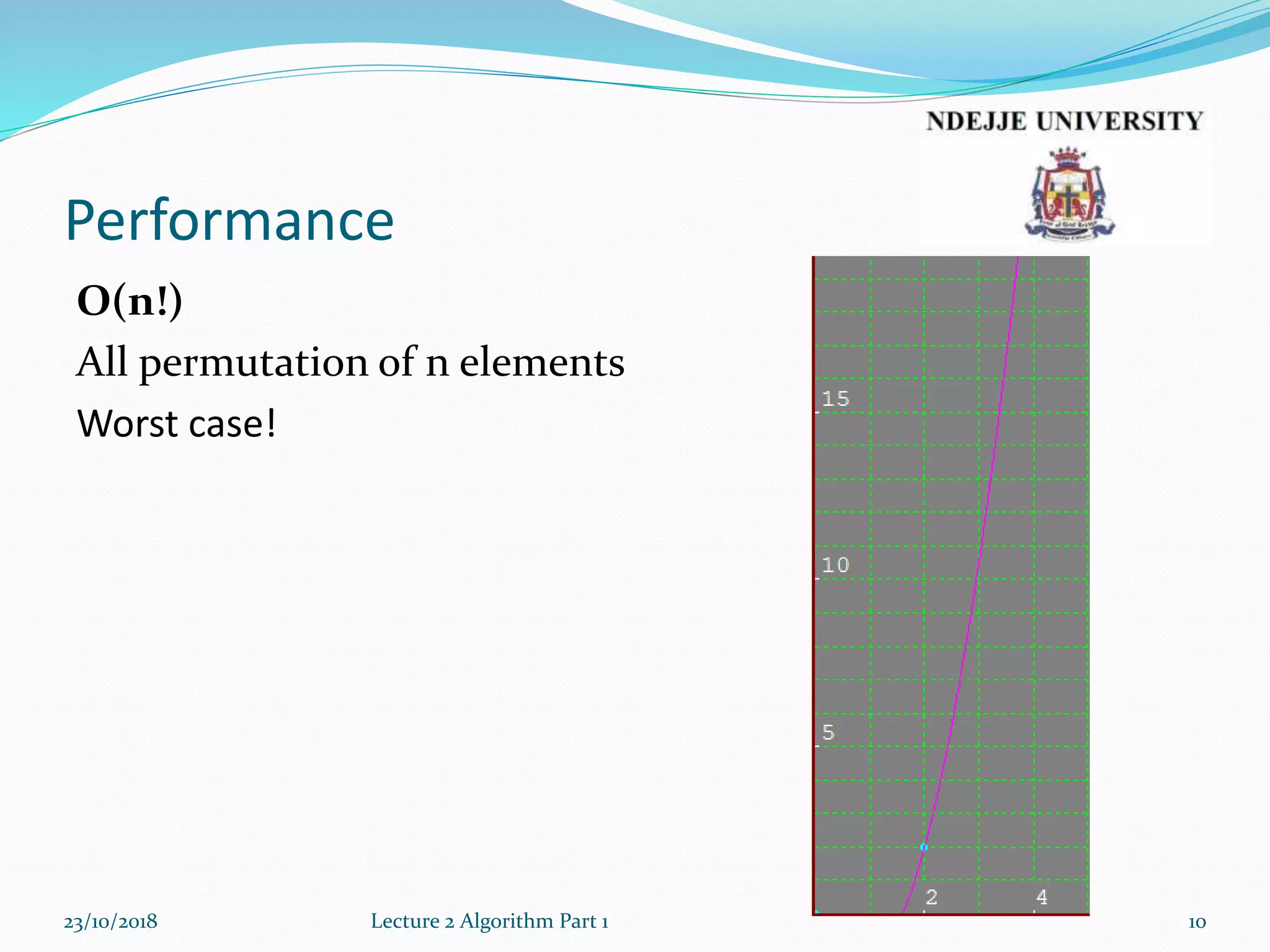
This document provides an overview of algorithms and recursion from a lecture. It discusses performance analysis using Big O notation. Common time complexities like O(1), O(n), O(n^2) are introduced. The document defines an algorithm as a set of well-defined steps to solve a problem and categorizes algorithms as recursive vs iterative, logical, serial/parallel/distributed, deterministic/non-deterministic, exact/approximate, and quantum. Examples of recursive algorithms like factorials, greatest common divisor, and the Fibonacci sequence are presented along with their recursive definitions and code implementations.



































![Peano-Hilbert curve
The Peano-Hilbert curves were discovered by Peano and
Hilbert in 1890/1891
They convert against a function which maps the interval
[0,1] of the real numbers surjective on the area [0,1] x [0,1]
and is in the same time constant
That means through repeatedly execute the function rules
you will reach every point in a square
23/10/2018 Lecture 2 Algorithm Part 1 40](https://image.slidesharecdn.com/lecture2aalgorithm-181023121505/75/Lecture2a-algorithm-40-2048.jpg)





