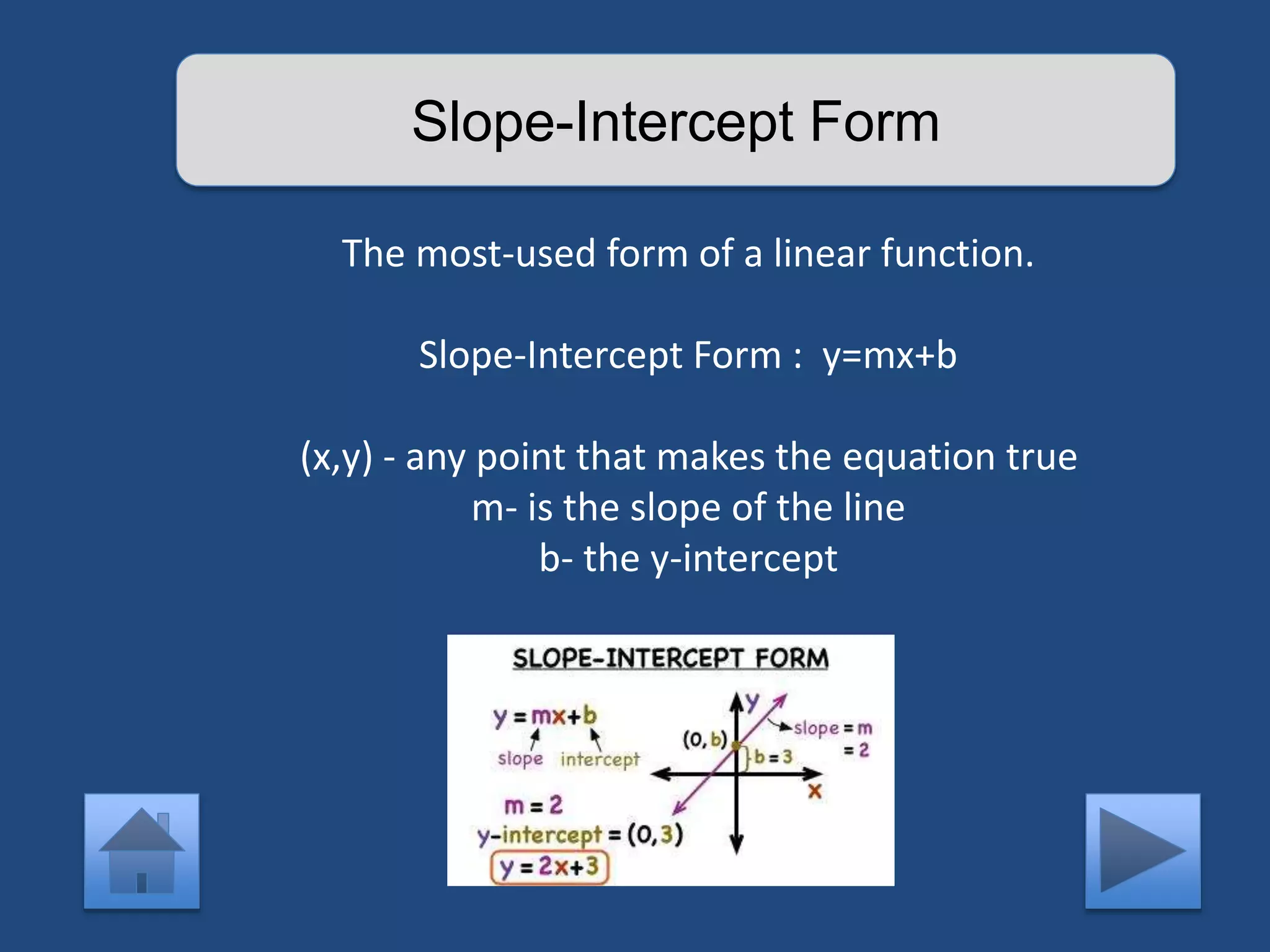
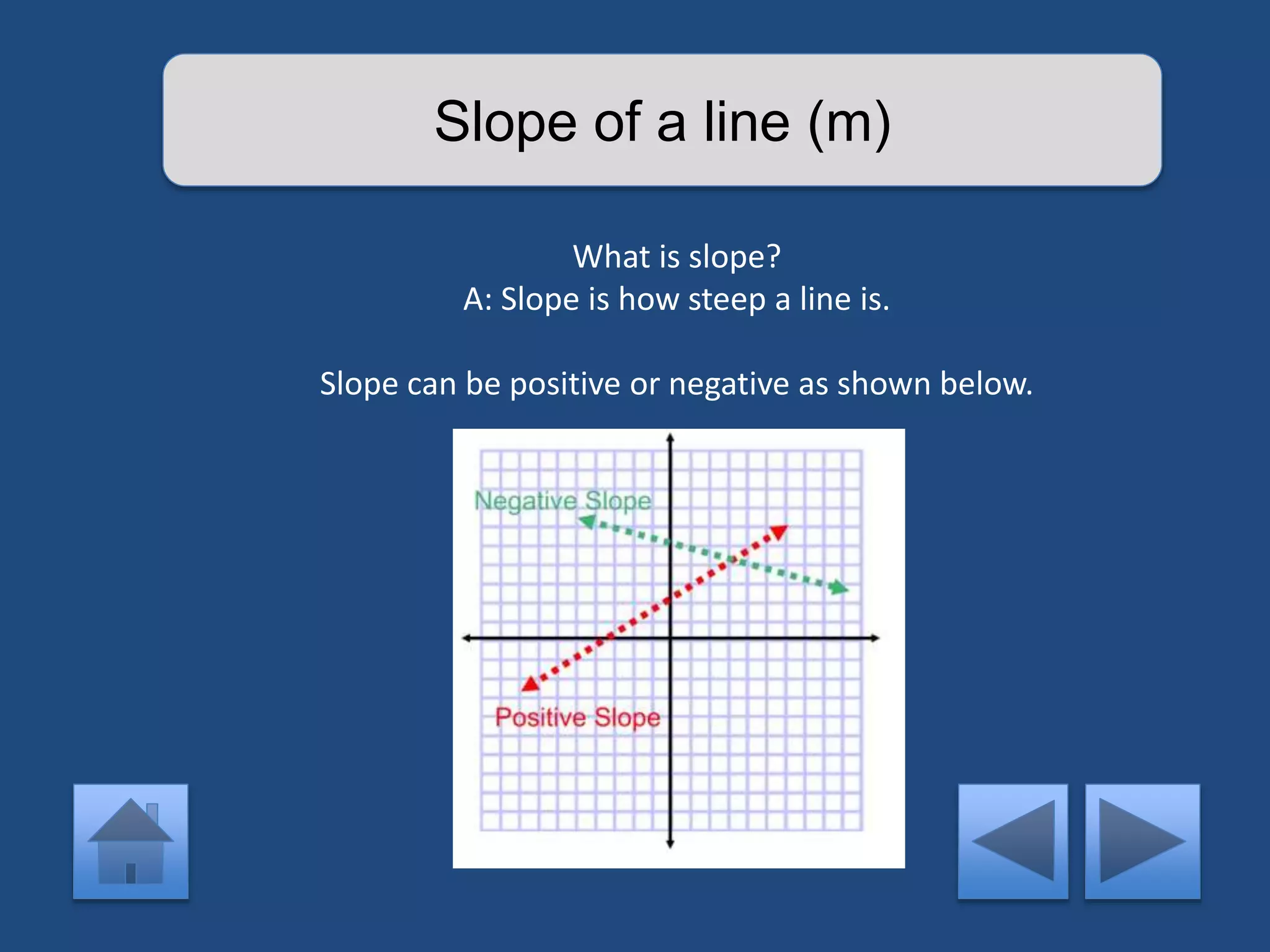
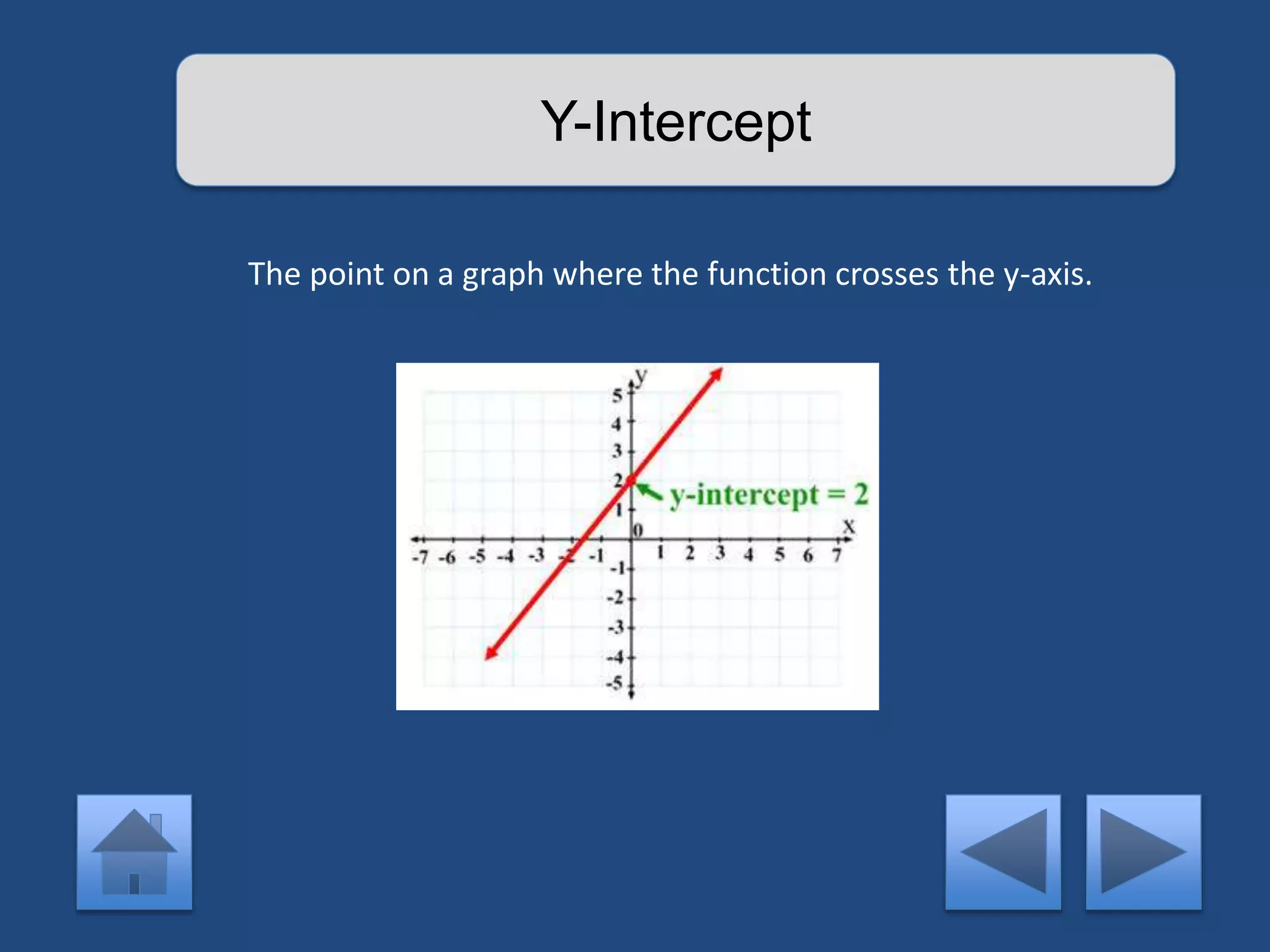
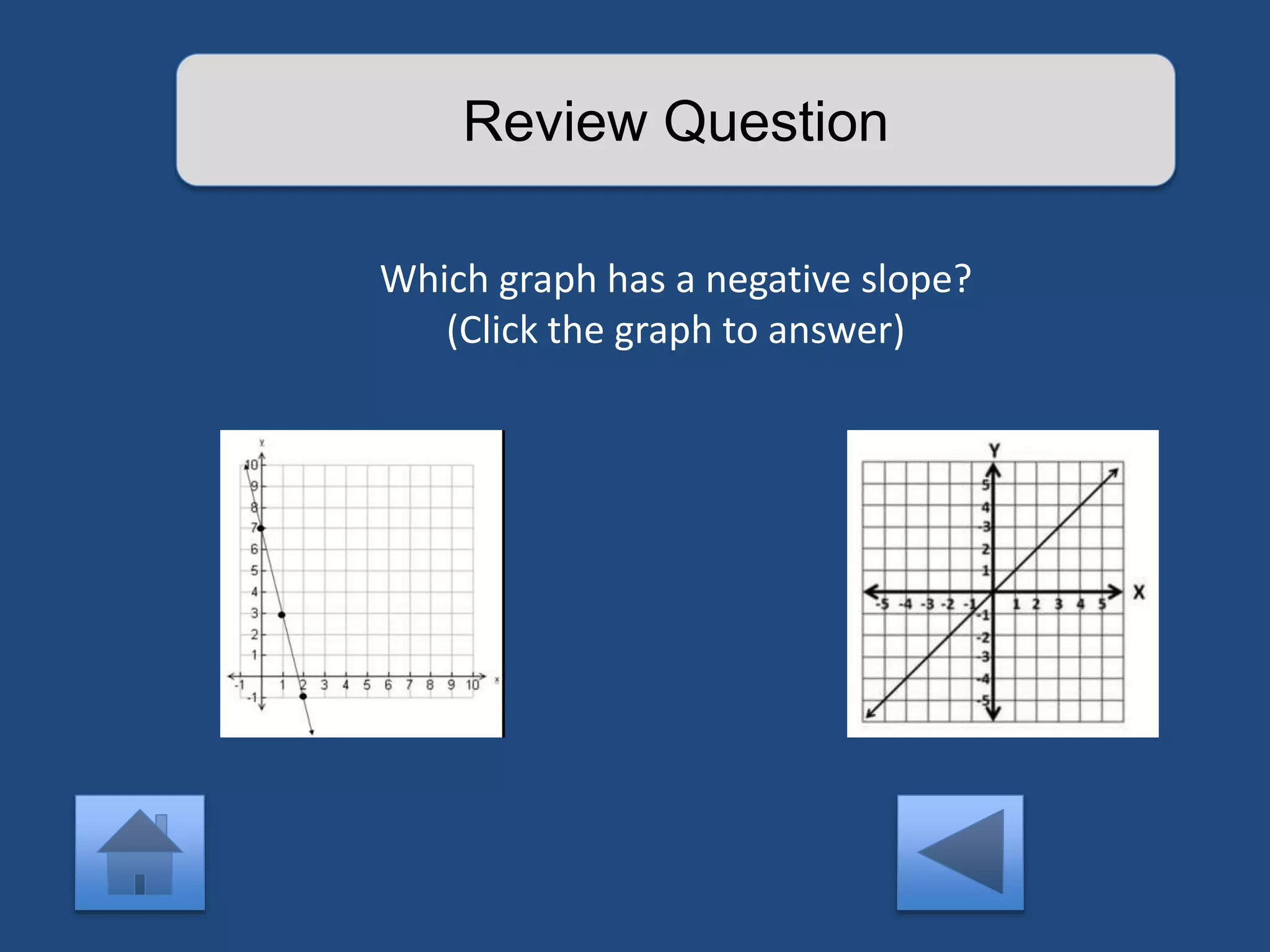
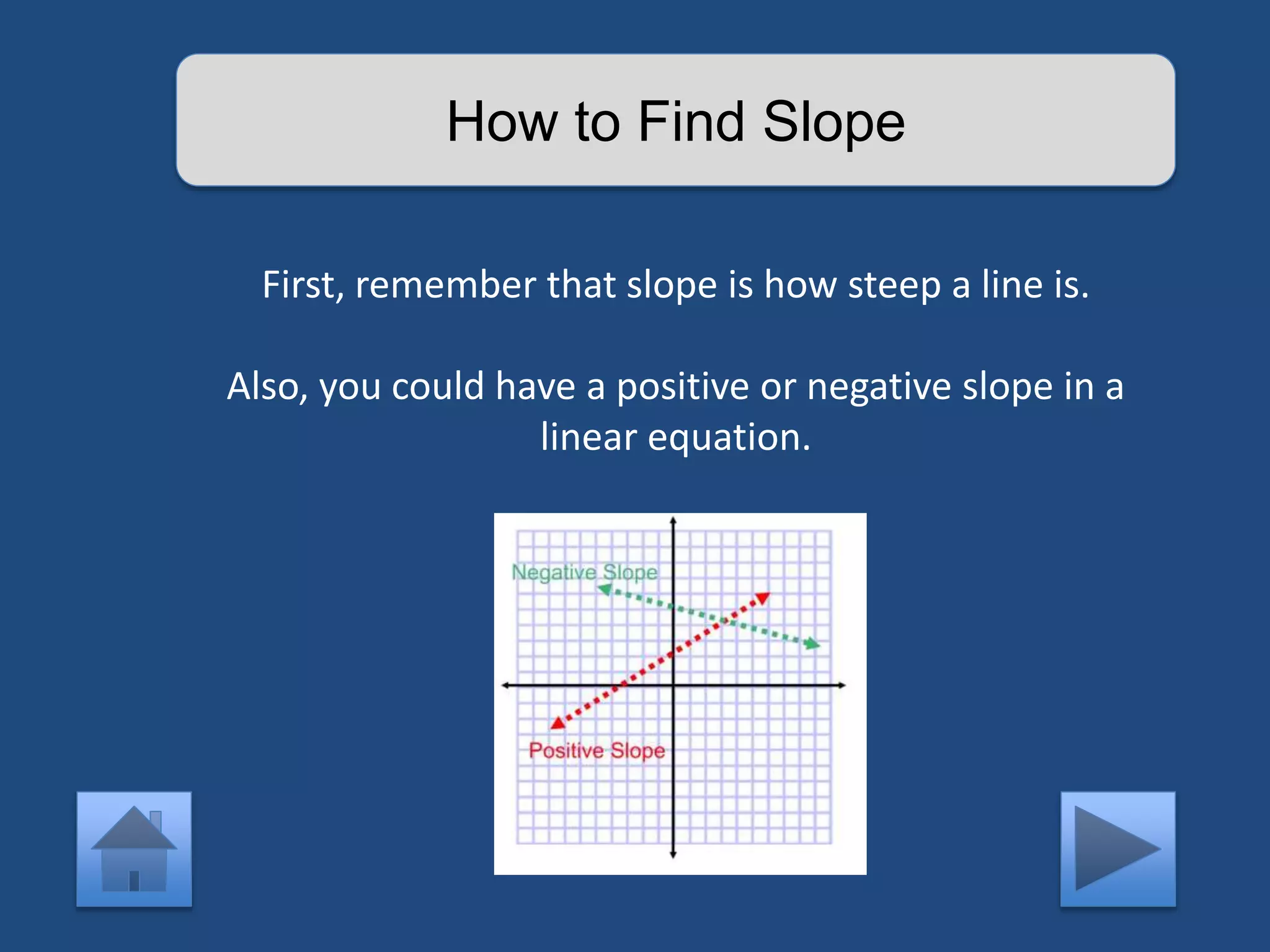
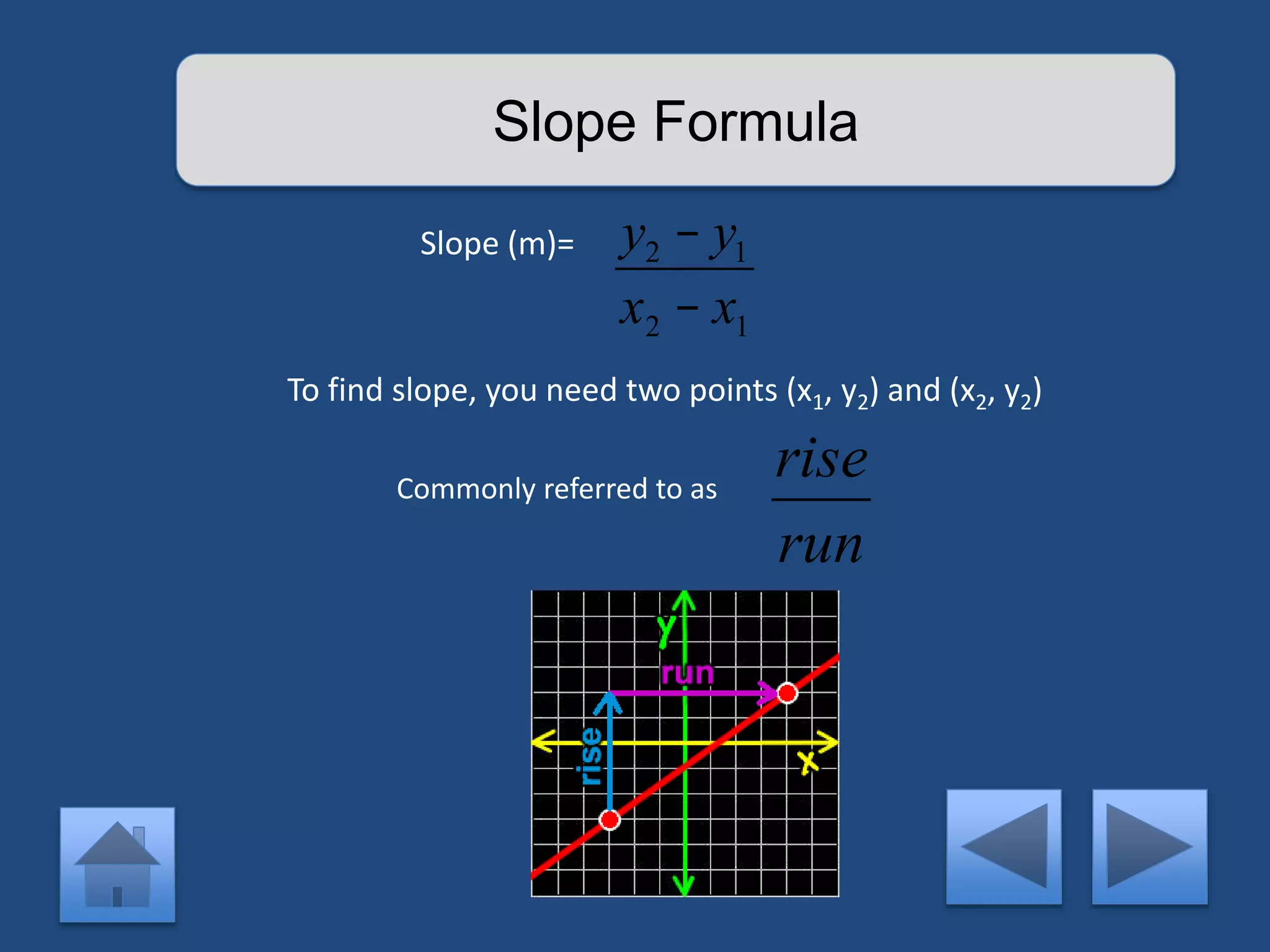
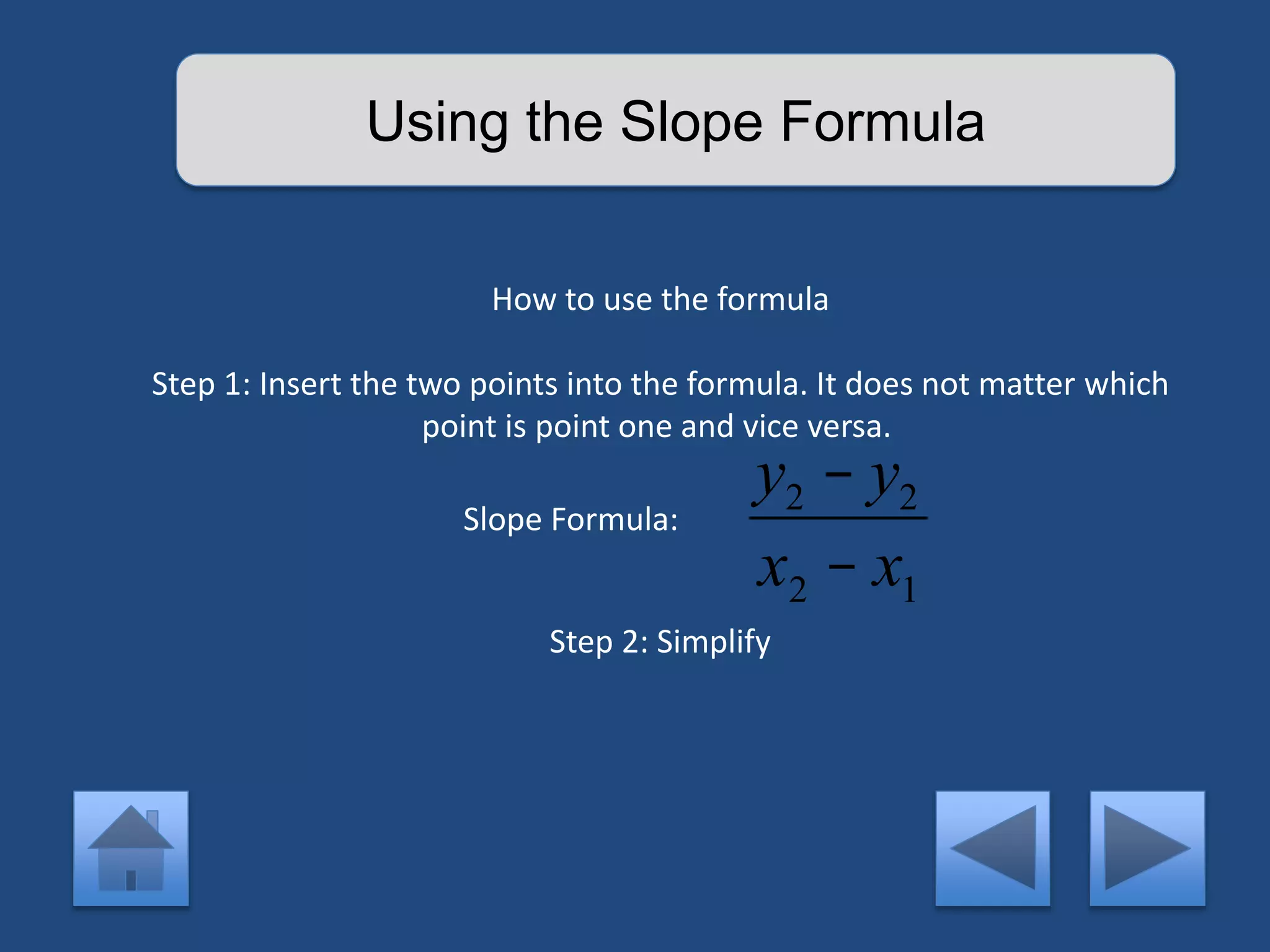
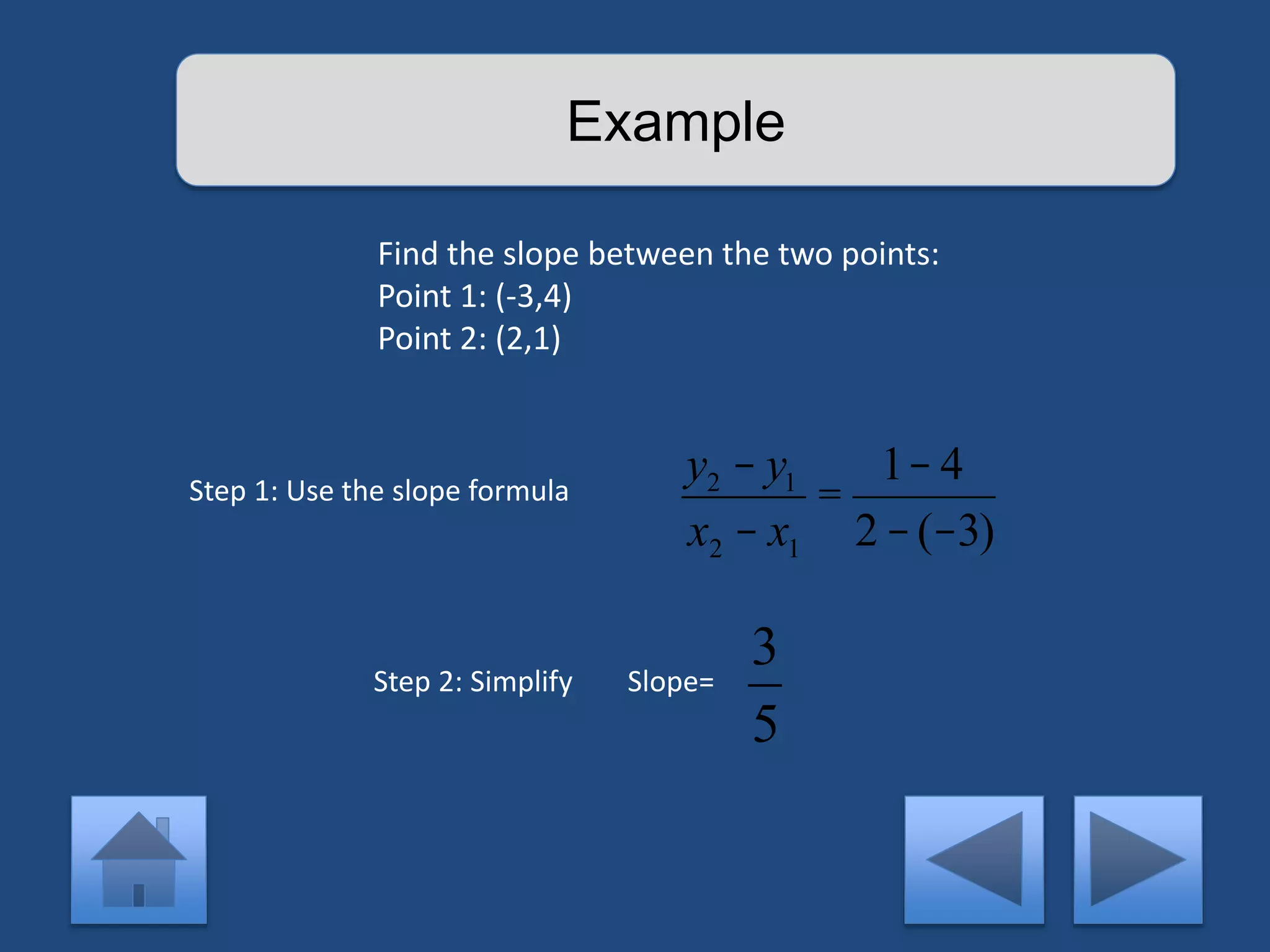
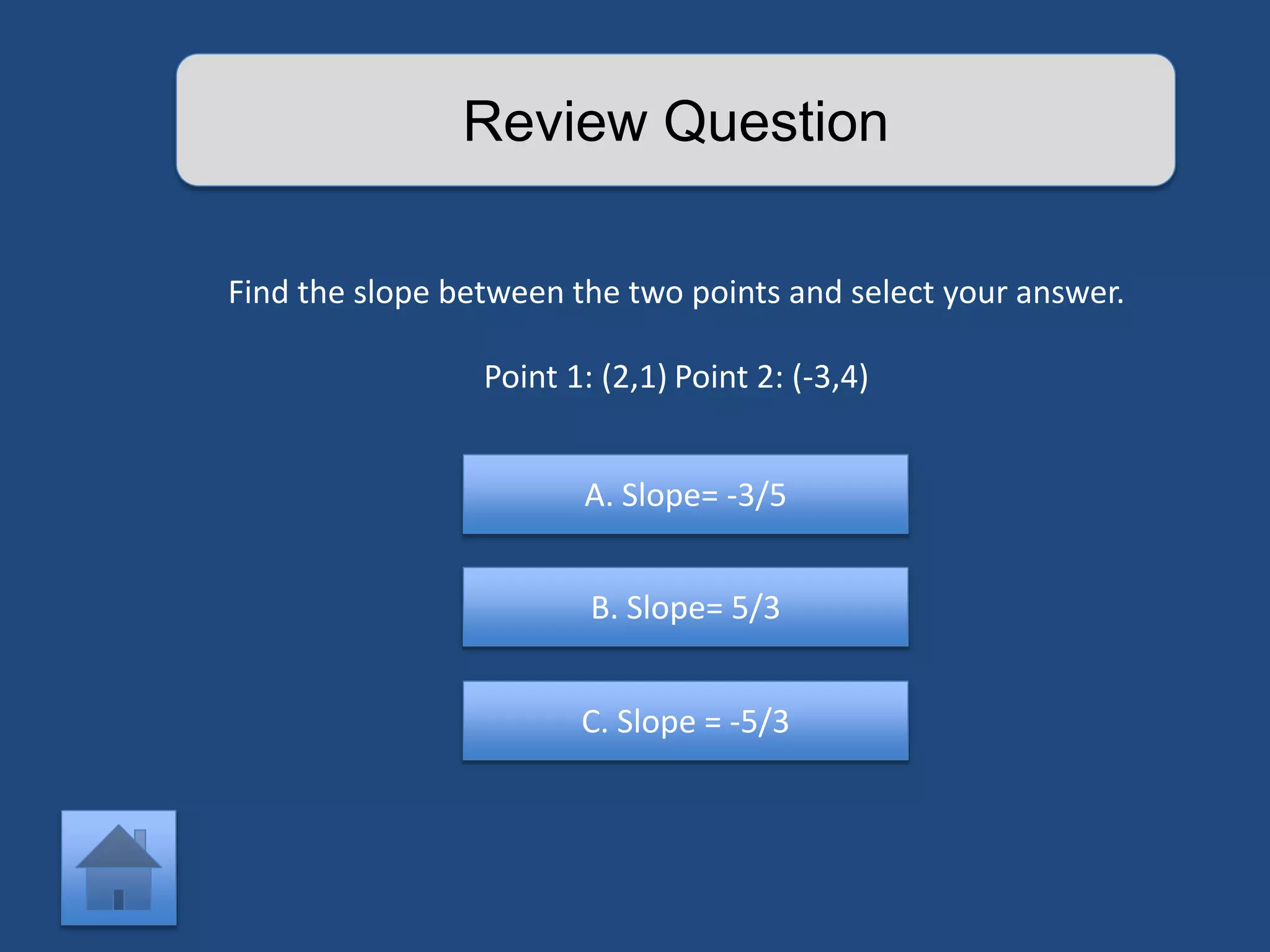
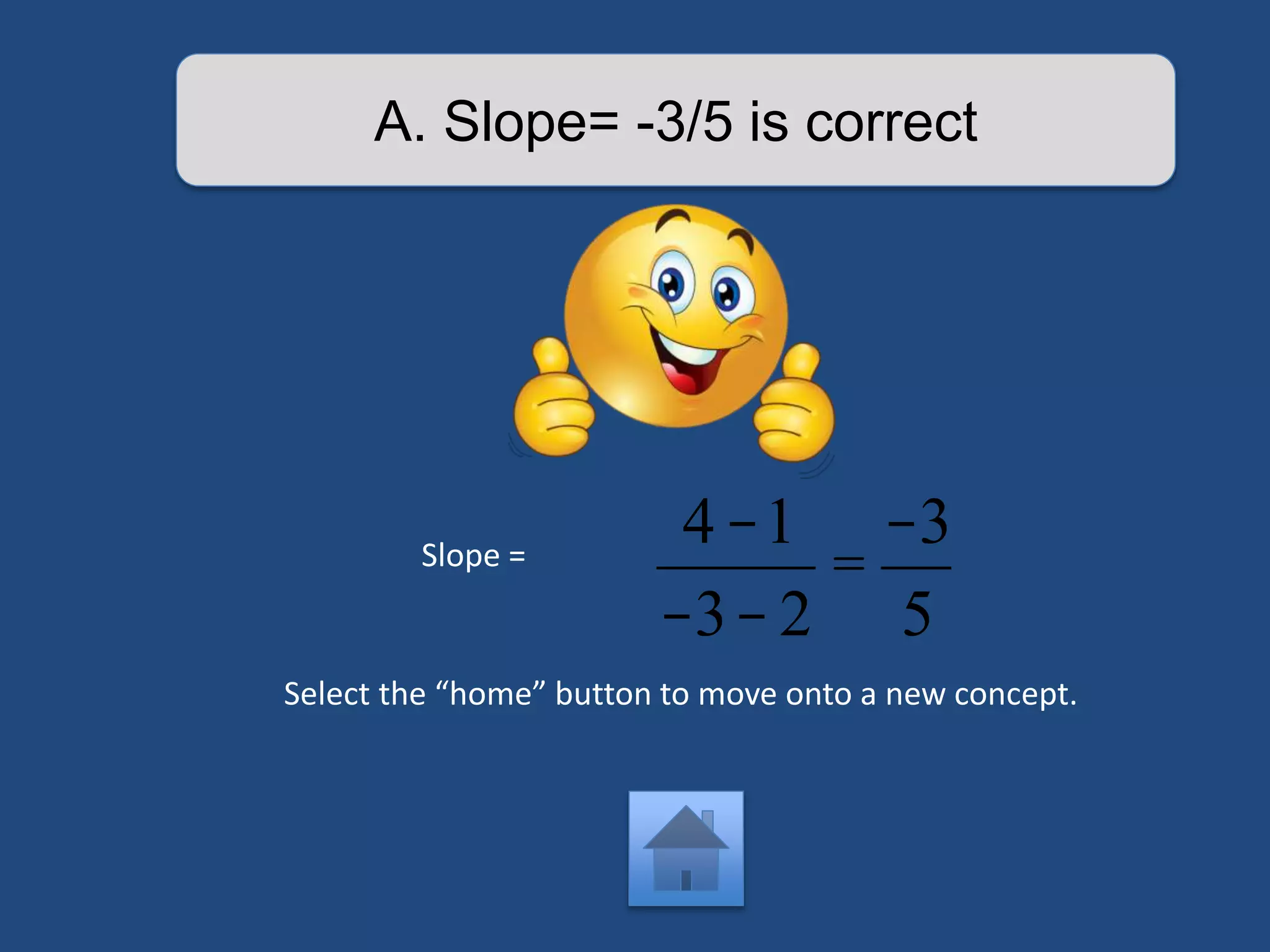
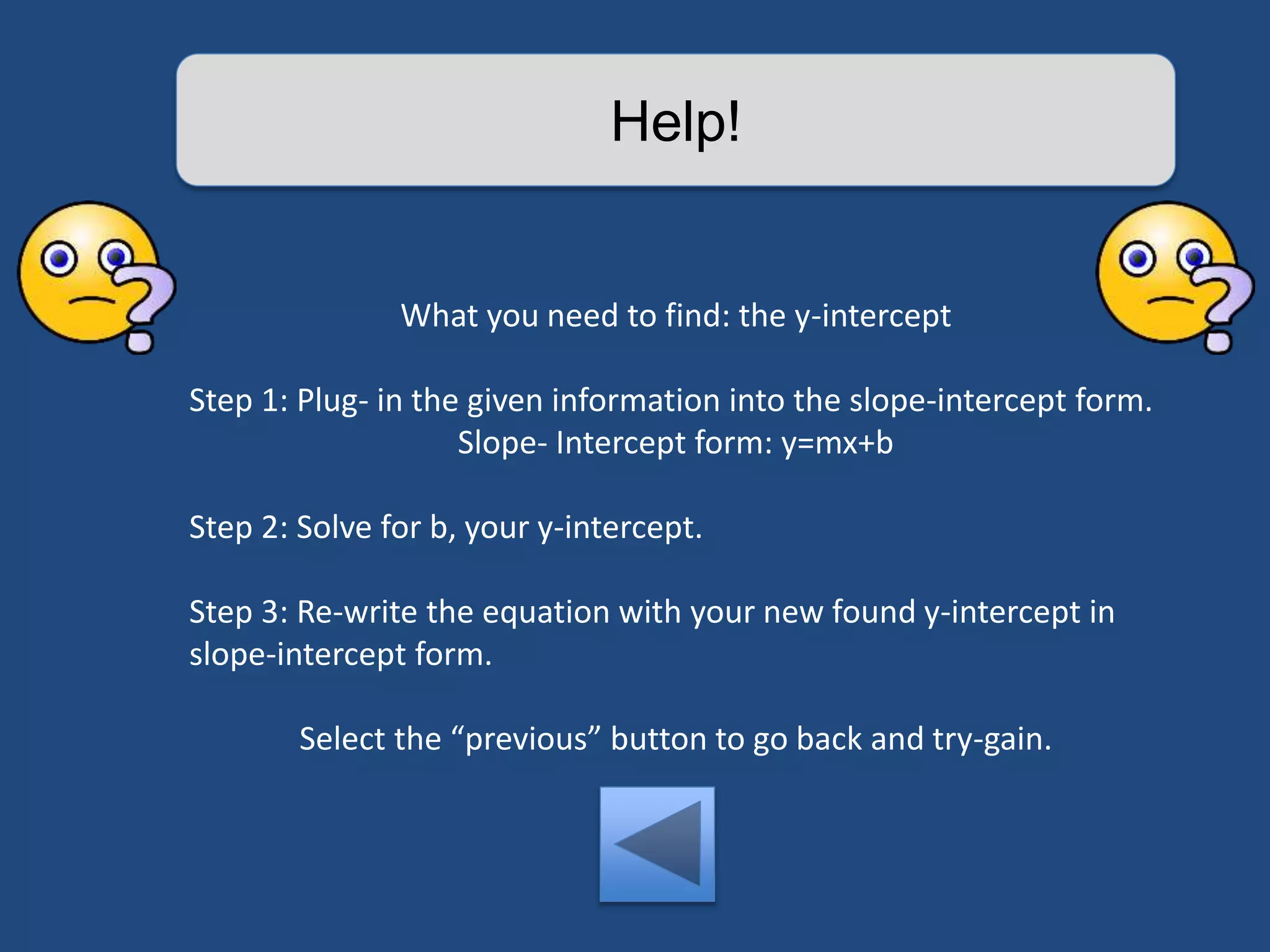
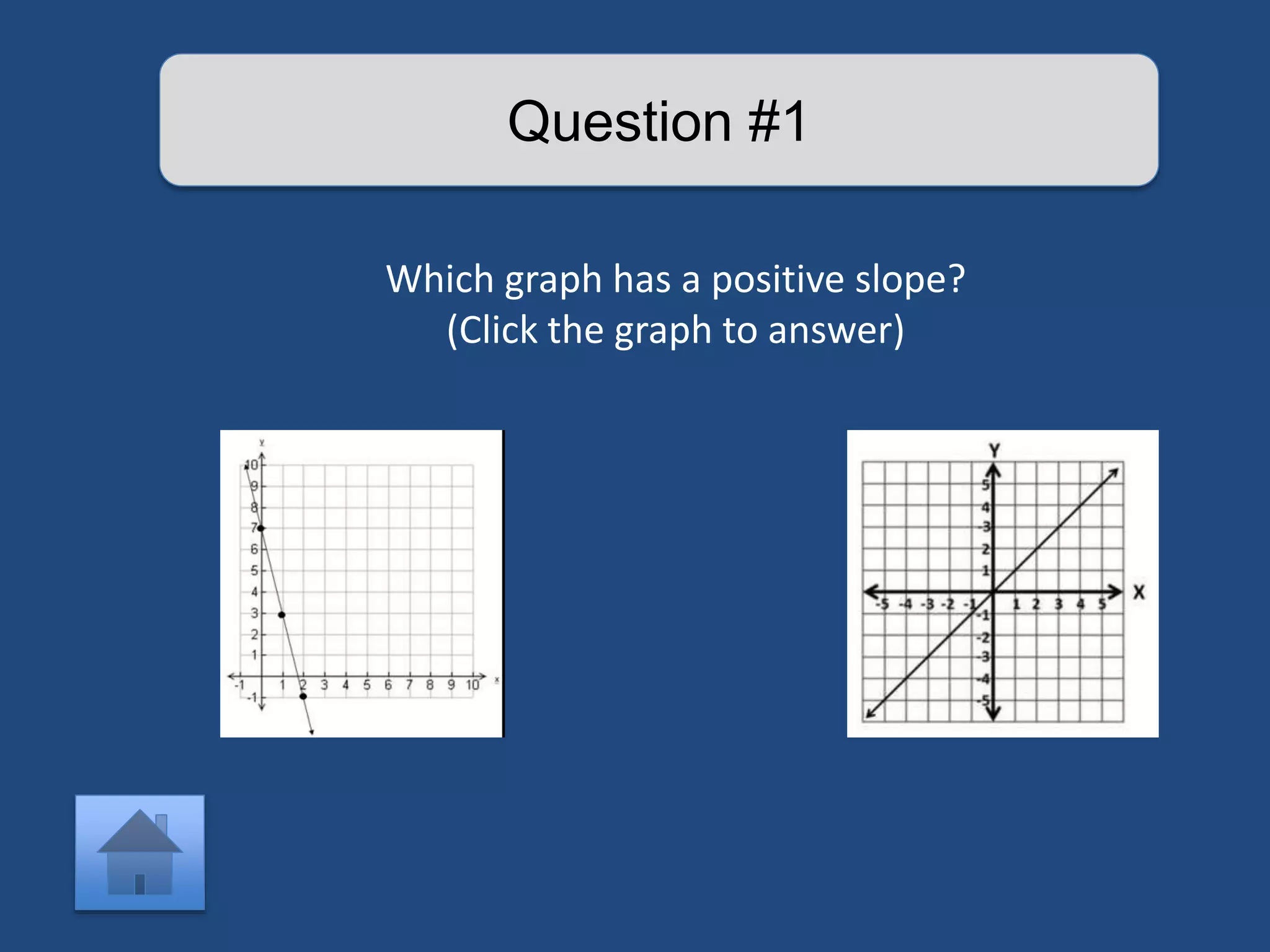
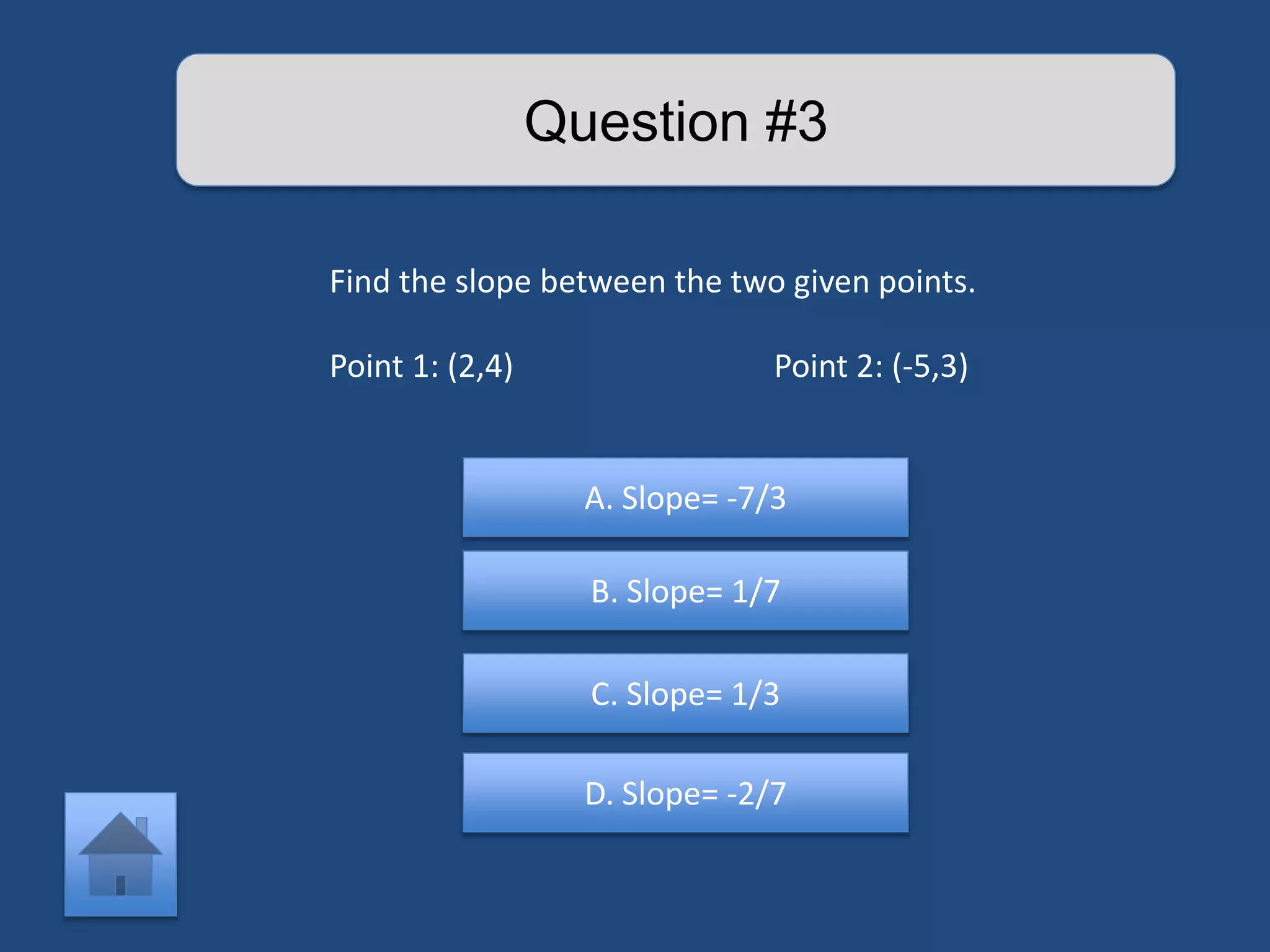
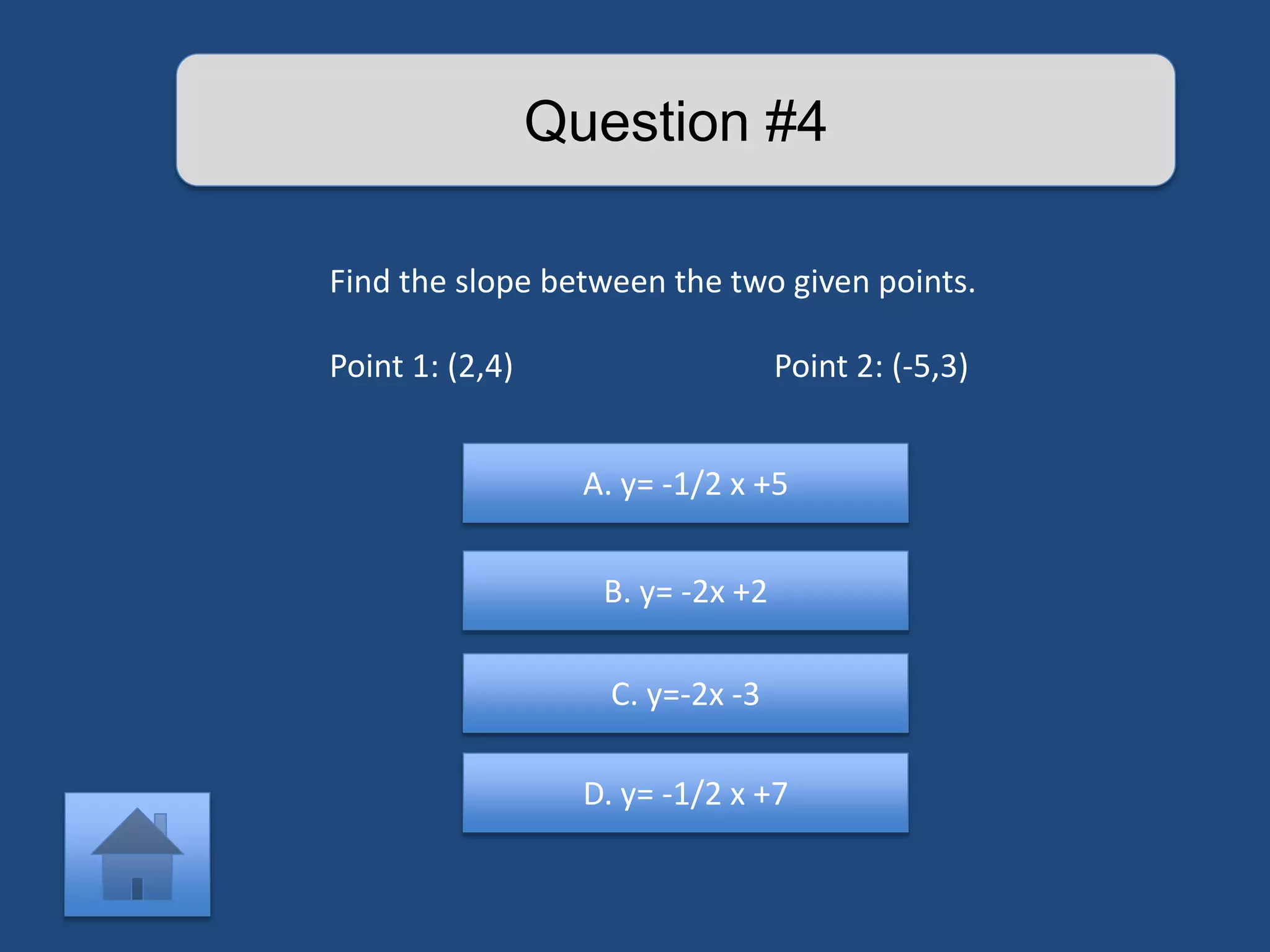
The document provides an interactive lesson on linear equations, covering slope-intercept form, how to find slope, and how to write linear equations. It outlines the concepts with definitions and examples, including quizzes for assessment. The lesson promotes learning through practice and review, guiding the user through different concepts with prompts for interaction.