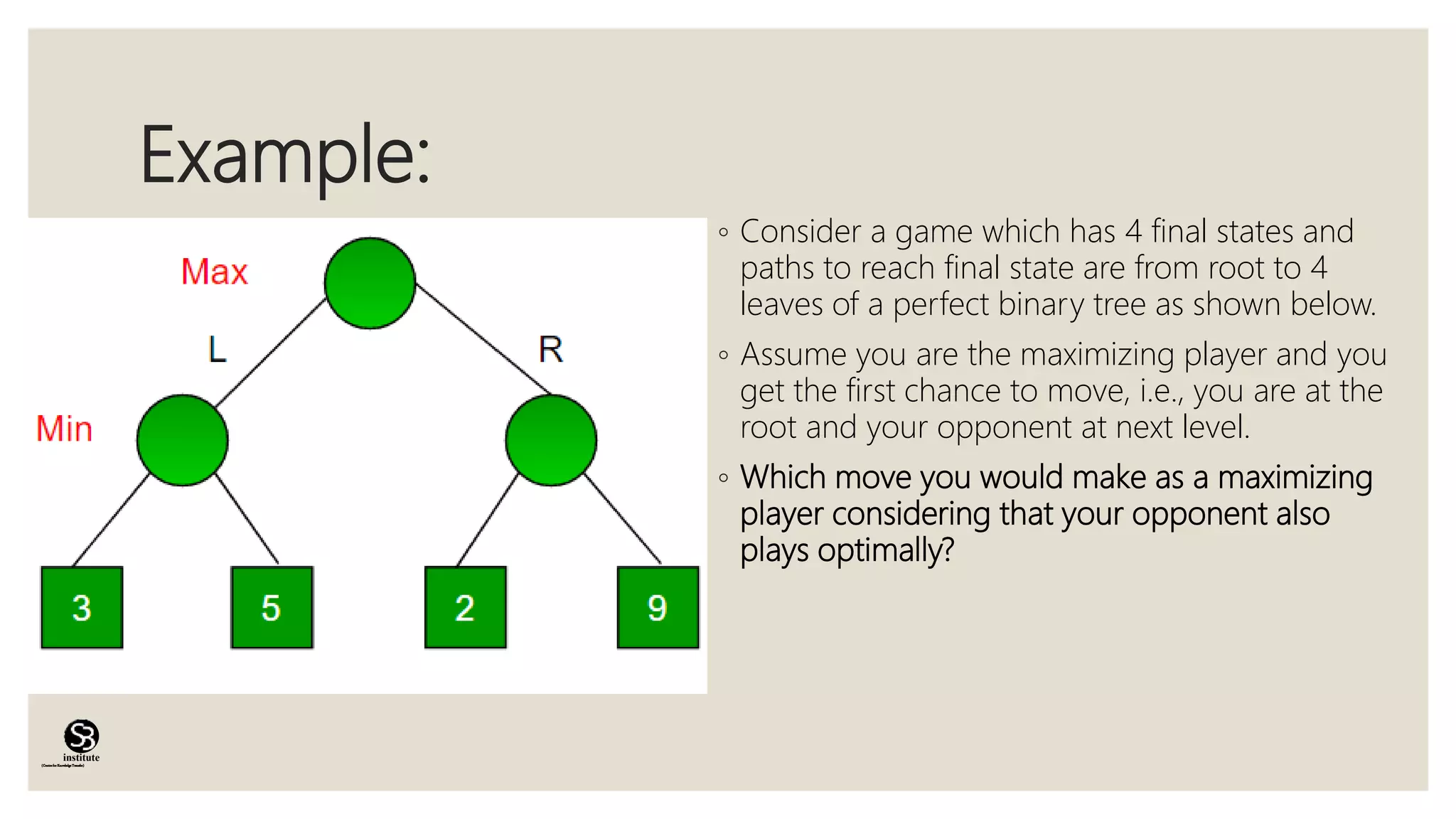
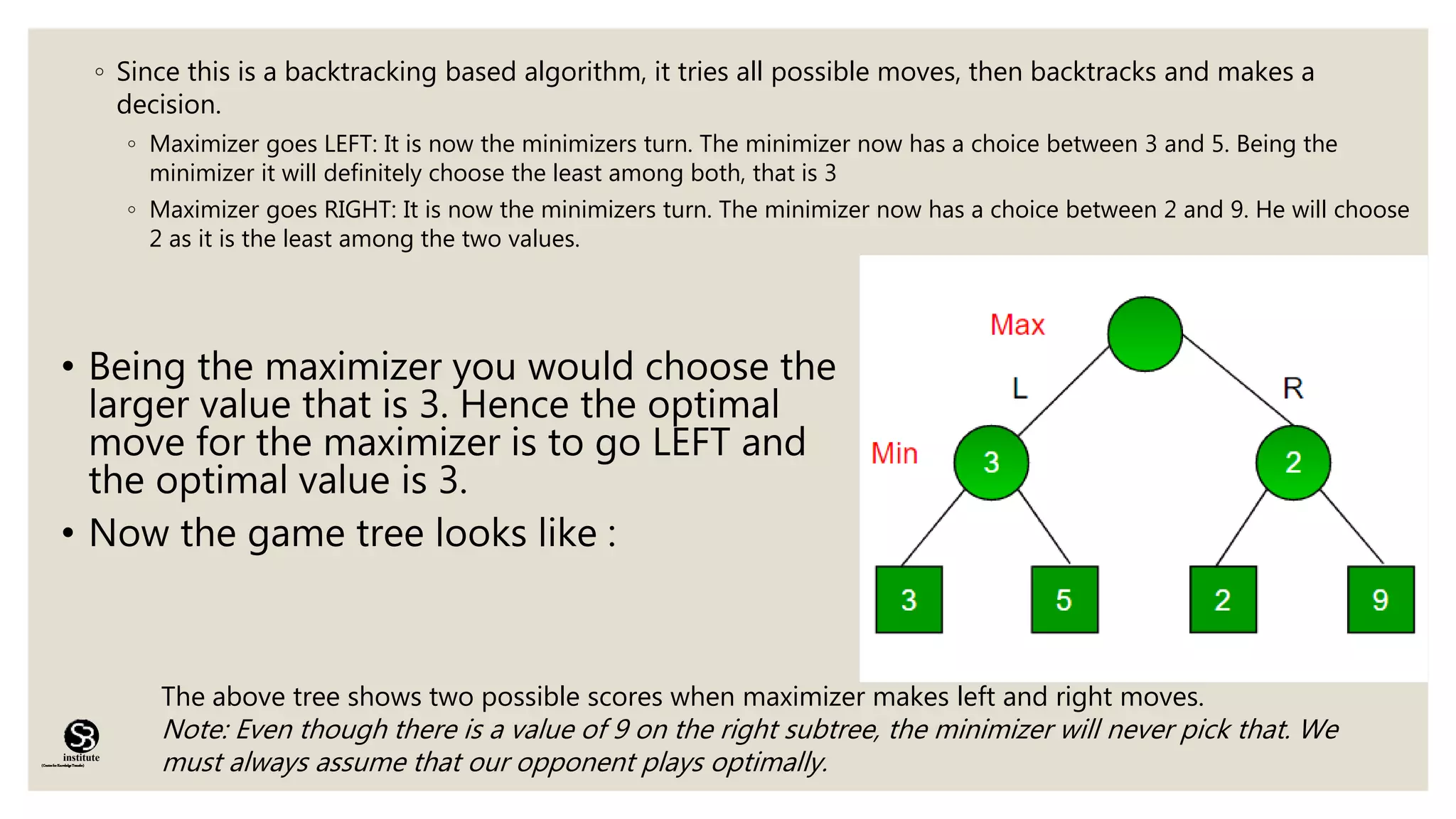
The minmax algorithm is used in two-player turn-based games to determine the optimal move for a player assuming the opponent plays optimally. It works by having one player act as the maximizer trying to maximize their score, and the other as the minimizer trying to minimize the score. The algorithm analyzes all possible moves and countermoves to determine the outcome with the best score for the maximizer. It is optimal if both players play optimally but has limitations due to its exhaustive search of all possibilities.