Download as PDF, PPTX
More Related Content
![SSII2021 [OS2-01] 転移学習の基礎：異なるタスクの知識を利用するための機械学習の方法](https://cdn.slidesharecdn.com/ss_thumbnails/os2-02final-210610091211-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
Similar to 数式を綺麗にプログラミングするコツ #spro2013
![[Yang, Downey and Boyd-Graber 2015] Efficient Methods for Incorporating Knowl...](https://cdn.slidesharecdn.com/ss_thumbnails/sparse-constrained-lda-151024072334-lva1-app6891-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
![ACL2014 Reading: [Zhang+] "Kneser-Ney Smoothing on Expected Count" and [Pickh...](https://cdn.slidesharecdn.com/ss_thumbnails/kneser-neyacl2014-140711113350-phpapp02-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
![[Kim+ ICML2012] Dirichlet Process with Mixed Random Measures : A Nonparametri...](https://cdn.slidesharecdn.com/ss_thumbnails/dp-mrmkimicml2012-120727233419-phpapp01-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
![[Karger+ NIPS11] Iterative Learning for Reliable Crowdsourcing Systems](https://cdn.slidesharecdn.com/ss_thumbnails/karger-croudsourcing-nips11-120408005300-phpapp01-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
数式を綺麗にプログラミングするコツ #spro2013
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7. この後の流れ 1. 数式がそこにあった – 「式はどうやって出てきたか」は考慮しない 2.数式を読み解く 3. 数式を書き換える 4. 数式を「逐語訳」で実装
- 8. 対象とする「数式」 • 行列やその要素の掛け算が出てくる数式 – 機械学習などの手法には、行列を使って表さ れているものが多い –強力な線形代数ライブラリをうまく使えば楽 に実装できる • 数式の例はC.M.ビショップ「パターン認 識と機械学習」(以降 PRML)から採用 – ただし機械学習の知識は一切要求しない
- 9. 方針 • 「楽に」「確実に」実装しよう – 間違いにくく、可読性が高い –最速は必ずしも目指していない • 動くものを確かに作れるようになってから • Python/numpy と R での実装例を紹介 – 基本的な行列計算しか使わないので、その他 の環境(Eigen など)にも参考になる（はず）
- 10.
- 11. まずは一番簡単なパターンから 𝒘 = 𝚽𝑇 𝚽 −1 𝚽 𝑇 𝒕 (PRML 3.15 改) • 線形回帰のパラメータ推定の式 – 「線形回帰とは何か」などは一切気にせず、 この式を実装することのみ考える
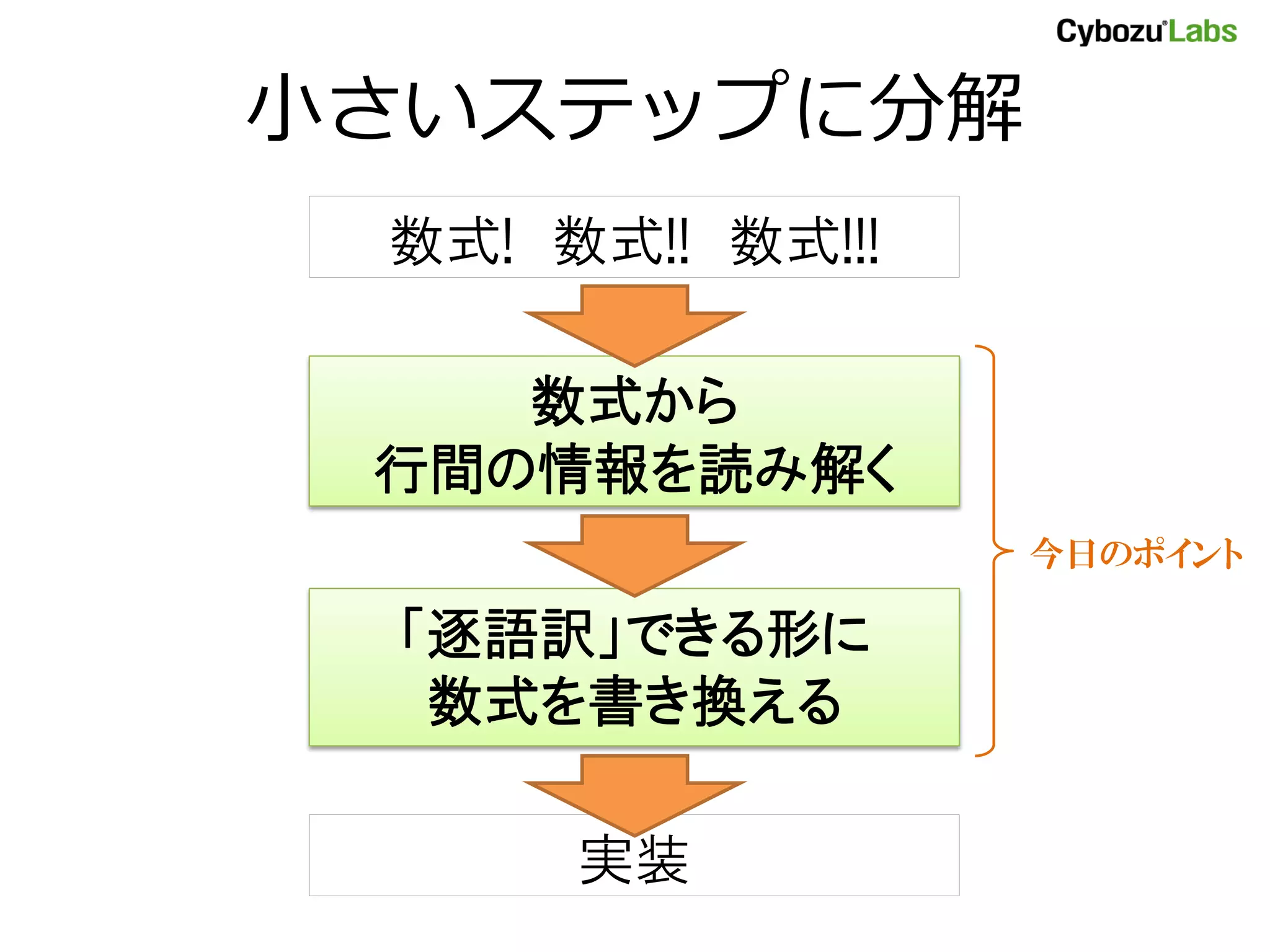
- 12. 数式の「読み解き」 𝒘 = 𝚽𝑇 𝚽 −1 𝚽 𝑇 𝒕 (PRML 3.15 改) • 𝚽：N×M次元の特徴行列 – 「特徴行列とは?」は気にしない – 「N×M次元の行列」ということだけ • t：N次のベクトル(正解データ) – 中身は気にしない(以下同様) • w はベクトル？ 行列？ 何次の？
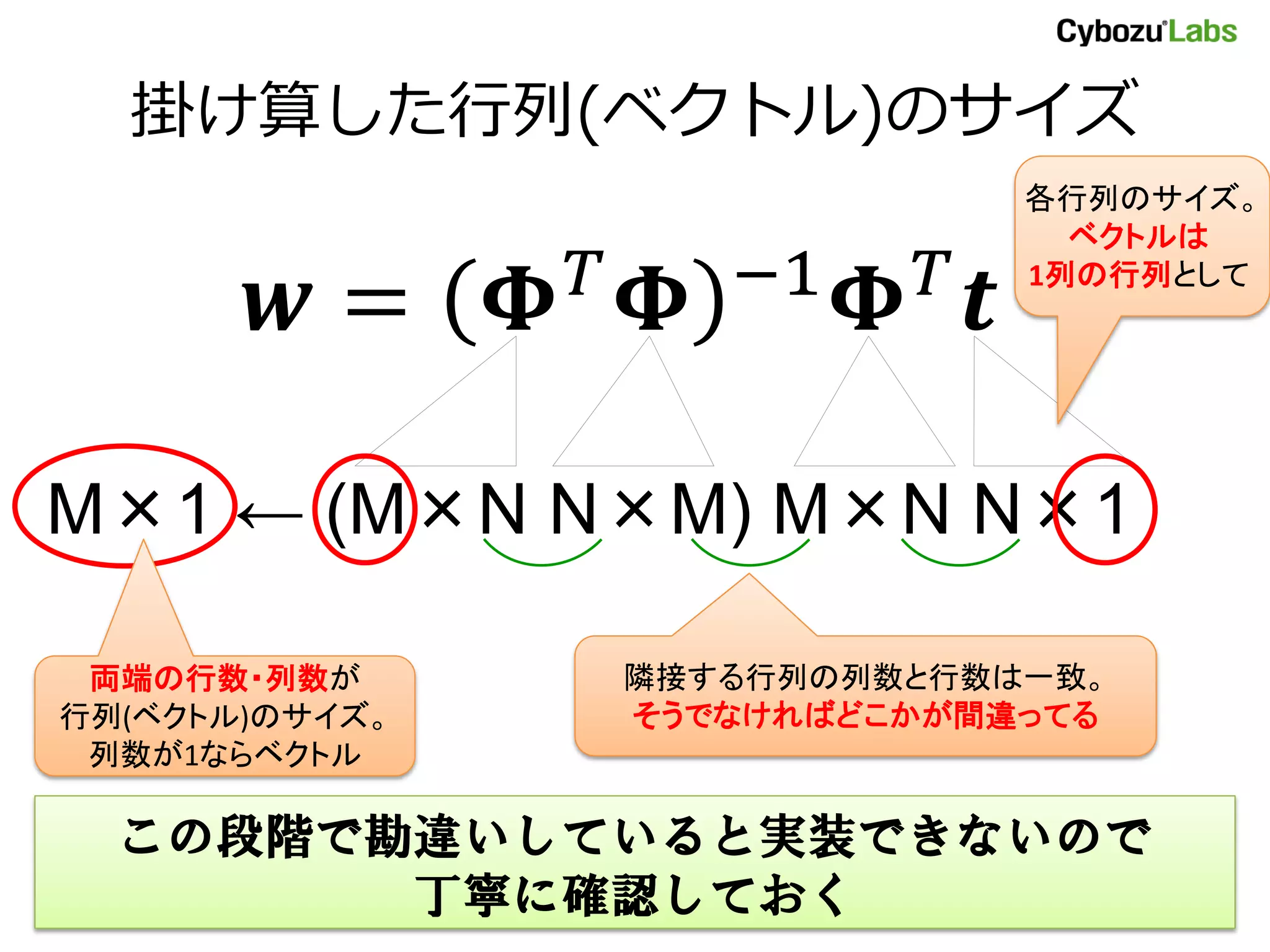
- 13. 掛け算した行列(ベクトル)のサイズ 𝒘 = 𝚽𝑇 𝚽 −1 𝚽 𝑇 𝒕 M×1 ← (M×N N×M) M×N N×1 隣接する行列の列数と行数は一致。 そうでなければどこかが間違ってる 各行列のサイズ。 ベクトルは 1列の行列として この段階で勘違いしていると実装できないので 丁寧に確認しておく 両端の行数・列数が 行列(ベクトル)のサイズ。 列数が1ならベクトル
- 14. numpy に「逐語訳」 𝒘 =𝚽 𝑇 𝚽 −1 𝚽 𝑇 𝒕 (PRML 3.15 改) # PHI = N×M次元の特徴行列 # t = N次のベクトル(正解データ) w = numpy.linalg.solve(numpy.dot(PHI.T, PHI), numpy.dot(PHI.T, t)) ※ 逆行列のところで inv() を使ってもいいが solve() の方がコードが短く、速度も速い numpy.dot(PHI.T, PHI) numpy.dot(PHI.T, t) 𝑨−1 𝒃 = numpy.linalg.solve(𝑨, 𝒃)
- 15. R に「逐語訳」 𝒘 =𝚽 𝑇 𝚽 −1 𝚽 𝑇 𝒕 (PRML 3.15 改) # PHI = N×M次元の特徴行列 # T = N次のベクトル(正解データ) w <- solve(t(PHI) %*% PHI, t(PHI) %*% T) # crossprod(X) = t(X) %*% X 関数を使っても良い w <- solve(crossprod(PHI), crossprod(PHI, T)) t(PHI) %*% PHI t(PHI) %*% T 𝑨−1 𝒃 = solve(𝑨, 𝒃)
- 16.
- 17. 多クラスロジスティック回帰の 誤差関数の勾配 𝛻𝒘 𝑘 𝐸 𝑾= 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝝓 𝑛 𝑁 𝑛=1 (k = 1, ⋯ , 𝐾) (PRML 4.109 改) • 𝒀 = 𝑦 𝑛𝑘 : N×K 次行列(予測値) • 𝑻 = 𝑡 𝑛𝑘 : N×K 次行列(1-of-K 表現) • 𝑾 = 𝒘1, … , 𝒘 𝐾 = (𝑤 𝑚𝑘) : M×K 次行列 • 𝚽 = 𝜙 𝑛𝑚 = 𝝓1, ⋯ , 𝝓 𝑁 𝑇 : N×M 次行列 – 𝝓 𝑛 = 𝝓 𝒙 𝑛 = 𝜙 𝑚 𝒙 𝑛 𝑇: M 次ベクトル 与 え ら れ て い る 情 報 実装に関係する のはサイズだけ
- 18. 「勾配」の扱い 𝛻𝒘 𝑘 𝐸 𝑾= 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝝓 𝑛 𝑁 𝑛=1 • 右辺は M 次ベクトル – 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 はただのスカラー – 一般には先ほどの方法で次元を読み解けばいい • だから左辺 𝛻𝒘 𝑘 𝐸 𝑾 も M 次ベクトル – それが k=1,……,K 個あるだけ • 「M×K次元の行列 𝛻𝐸 𝑾 」を求めると読み解く – 「勾配」そのものは実装には関係ない これ
- 19. 「逐語訳」できる形に書き換える • 掛けて行列になるパターンは大きく3通り – 上から要素積、行列積、直積 𝑐𝑖𝑗= 𝑎𝑖𝑗 𝑏𝑖𝑗 ⇔ C = A * B 𝑐𝑖𝑗 = 𝑎𝑖𝑘 𝑏 𝑘𝑗𝑘 ⇔ C=numpy.dot(A, B) 𝑐𝑖𝑗 = 𝑎𝑖 𝑏𝑗 ⇔ C=numpy.outer(a, b) 数式を左の形に書き換えれば、 右の numpy コードに「逐語訳」できる ※他に「外積」もあるが、使う人やシーンが限られるので略
- 20. R 版「逐語訳」 • 掛けて行列になるパターンは大きく3通り –上から要素積、行列積、直積 𝑐𝑖𝑗 = 𝑎𝑖𝑗 𝑏𝑖𝑗 ⇔ C <- A * B 𝑐𝑖𝑗 = 𝑎𝑖𝑘 𝑏 𝑘𝑗𝑘 ⇔ C <- A %*% B 𝑐𝑖𝑗 = 𝑎𝑖 𝑏𝑗 ⇔ C <- outer(a, b) ※直積は outer(a, b) の他に a %o% b という書き方もある
- 21. 式を書き換える (1) 𝛻𝒘 𝑘 𝐸𝑾 = 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝝓 𝑛 𝑁 𝑛=1 • 行列の要素の式になおす 𝛻𝐸 𝑾 𝑚𝑘 = 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝜙 𝑛𝑚 𝑁 𝑛=1 (𝑚 = 1, ⋯ , 𝑀; 𝑘 = 1, ⋯ , 𝐾) – 「求める行列𝛻𝐸 𝑾 」の (m, k) 成分の式にする M次ベクトルの式 スカラー
- 22. 式を書き換える (2) 𝛻𝐸 𝑾𝑚𝑘 = 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝜙 𝑛𝑚 𝑁 𝑛=1 • 注：右辺の添え字に未解決のものは残らない – 左辺に現れる : m, k – 右辺で解決 : n (総和で消える) • ３種類の積のどれかに帰着するよう変形 – この場合、総和があるので 𝑐𝑖𝑗 = 𝑎𝑖𝑘 𝑏 𝑘𝑗𝑘 に
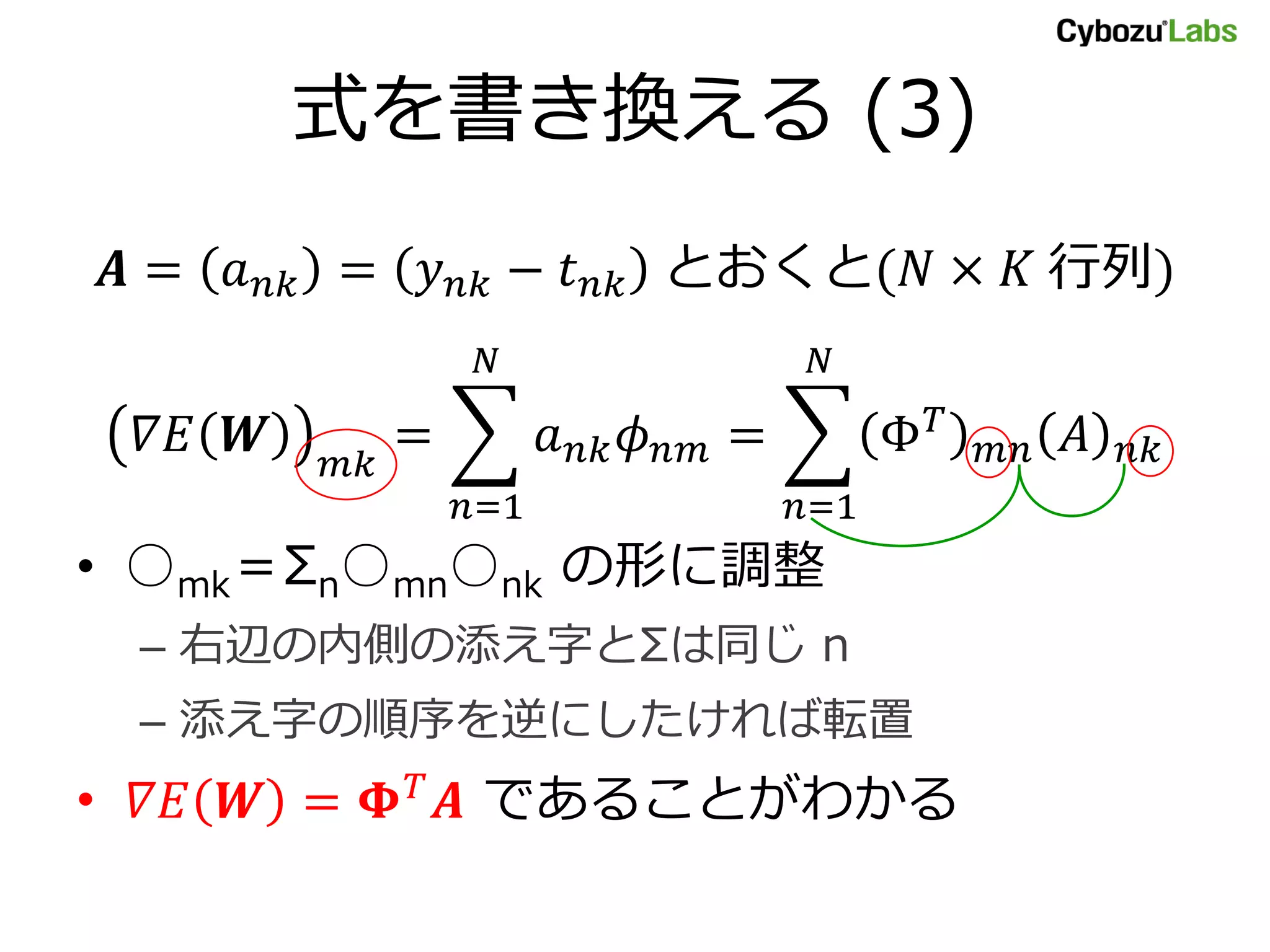
- 23. 式を書き換える (3) 𝑨 =𝑎 𝑛𝑘 = 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 とおくと(𝑁 × 𝐾 行列) 𝛻𝐸 𝑾 𝑚𝑘 = 𝑎 𝑛𝑘 𝜙 𝑛𝑚 𝑁 𝑛=1 = Φ 𝑇 𝑚𝑛 𝐴 𝑛𝑘 𝑁 𝑛=1 • ○mk＝Σn○mn○nk の形に調整 – 右辺の内側の添え字とΣは同じ n – 添え字の順序を逆にしたければ転置 • 𝛻𝐸 𝑾 = 𝚽 𝑇 𝑨 であることがわかる
- 24. numpyに「逐語訳」 𝛻𝒘 𝑘 𝐸 𝑾= 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝝓 𝑛 (k = 1, ⋯ , 𝐾) 𝑁 𝑛=1 𝑨 = 𝒀 − 𝑻, 𝛻𝐸 𝑾 = 𝚽 𝑇 𝑨 • ここまで簡単になれば、実装は一瞬 # PHI = N×M 次元の特徴行列 # Y, T = N×K 次元の行列 gradient_E = numpy.dot(PHI.T, Y - T) 式の書き換え
- 25. R に「逐語訳」 𝛻𝒘 𝑘 𝐸𝑾 = 𝑦 𝑛𝑘 − 𝑡 𝑛𝑘 𝝓 𝑛 (k = 1, ⋯ , 𝐾) 𝑁 𝑛=1 𝑨 = 𝒀 − 𝑻, 𝛻𝐸 𝑾 = 𝚽 𝑇 𝑨 • 同様に R での実装例: # PHI = N×M 次元の特徴行列 # Y, T = N×K 次元の行列 gradient_E <- t(PHI) %*% (Y - T)
- 26. まとめ • 数式から条件を読み解こう – この段階で間違っていると、うまく行かない –さぼらず紙と鉛筆で確認するのが一番賢い • 「逐語訳」できる数式なら実装かんたん – 難しい数式は「逐語訳」できる形に書き換え – さぼらず紙と鉛筆