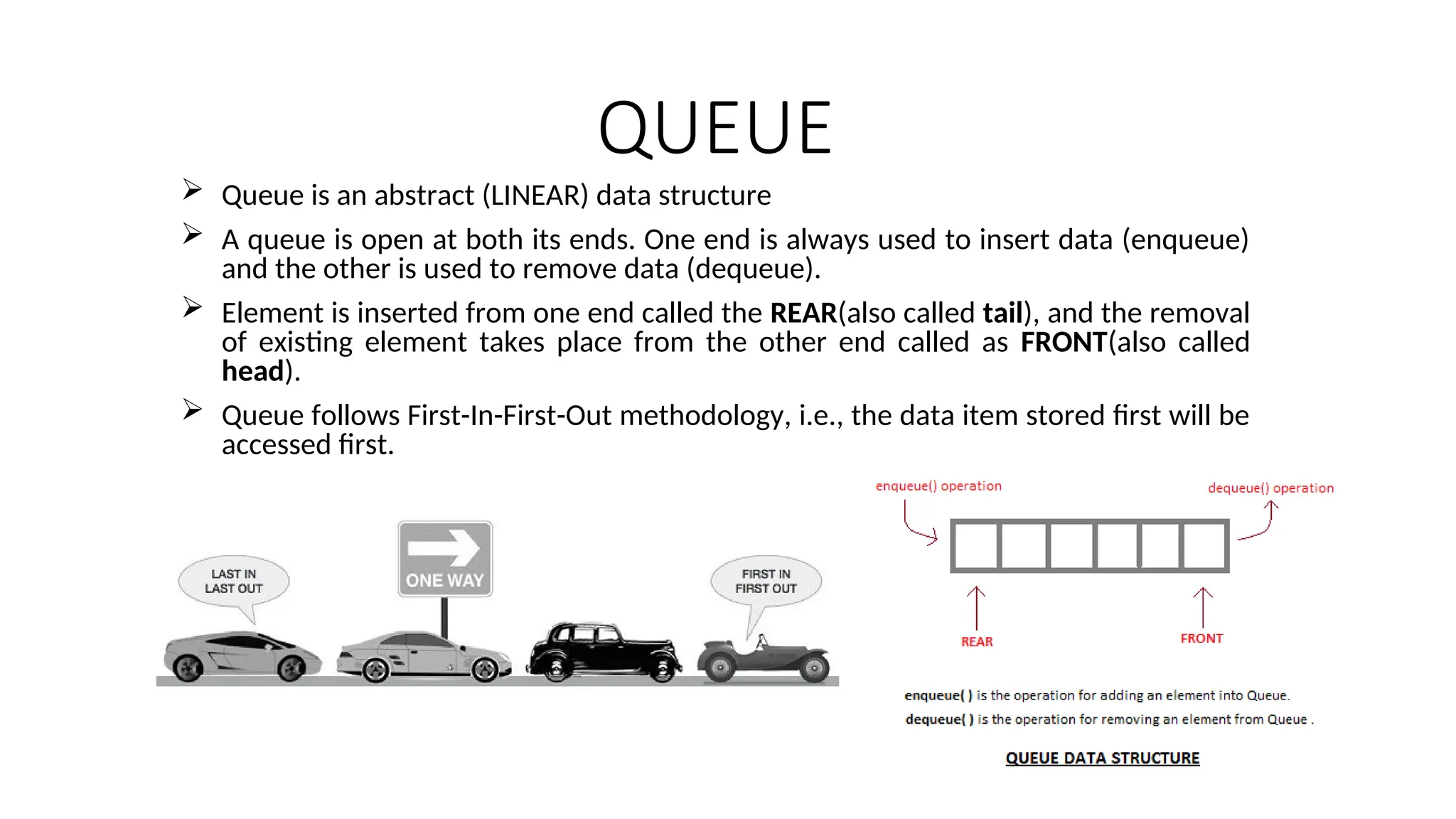
A queue is an abstract data structure that operates on a first-in-first-out (FIFO) basis, where elements are added from the rear and removed from the front. Key operations include enqueue (adding elements), dequeue (removing elements), and checking if the queue is empty or full, with several applications in CPU scheduling and real-time systems. Algorithms for both enqueue and dequeue operations are outlined, detailing conditions for overflow and underflow errors.





![Case 1:
A B c D e
F RN
F=1 R=5 N=5
Step 1: FRONT=1 and REAR=N
F=1 1=1 true &
REAR = N 5=5true OR
FRONT=REAR+1FRONT=6
Print Overflow
Case 2:
Let us the queue
Front F=1 R=3 N=5 ITEM=D
A B c
F R N
Step 1: FRONT=1 & REAR=N
FRONT=1 1=1 true &
REAR=N 3=5false OR
FRONT=REAR+11=4False
Step 2: FRONT=NULL FRONT=01=0false
Else if
REAR=N3=5false
Else
Set REAR=REAR+1REAR=3+1=4REAR=4
Step 3: QUEUE[REAR]= ITEM
QUEUE[4]=D
A B c D
F R N
Step 4: Exit](https://image.slidesharecdn.com/6-240910151153-543c3788/75/QUEUE-OPERATIONS-in-DATASTRUCTURE-AND-ALGORITHMS-7-2048.jpg)

![A
Case 1:
FR N
FRONT=1 REAR=1 N=5
Step 1: FRONT=-11=-1False
Step 2: Element=Queue[FRONT]
Element=Queue[1] Element=A
ADeleted
Step 3: FRONT=REAR1=1true
FRONT=REAR=-1
Step 4: Return
Case 2:
FRONT=-1 REAR=-1 N=5
Step 1: FRONT=-1-1=-
1true
Print “UNDERFLOW” & Return.
F=1 N=5 R=4
Case 3:
A B c d
F R N
Step 1: FRONT=-1 1=-1false
Step 2: Element=Queue[FRONT]
Element= Queue[1]Element=A
A deleted
B c d
F R N
Step 3: FRONT=REAR 1=4false
FRONT=FRONT+1FRONT=1+1=2
FRONT=2
B c d
F R N](https://image.slidesharecdn.com/6-240910151153-543c3788/75/QUEUE-OPERATIONS-in-DATASTRUCTURE-AND-ALGORITHMS-9-2048.jpg)