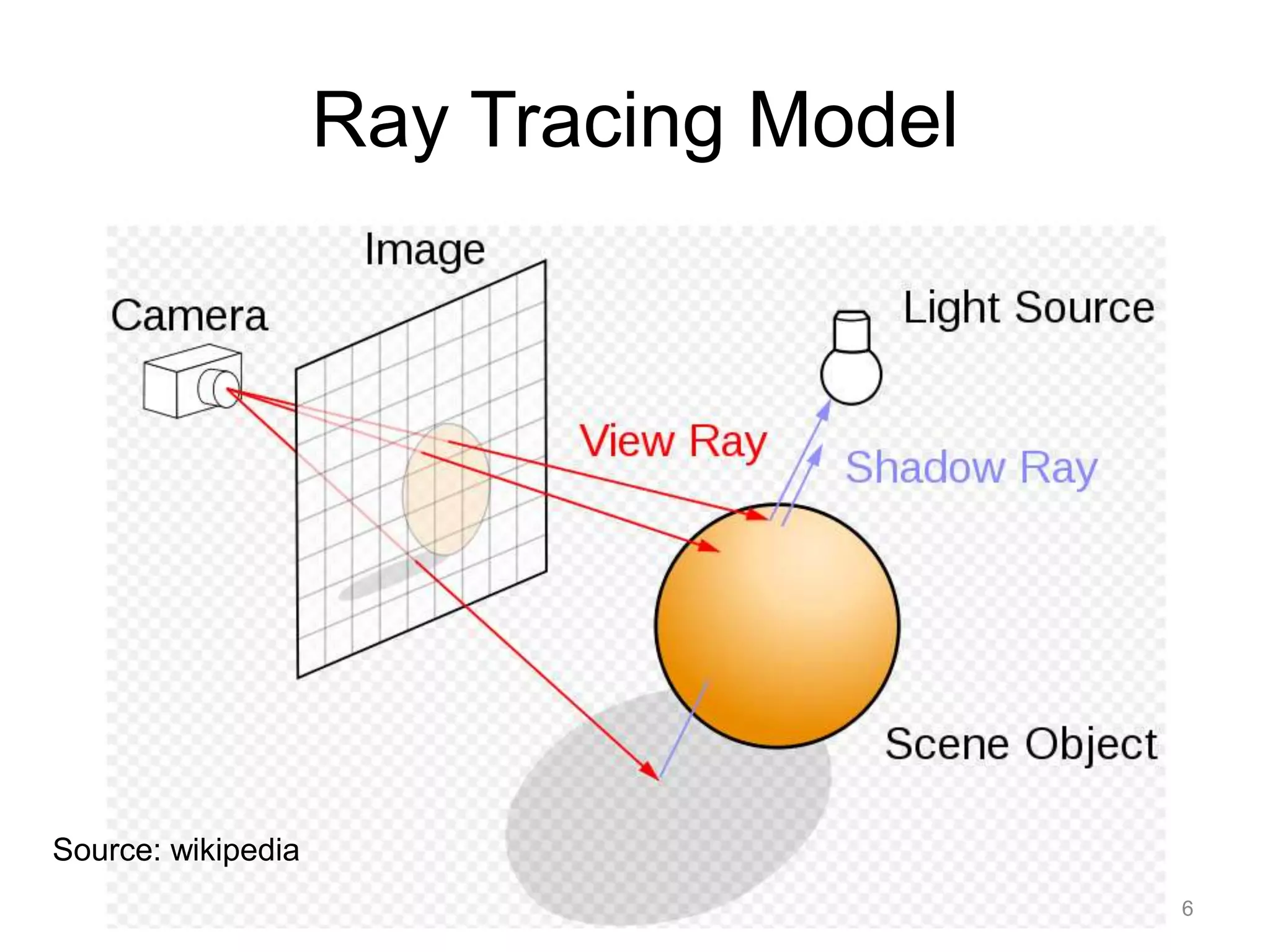
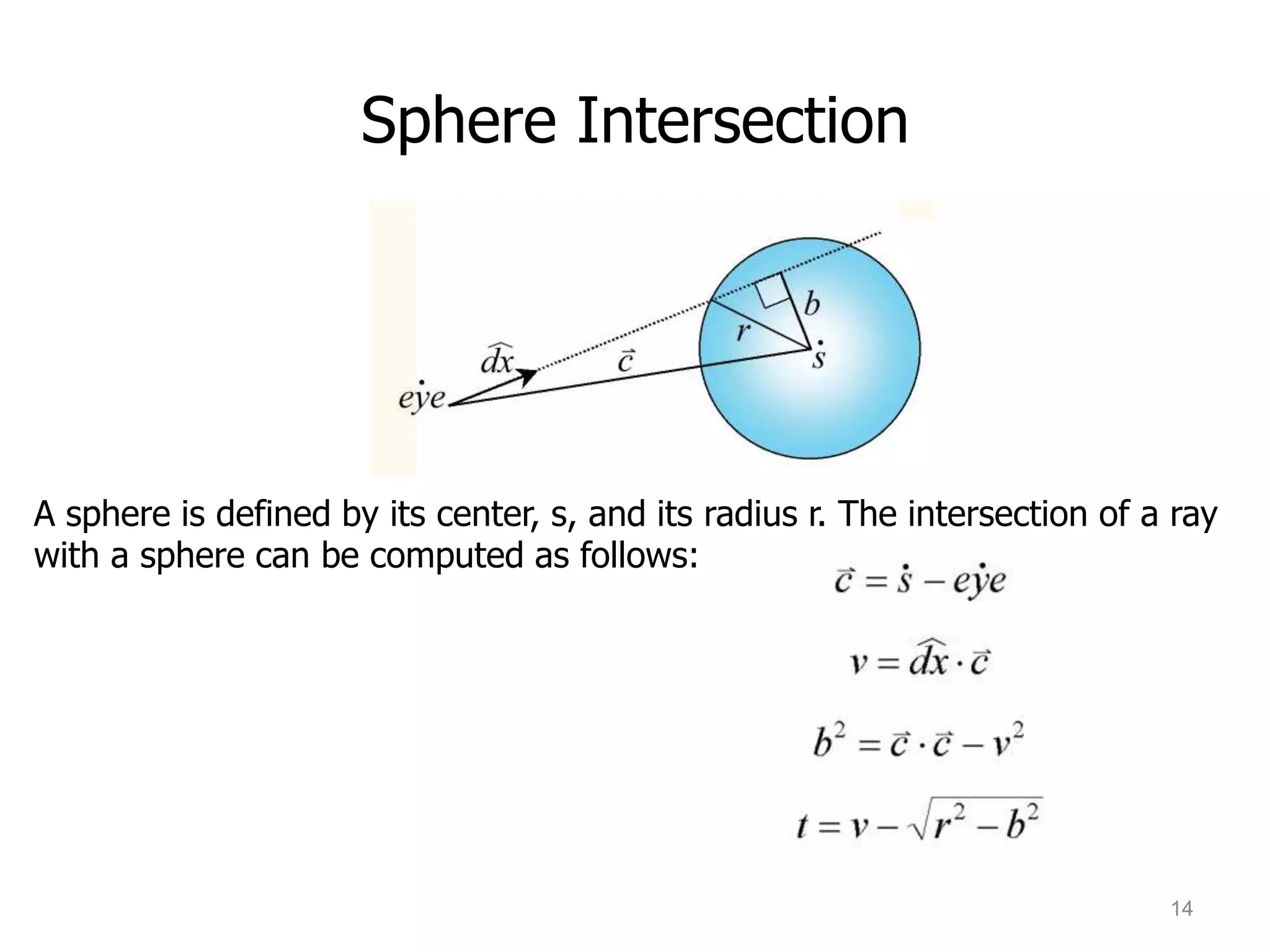
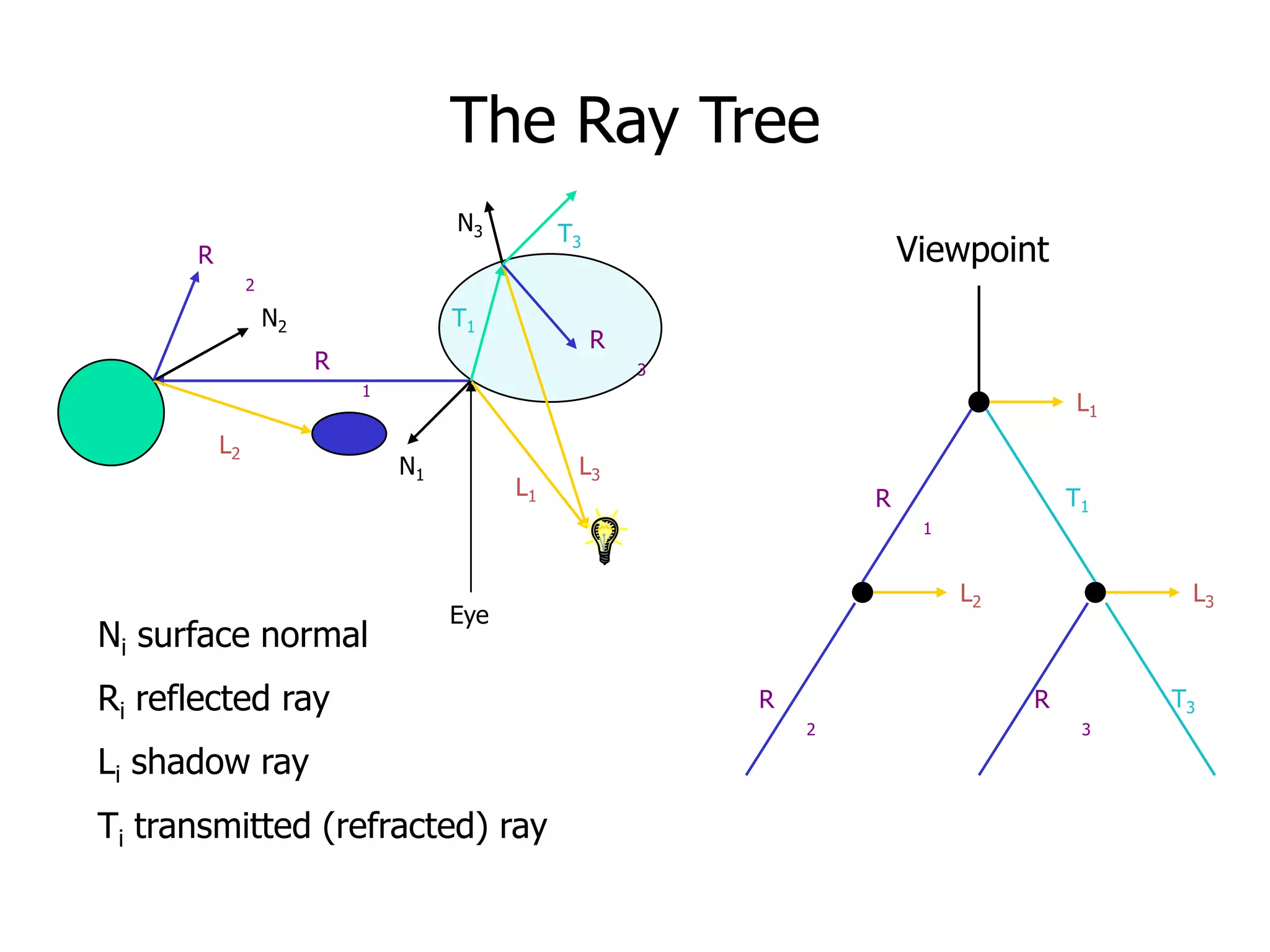
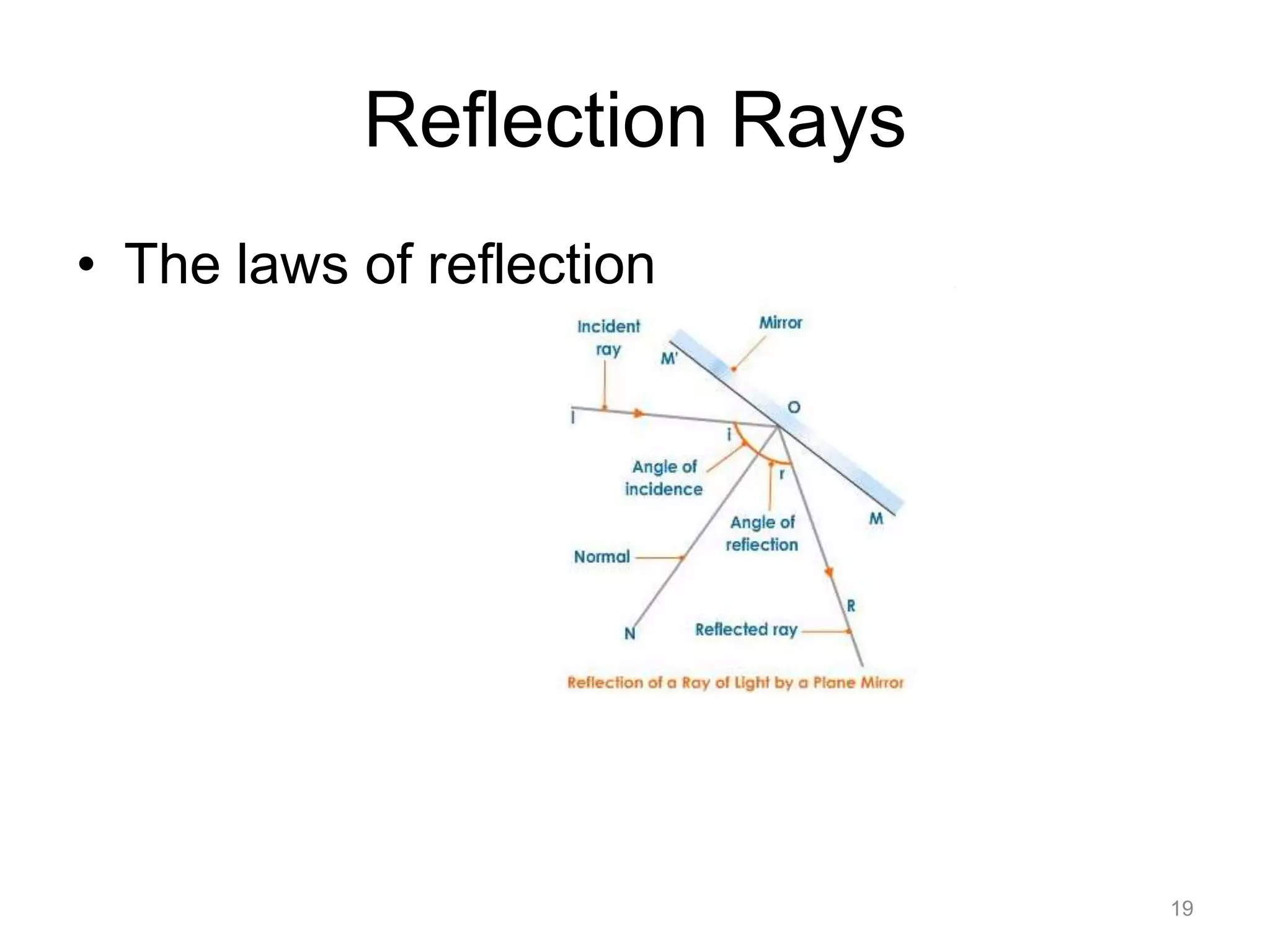
Ray tracing

What is ray tracing
• Ray tracing is a technique for rendering three-
dimensional graphics with very complex light
interactions. This means you can create pictures
full of mirrors, transparent surfaces, and shadows,
with stunning results.
• A very simple method to both understand and
implement.
• It is based on the idea that you can model
reflection and refraction by recursively following
the path that light takes as it bounces through an
environment

2

Raytraced Images

PCKTWTCH by K
evin Odhner, POV
-Ray
3

Kettle, Mike
Miller, POV-
Ray

4

Ray Tracing Model

Source: wikipedia
6

Ray tracing

Shadow rays

Reflection ray

refracted ray

7

Ray tracing algorithm
• Builds the image pixel by pixel
• Cast additional rays from the hit point to
determine the pixel color
– Shoot rays toward each light. If they hit
something, the object is shadowed from that light,
otherwise use “standard model” for the light
– Reflection rays for mirror surfaces, to see what
should be reflected in the mirror
– Refraction rays to see what can be seen through
transparent objects
– Sum all the contributions to get the pixel color

8

Recursive ray tracing
• When a reflected or refraction ray hits a
surface, repeat the whole process from that
point
– Send more out shadow rays
– Send out new reflected rays (if required)
– Send out a new refracted ray (if required)
– Generally, reduce the weight of each additional
ray when computing the contributions to the
surface color
– Stop when the contribution from a ray is too small
to notice or maximum recursion level has been
reached

9

Ray tracing implementation
• Ray tracing breakdown into two tasks
– Constructing the ray to cast
– Intersection rays with geometry
• The former problem is simple vector
arithmetic
• Intersection calculation can be done in
world coordinates or model coordinates

10

Constructing Rays
• Define rays by an initial point and a direction: x(t)=x0+td
• Eye rays: Rays from the eye through a pixel
– Construct using the eye location and the pixel’s location on the
image plane. X0 = eye
• Shadow rays: Rays from a point on a surface to the light.
– X0 = point on surface
• Reflection rays: Rays from a point on a surface in the reflection
direction
– Construct using laws of reflection. X0 = surface point
• Transmitted rays: Rays from a point on a transparent surface
through the surface
– Construct using laws of refraction. X0 = surface point

11

Ray-Object Intersections
• Aim: Find the parameter value, ti , at which the ray
first meets object i
• Write the surface of the object implicitly: f(x)=0
– Unit sphere at the origin is x•x-1=0
– Plane with normal n passing through origin is: n•x=0
• Put the ray equation in for x
– Result is an equation of the form f(t)=0 where we want t
– Now it’s just root finding

12

Ray-Sphere Intersection
Ray : x (t ) x0 td
Sphere : x x 1 0
Substitute: x0 td x0 td 1 0
: d d t2 2 x0 d t x0 x0 1 0
• Quadratic in t
– 2 solutions: Ray passes through sphere - take minimum
value that is > 0
– 1 solution: Ray is tangent - use it if >0
– 0 solutions: Ray does not hit sphere
• Numerical stability is very important. For example, can a
reflection ray hit the same sphere?

13

Sphere Intersection

A sphere is defined by its center, s, and its radius r. The intersection of a ray
with a sphere can be computed as follows:

14

Ray-Plane Intersections
Ray : x (t ) x0 td
P lane: n x 0
Substit ute: n x0 td 0
: n d t n x0 0
n x0
:t
n d

• This is plane going through the origin
– What about an arbitrary plane?
• To do polygons, intersect with plane then do point-in-polygon
test…

15

Intersections
• It is necessary to determine the
intersection between a ray with objects to
decide which pixel is
• Intersection with a sphere
• Intersection with a plane
• …

16

Ray Tracing Illumination
Recursive L R
E
ˆ
N
V Vreflected

I ( E, V ) I direct I reflected I transmitted I I reflected
P

I transmitted Vtransmitte d
I reflected k r I ( P,Vreflected )

I transmitted kt I ( P,Vtransmitted )

I direct k a I ambient I light ˆ ˆ
kd N L ks ˆ ˆ
V R
nshiny

Check for shadowing (intersection with object along ray (P,L))

The Ray Tree
N3 T3
R Viewpoint
2

N2 T1
R
R 3
1
L1
L2
N1 L3
L1 R T1
1

L2 L3
Eye
Ni surface normal
Ri reflected ray R R T3
2 3

Li shadow ray
Ti transmitted (refracted) ray

Reflection Rays
• The laws of reflection

19

Reflection
• Reflection angle = view angle

20

Reflection
• The maximum depth of the tree affects the handling of refraction
• If we send another reflected ray from here, when do we stop? 2
solutions (complementary)
– Answer 1: Stop at a fixed depth.
– Answer 2: Accumulate product of reflection coefficients and stop when
this product is too small.

21

Refraction
ˆ
N cos ˆ ˆ
I N
i
sin
Snell’s Law t i
ˆ
sin i t
r
ˆ
I N cos i
i ˆ
M
ˆ
T sin ˆ
M ˆ
cos t N
t

ˆ
( N cos ˆ
I)
ˆ
M i t
ˆ
sin ˆ
N T
i

ˆ sin t ˆ ˆ ˆ
T ( N cos i I ) cos t N Note that I is the negative of
sin i the incoming ray
ˆ
T ( cos ˆ
cos t ) N ˆ
I
r i r

cos ˆ ˆ
N I
i

cos 1 sin 2 1 2
sin 2 1 2 ˆ ˆ
(1 ( N I ) 2 )
t t r i r

Tˆ ˆ ˆ
(N I ) 1 2 ˆ ˆ ˆ
(1 ( N I ) 2 ) N ˆ
I
r r r

23

Shadow Rays
• Shadows are important lighting effect that
can be easily with ray tracing
• If we wish to compute the illinumination with
shadows for a point, we shoot an additional
ray from the point to every light source
• A light is only allowed to contribute to the final
color if the ray doesn’t hit anything between
the point and a light source

25

Pseudo Code for Ray Tracing
rgb lsou; // intensity of light source
rgb back; // background intensity
rgb ambi; // ambient light intensity

Vector L // vector pointing to light source
Vector N // surface normal
Object objects [n] //list of n objects in scene
float Ks [n] // specular reflectivity factor for each object
float Kr [n] // refractivity index for each object
float Kd [n] // diffuse reflectivity factor for each object
Ray r;

void raytrace() {
for (each pixel P of projection viewport in raster order) {
r = ray emanating from viewer through P
int depth = 1; // depth of ray tree consisting of multiple paths
the pixel color at P = intensity(r, depth)
}
}

26

rgb intensity (Ray r, int depth) {
Ray flec, frac;
rgb spec, refr, dull, intensity;

if (depth >= 5) intensity = back;
else {
find the closest intersection of r with all objects in scene
if (no intersection) {
intensity =back;
} else {
Take closest intersection which is object[j]
compute normal N at the intersection point
if (Ks[j] >0) { // non-zero specular reflectivity
compute reflection ray flec;
refl = Ks[j]*intensity(flec, depth+1);
} else refl =0;
if (Kr[j]>0) { // non-zero refractivity
compute refraction ray frac;
refr = Kr[j]*intensity(frac, depth+1);
} else refr =0;
check for shadow;
if (shadow) direct = Kd[j]*ambi
else direct = Phong illumination computation;
intensity = direct + refl +refr;
} }
return intensity; }

27

Thank for attention!

28

Ray tracing

More Related Content

What's hot

Similar to Ray tracing

Recently uploaded

Ray tracing