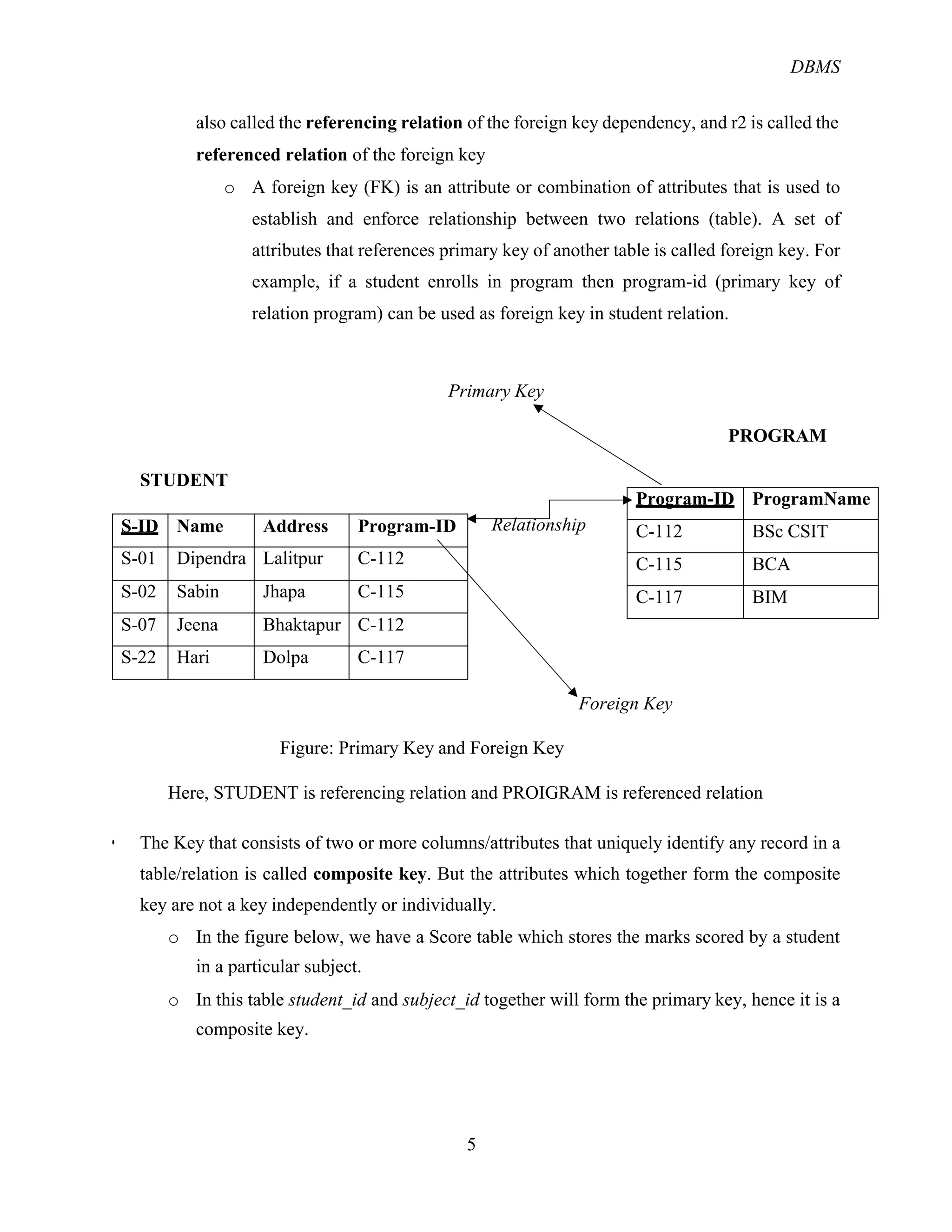
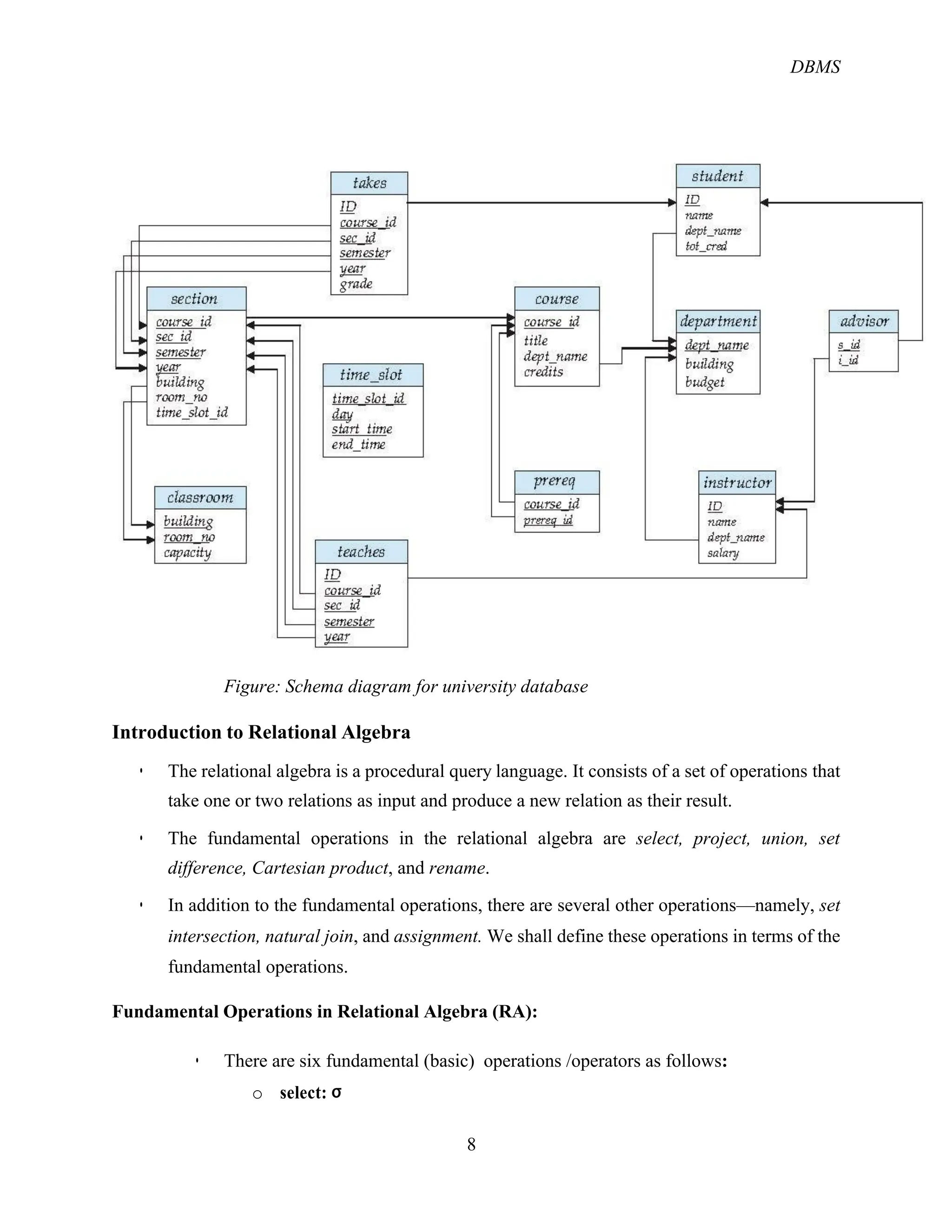
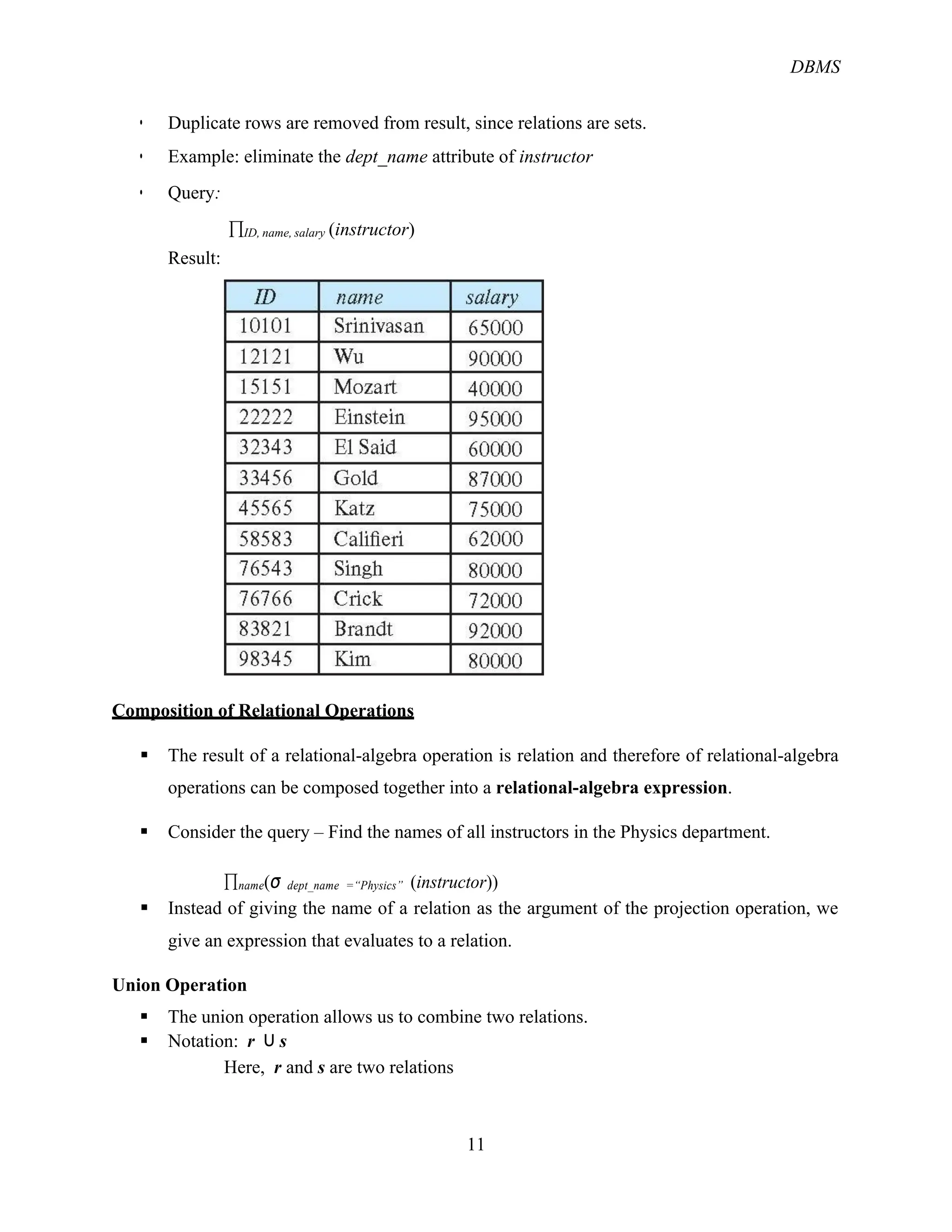
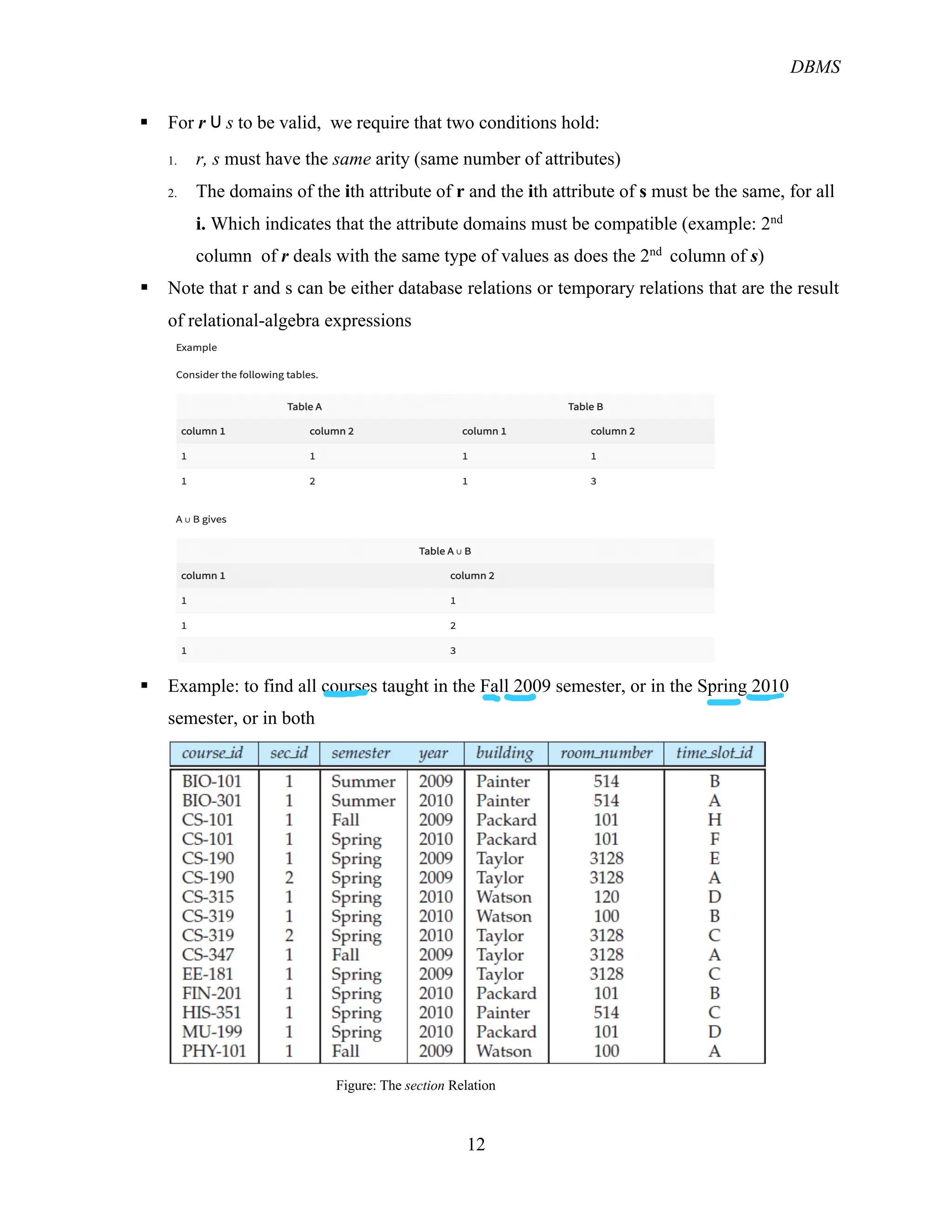
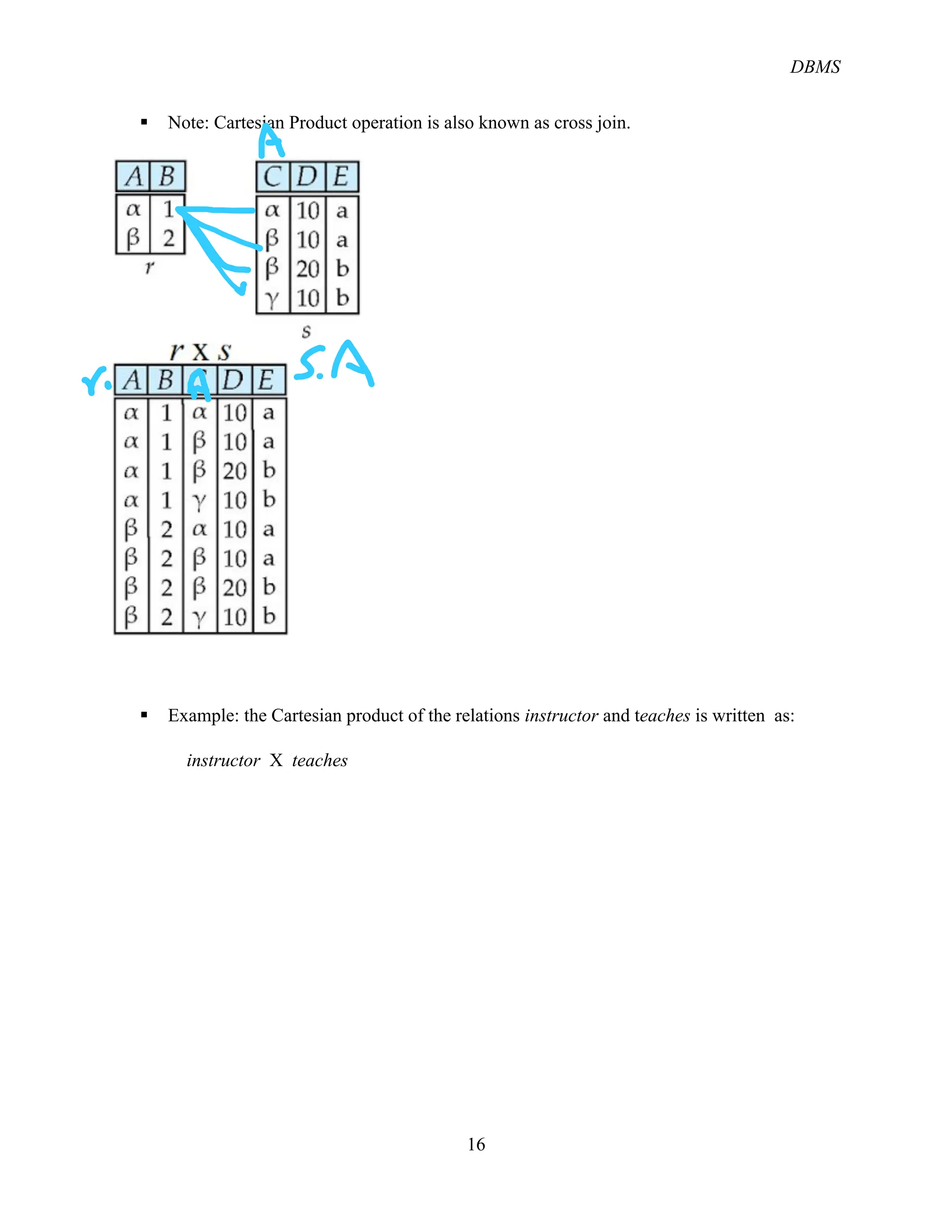
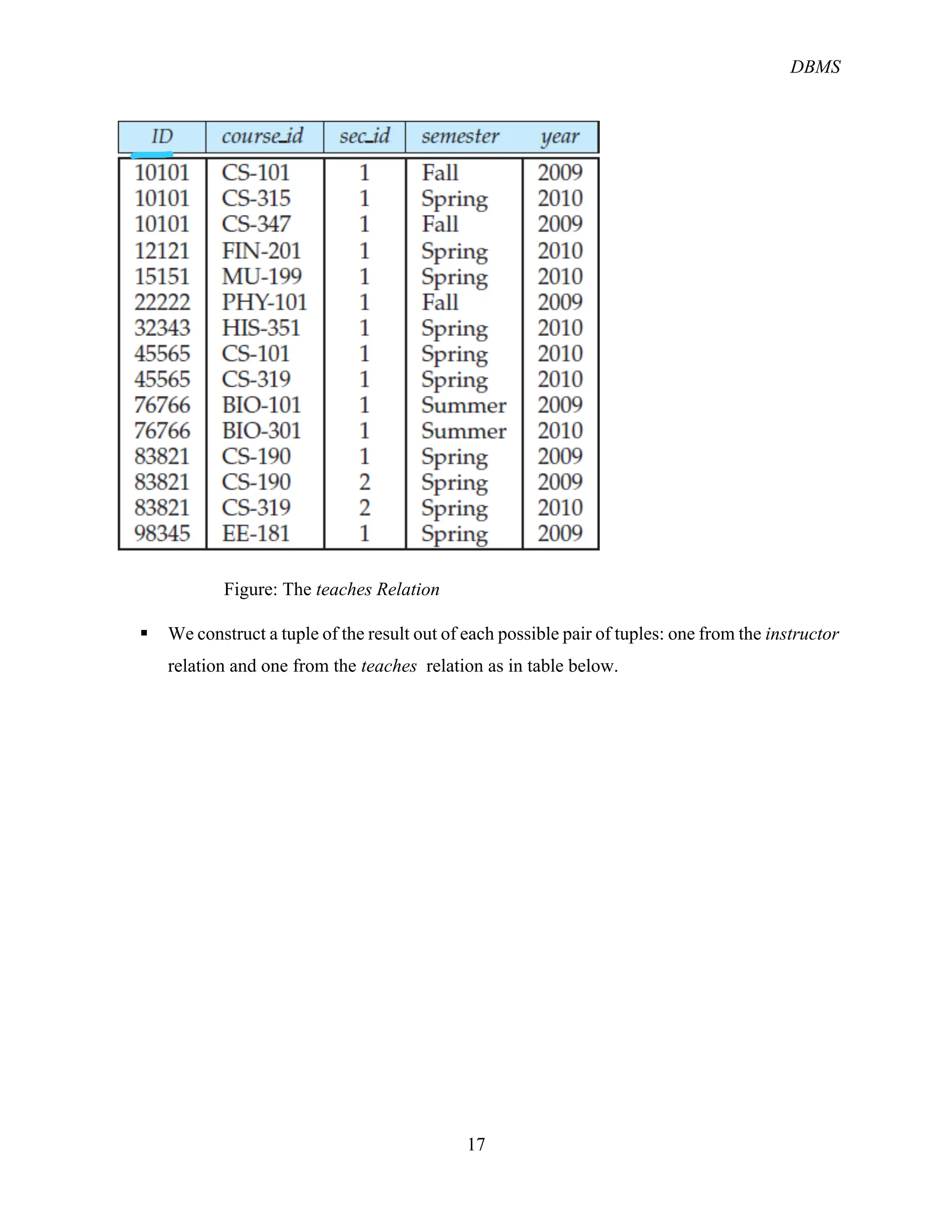
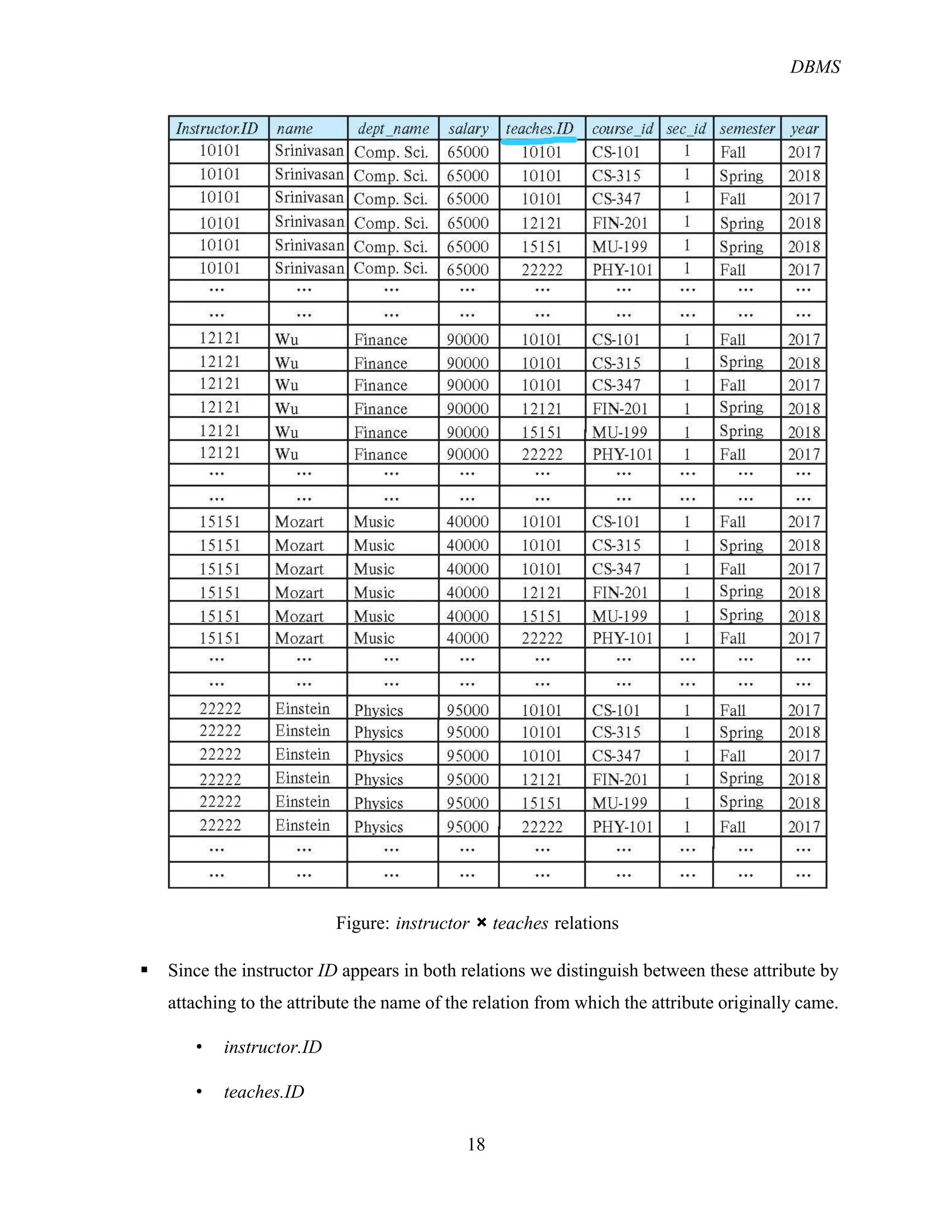
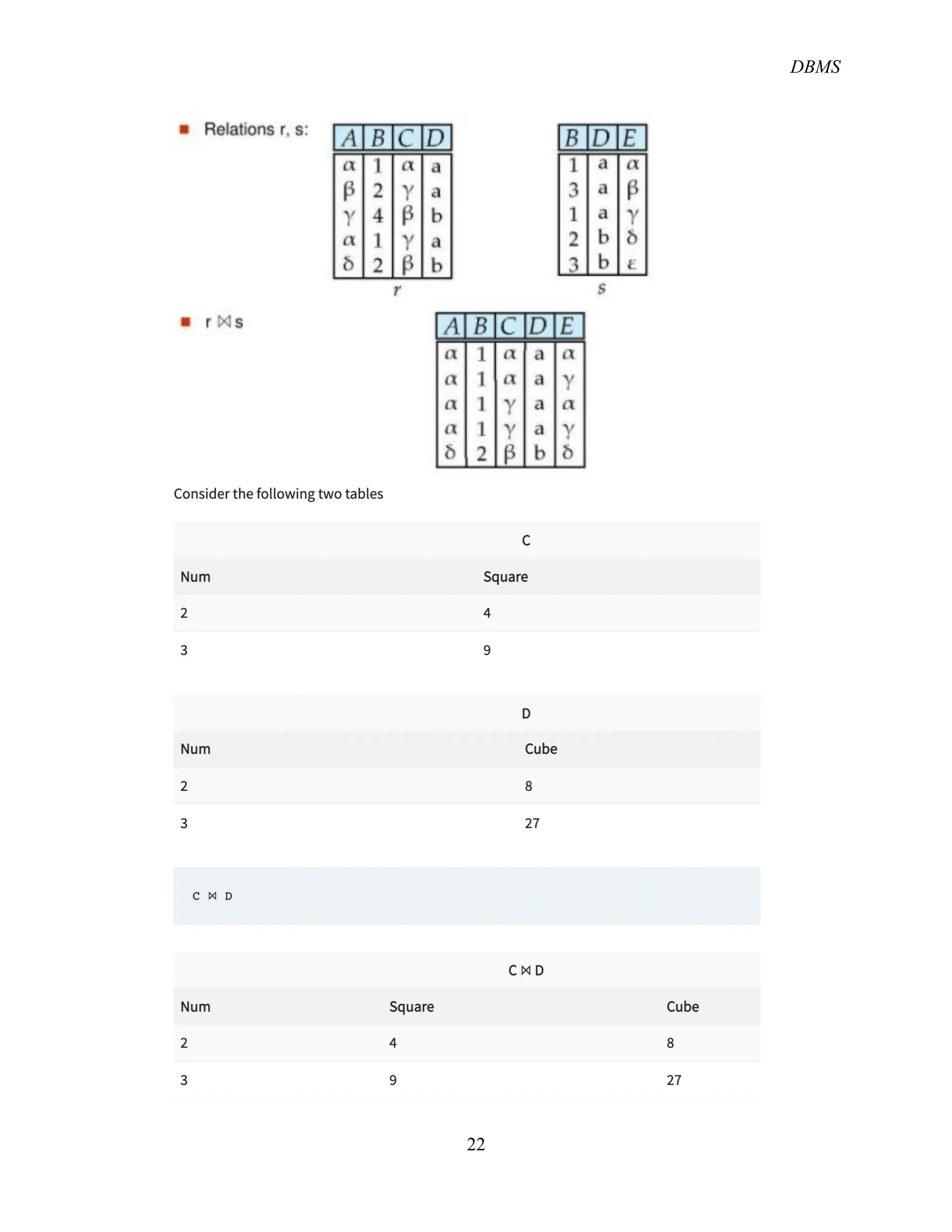
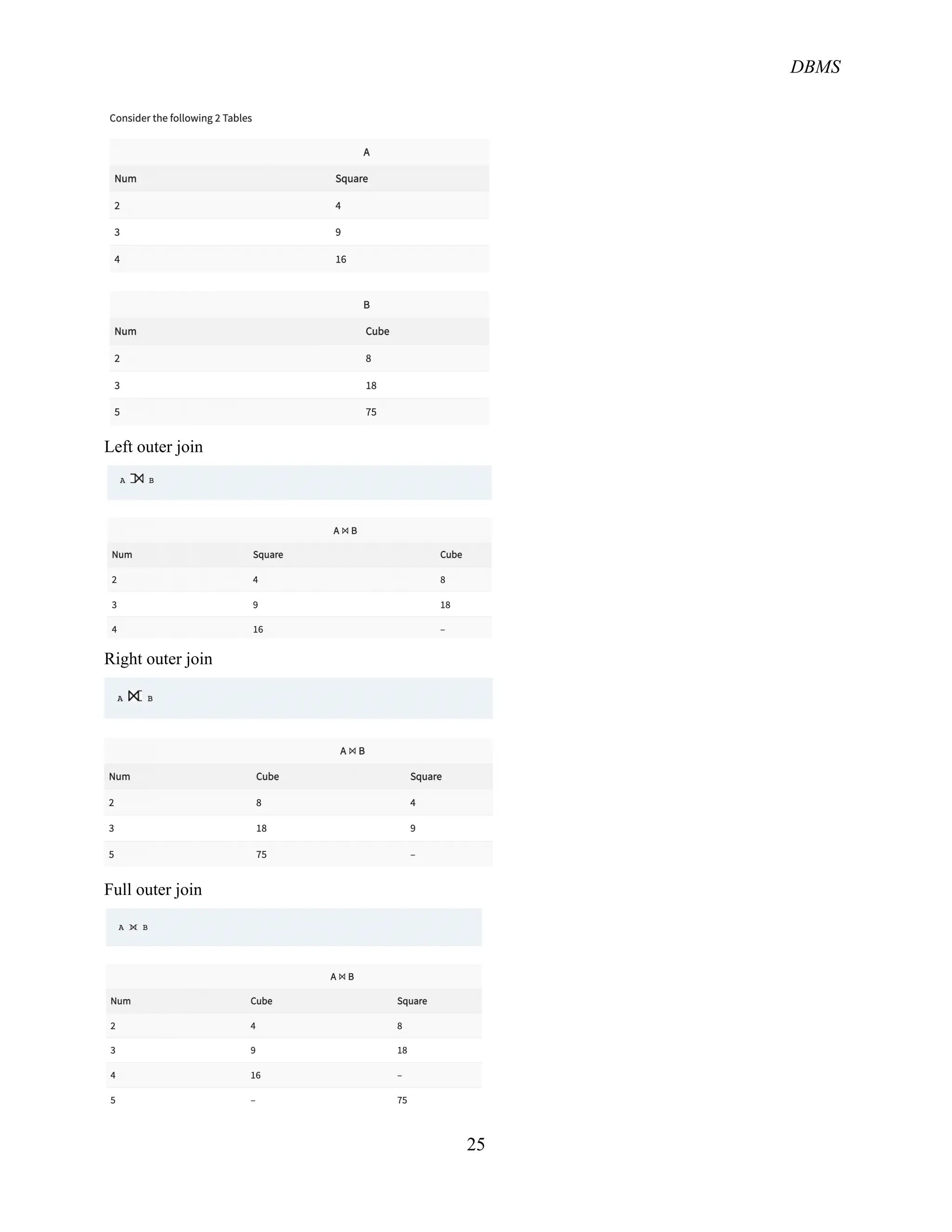
The document provides an overview of the relational database management system (RDBMS) and its structure, emphasizing its simplicity and the use of tables (relations) to represent data and relationships. It explains key concepts such as attributes, tuples, superkeys, candidate keys, primary keys, and foreign keys, along with operations in relational algebra including selection, projection, and various join types. Additionally, it outlines the schema of a university database and the role of keys in identifying records.