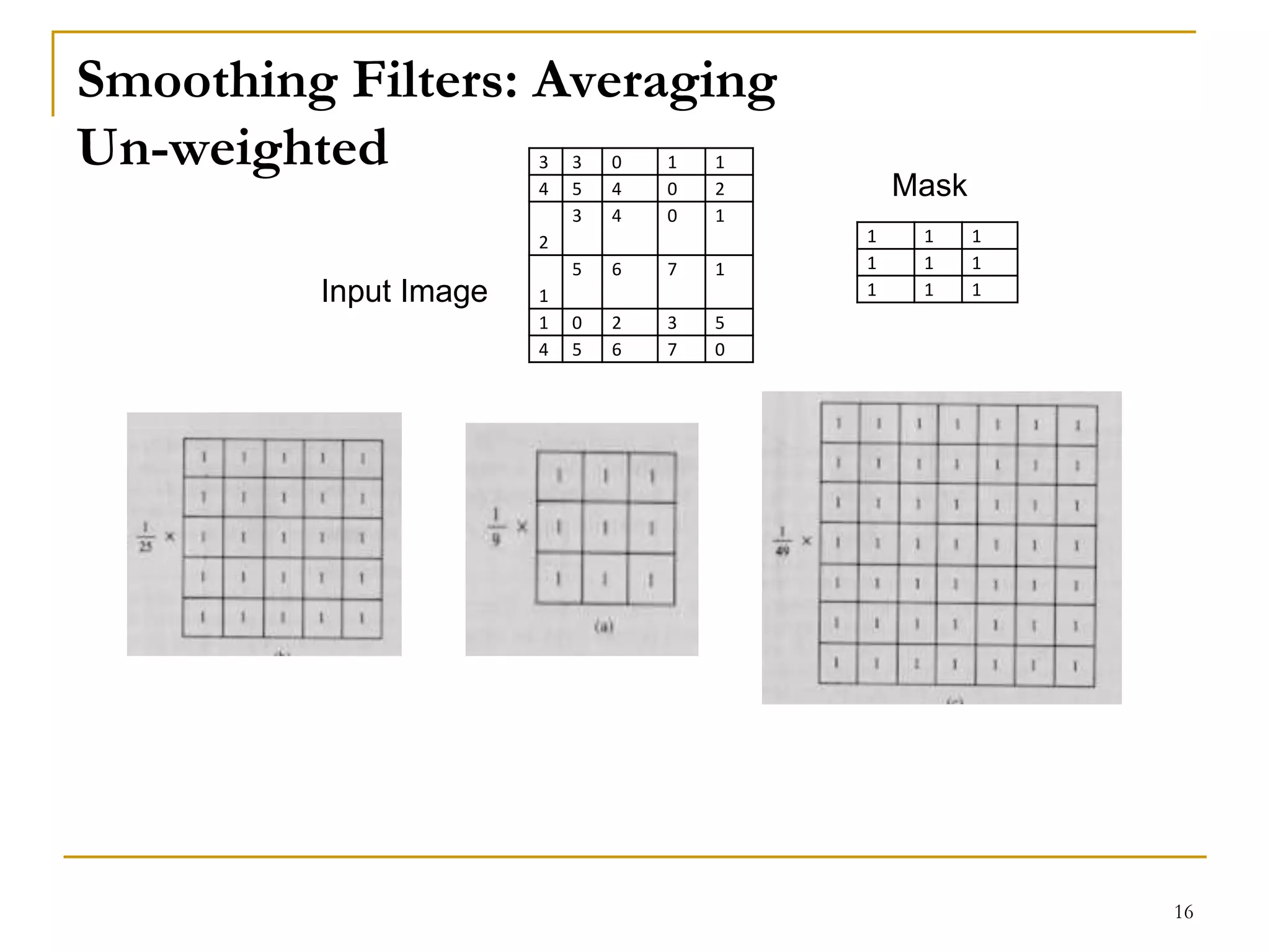
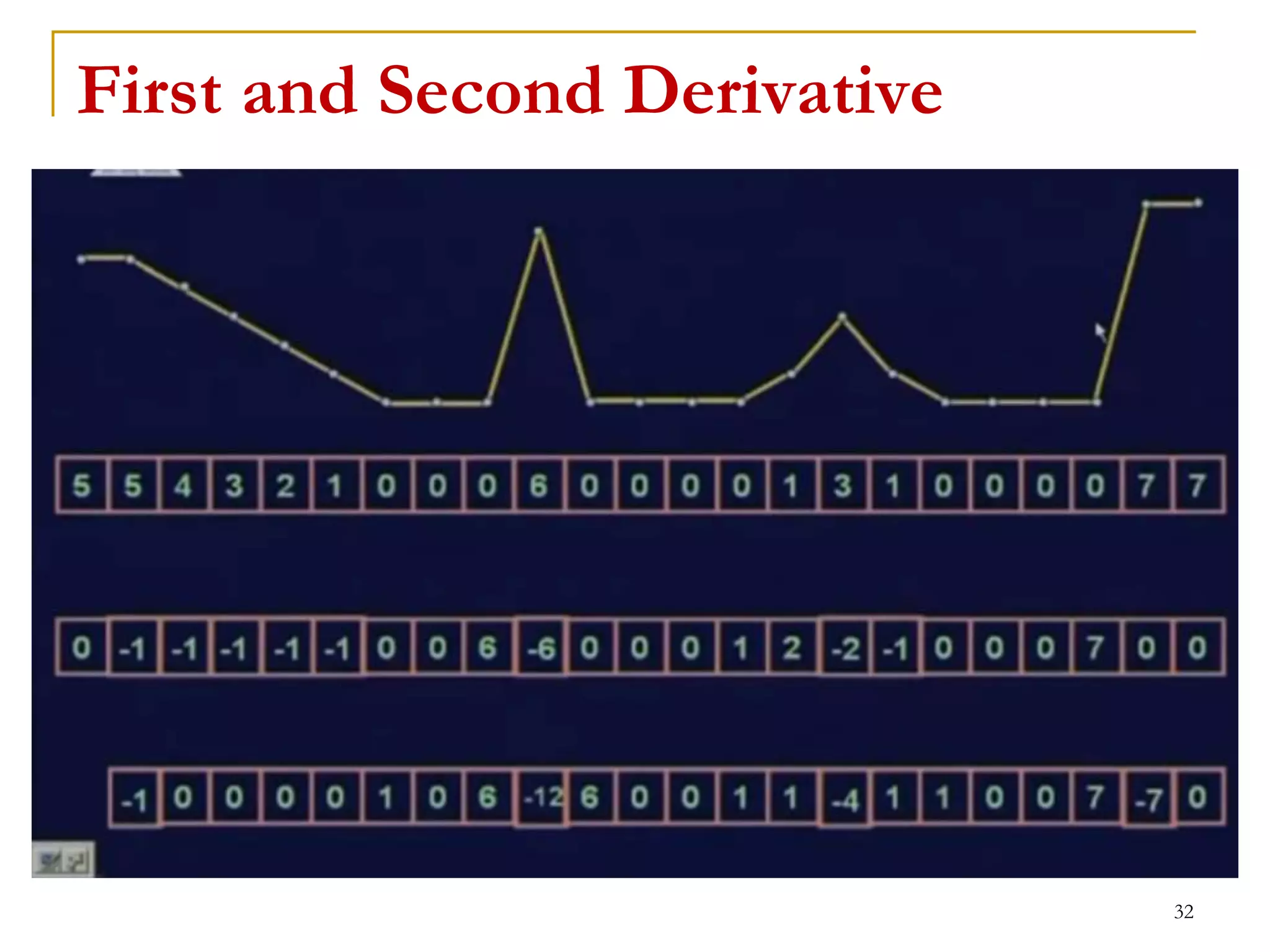
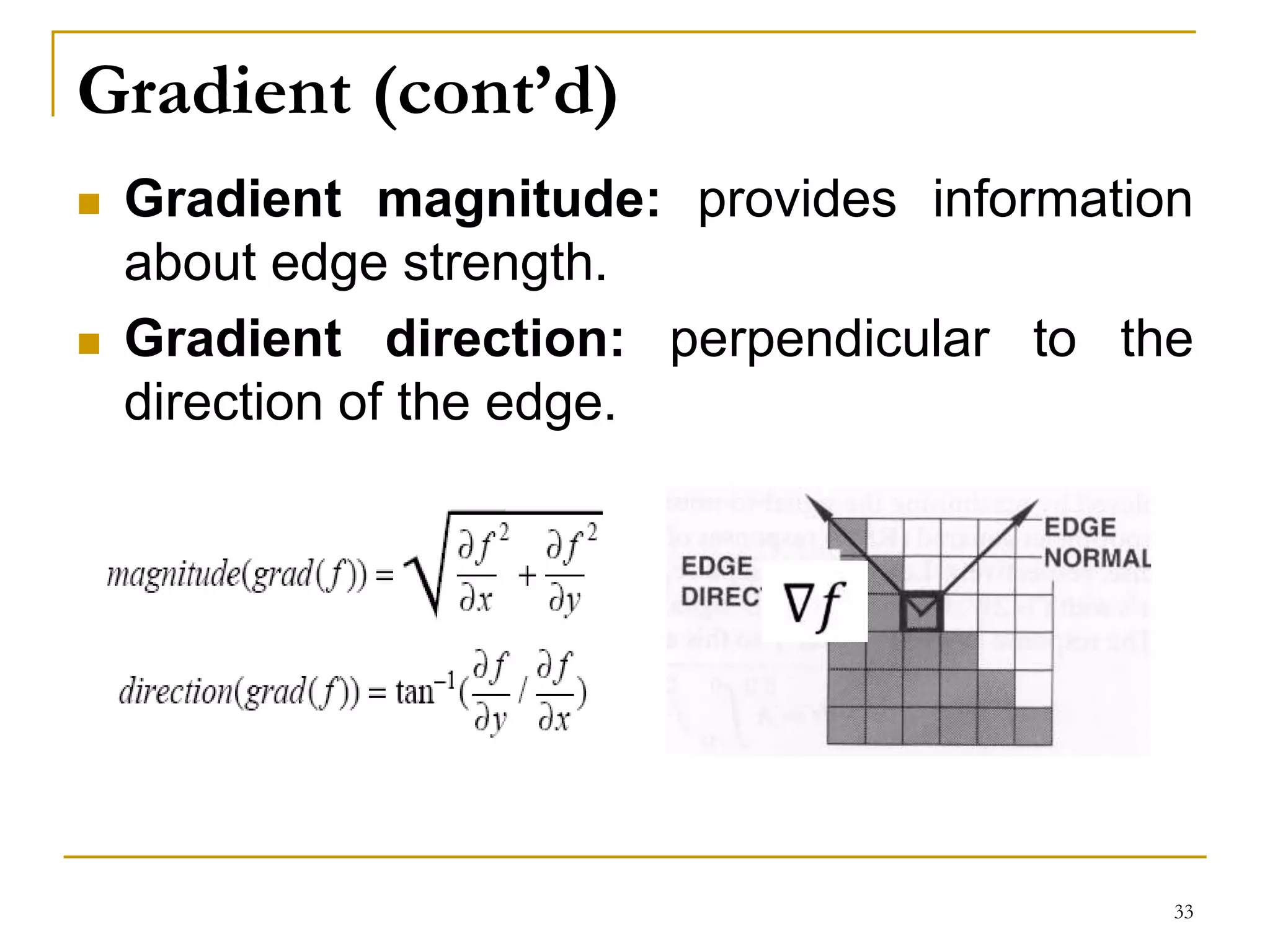
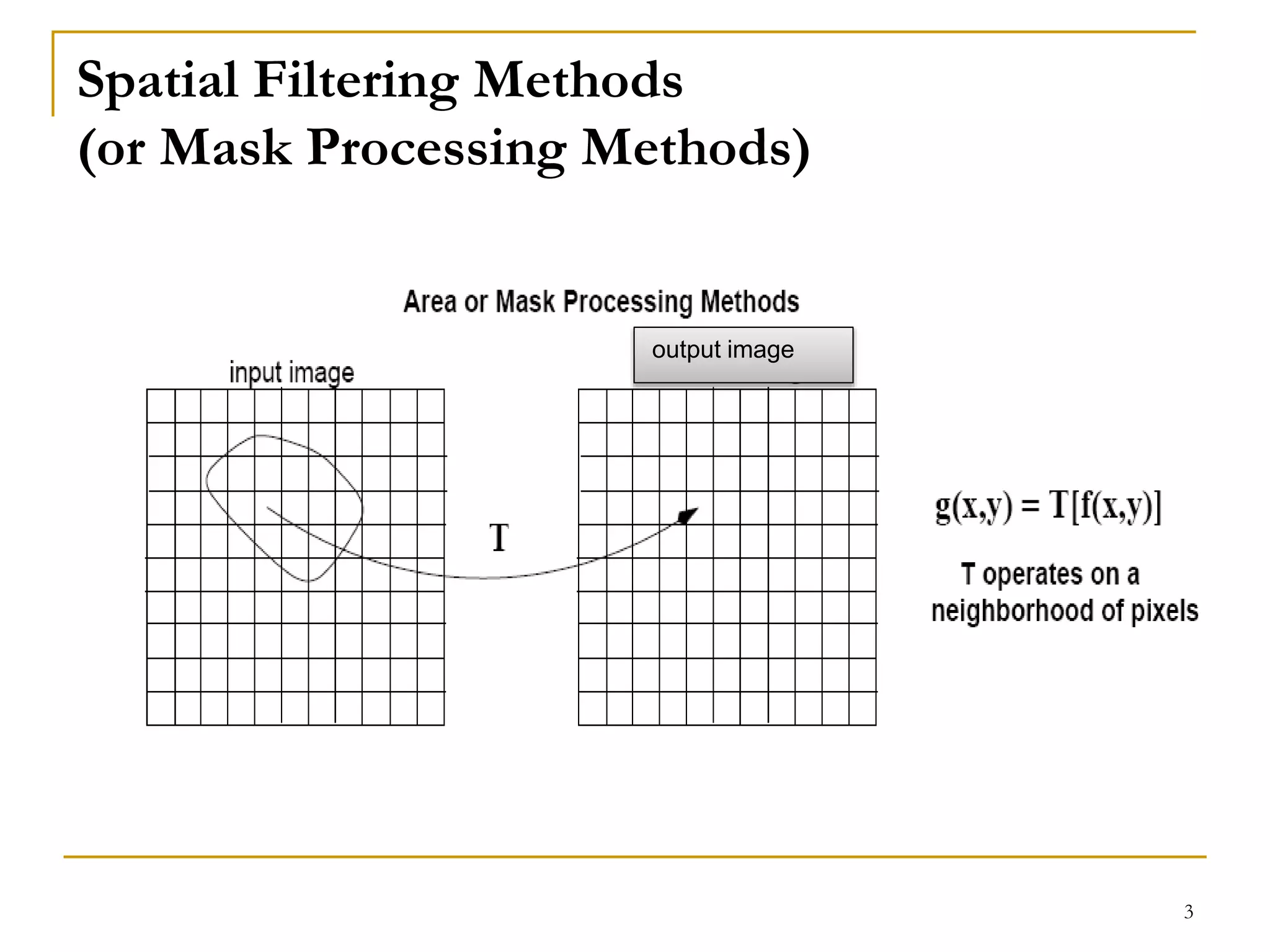
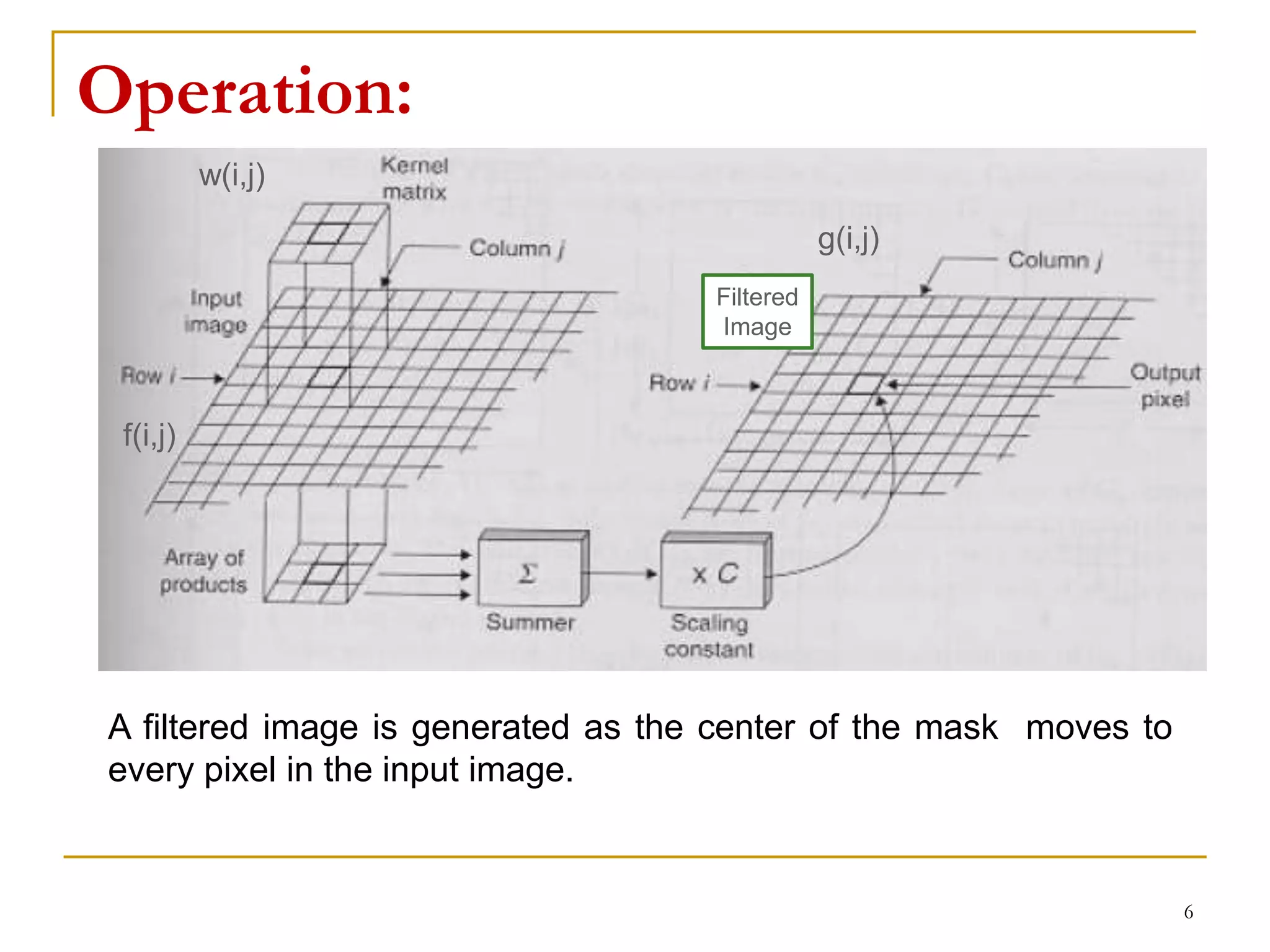
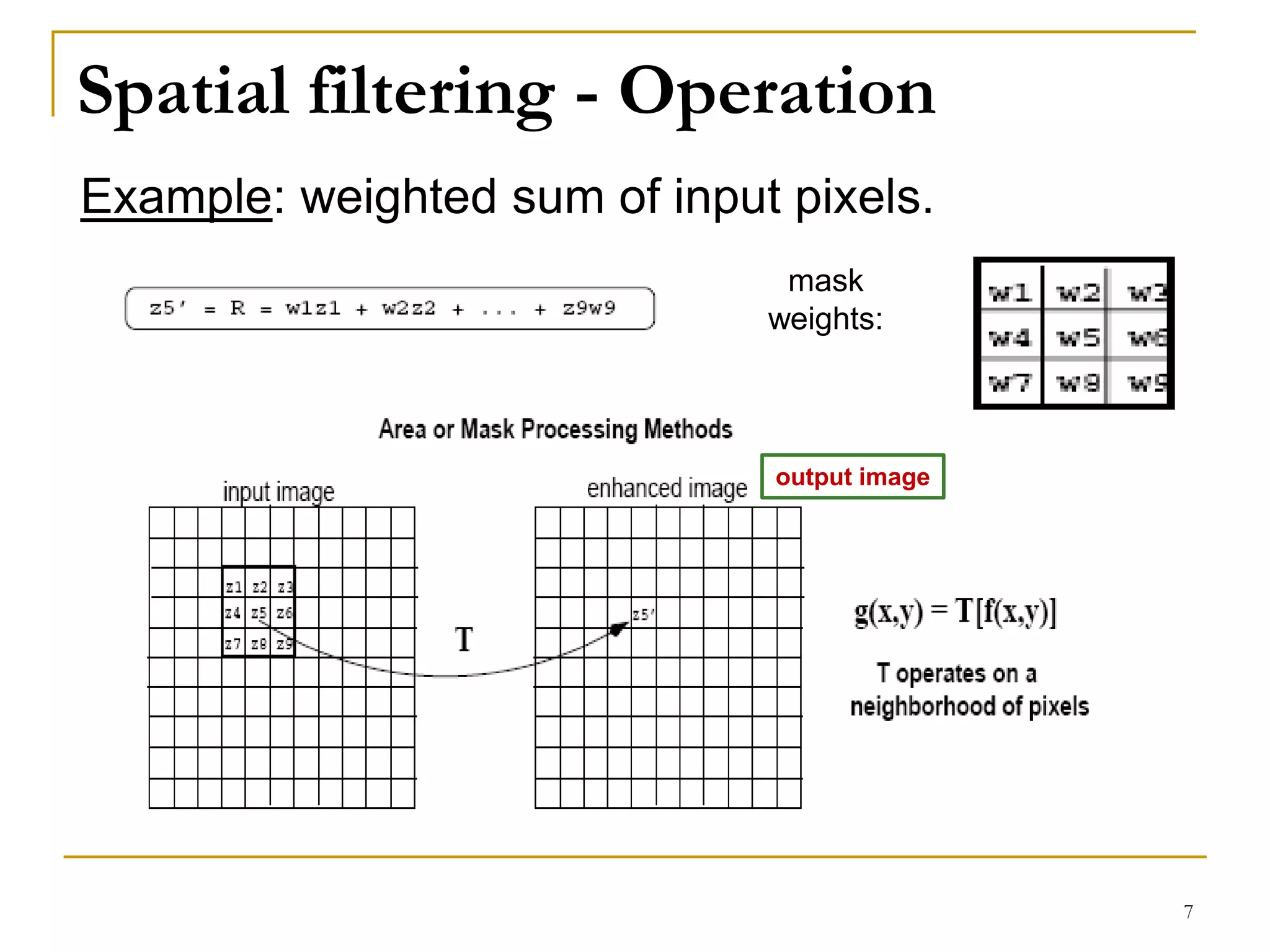
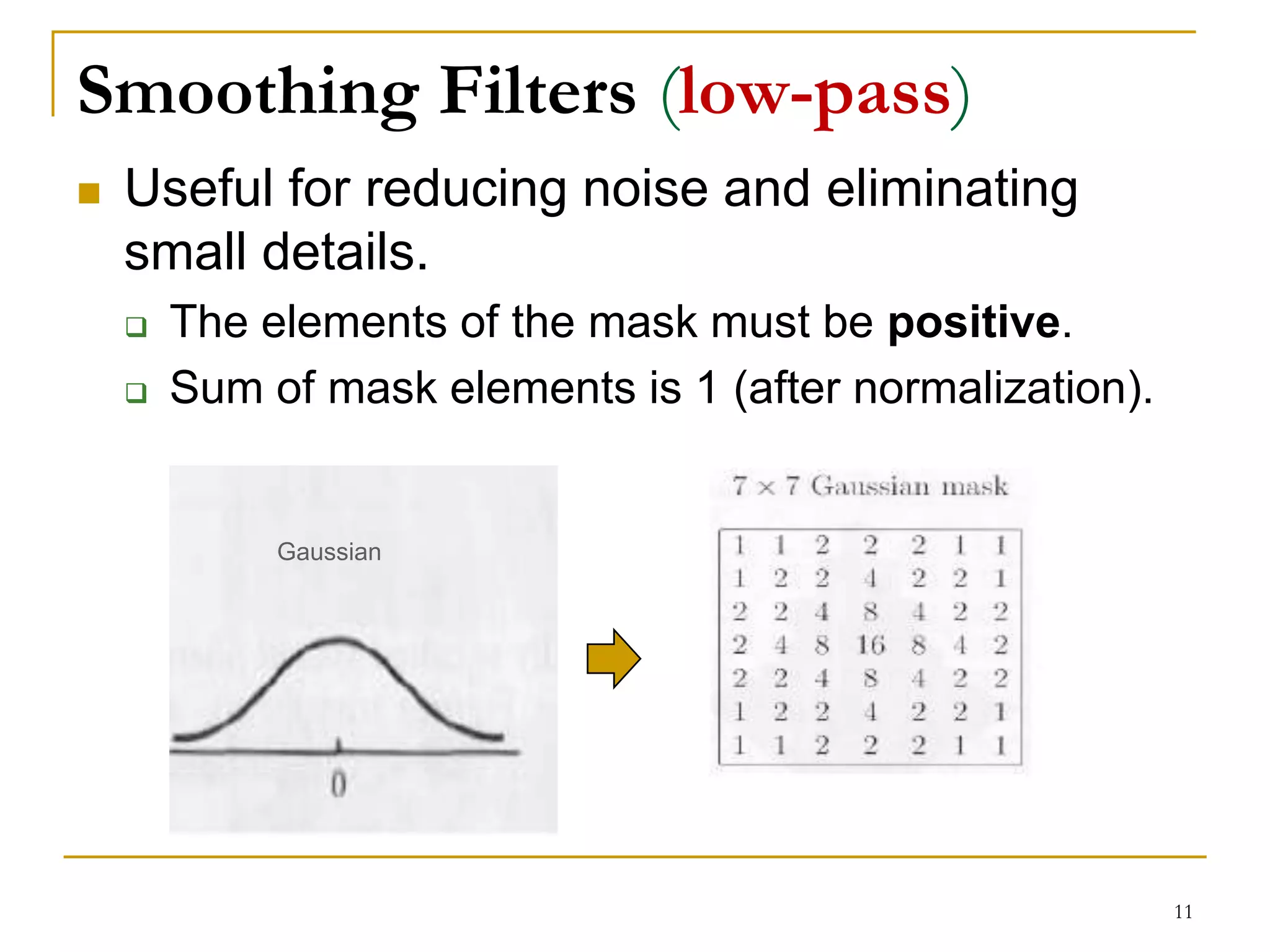
The document presents a lecture on spatial filters in image enhancement, detailing various filtering methods such as low-pass, high-pass, band-pass, and band-reject filters. It discusses the operation of spatial filtering, linear and non-linear methods, and provides examples of smoothing and sharpening filters, including their applications and effects. Additionally, it covers common filtering techniques and concludes with assignment details related to the role of digital image processing in medical imaging and computer vision.









![Sharpening Filters - Example
Warning: the results of sharpening might contain negative
values (i.e., re-map them to [0, 255])
Sharpened ImageInput Image
(for better visualization, the original
image is added to the sharpened image)
14](https://image.slidesharecdn.com/lecture13spatialfilters-181008123244/75/Spatial-Filters-Digital-Image-Processing-14-2048.jpg)