Downloaded 2,599 times
Uploaded byDeepjyoti Kalita
Turing machine by_deep
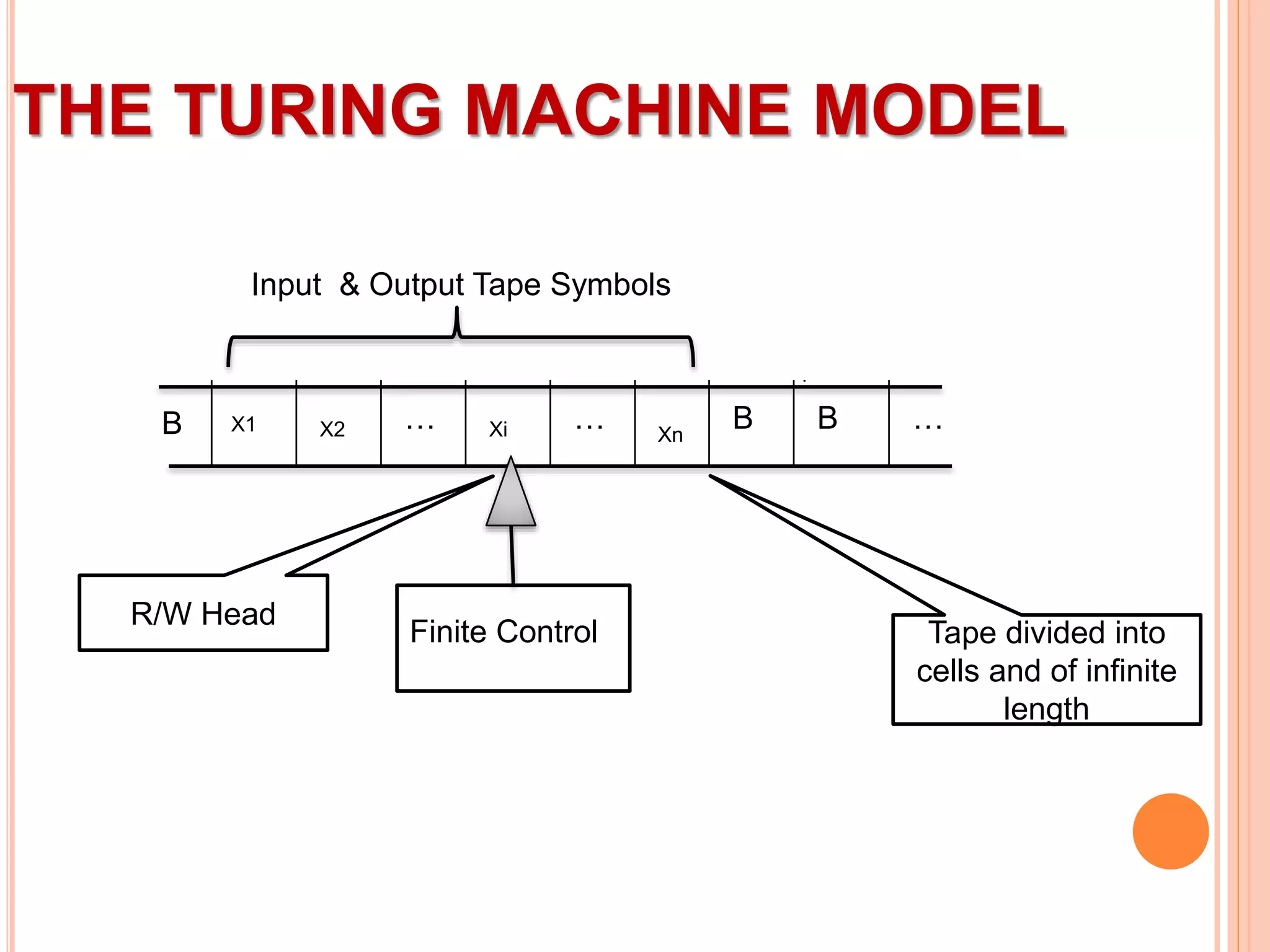
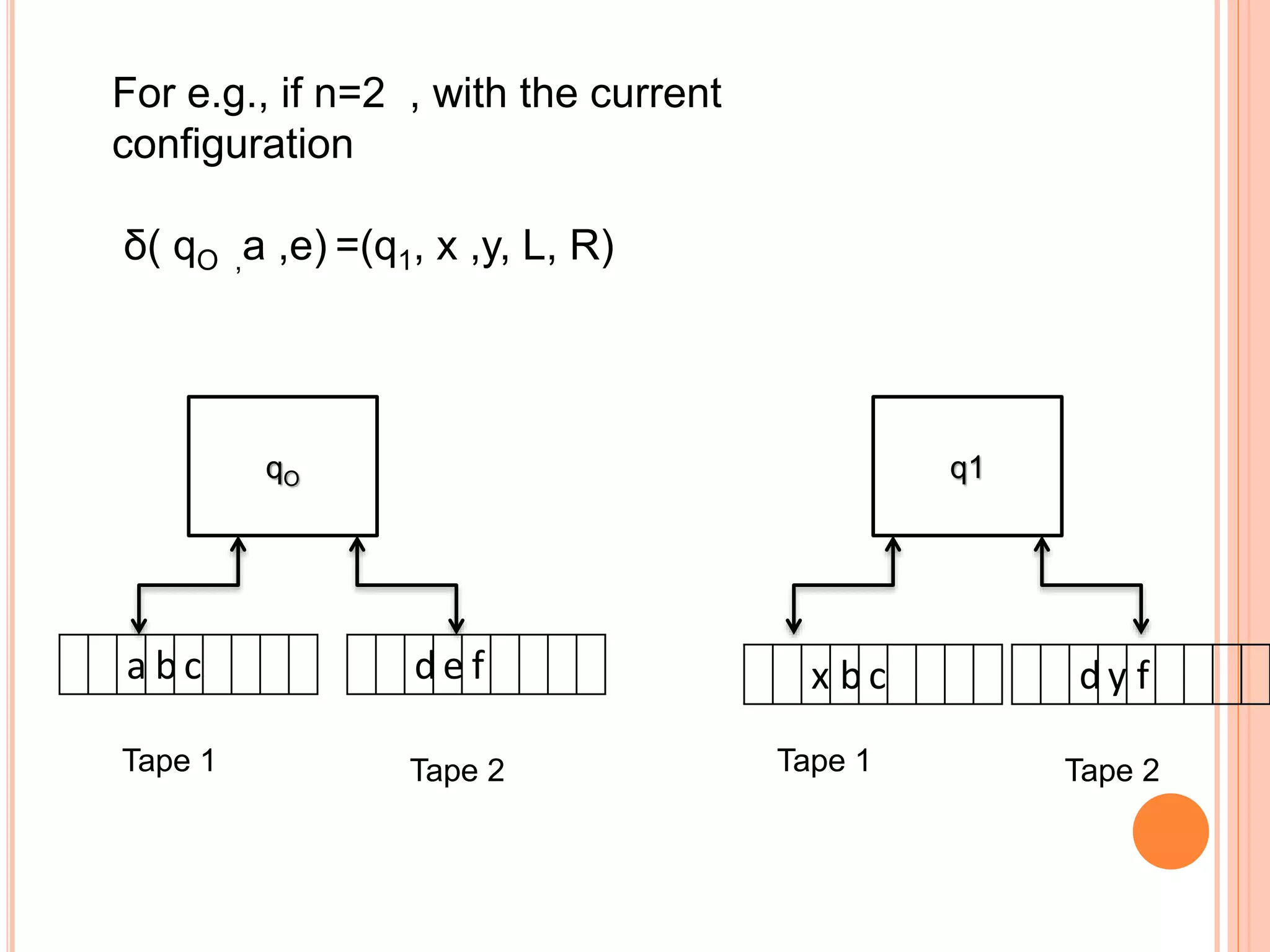
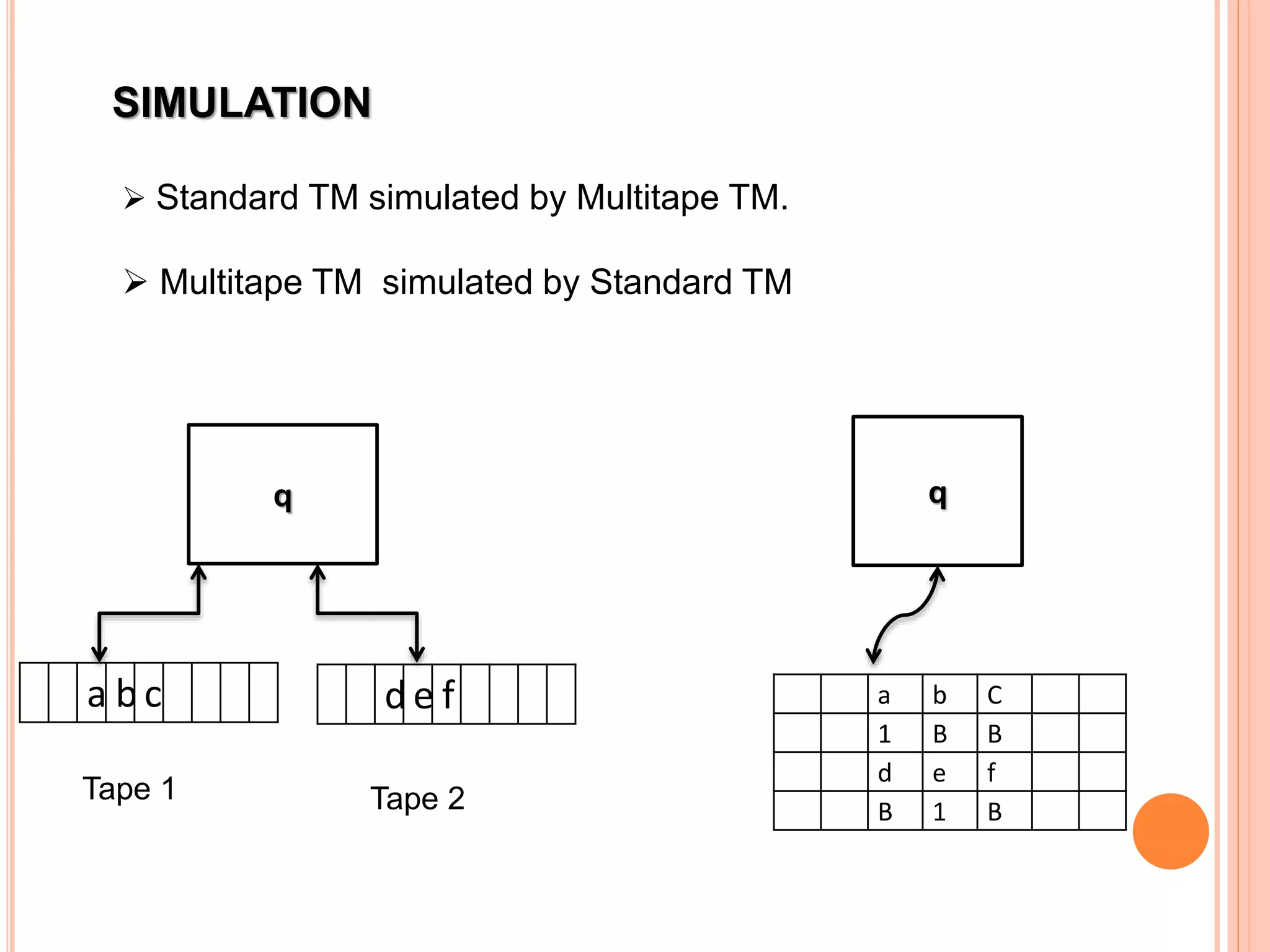
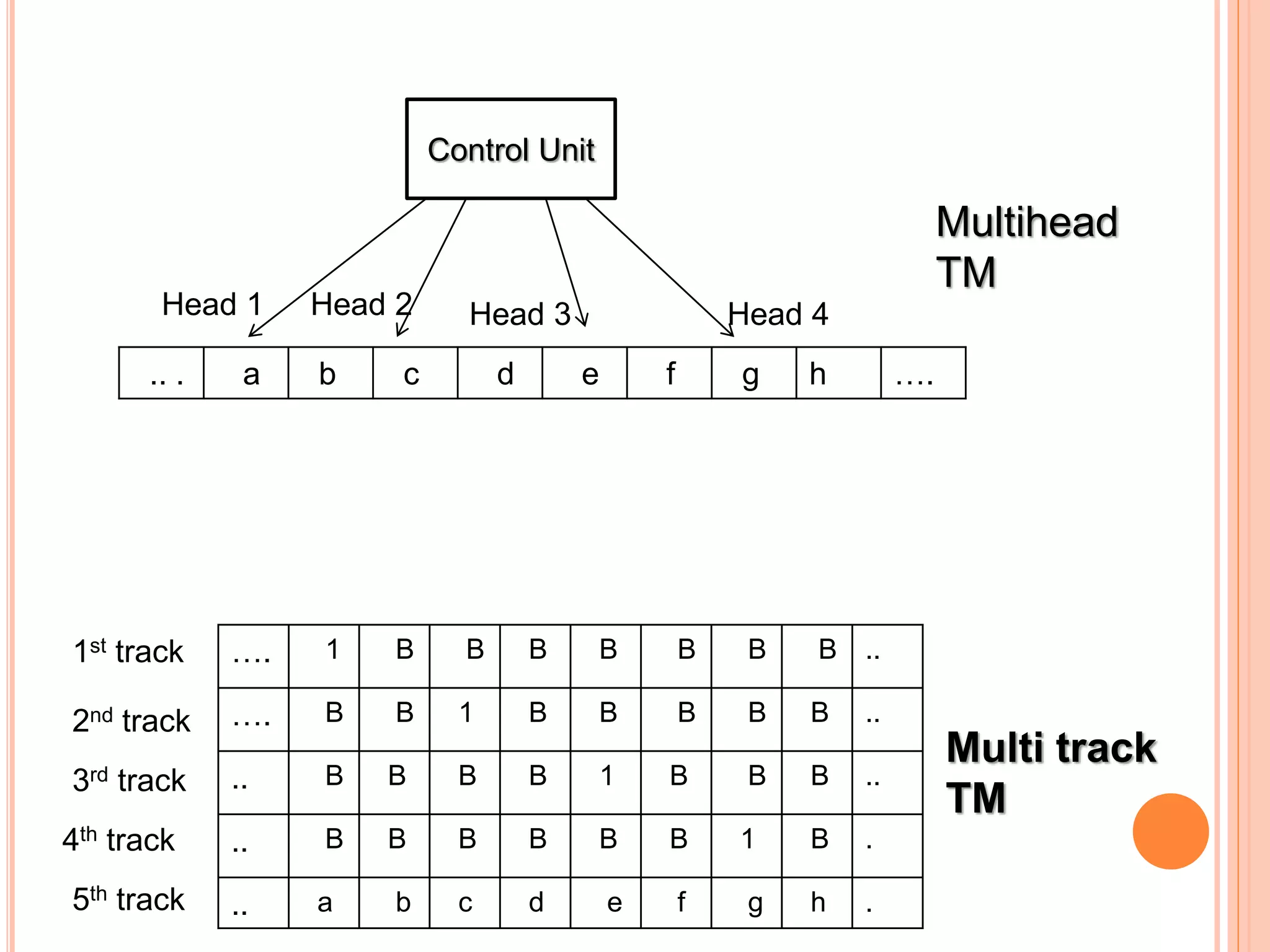
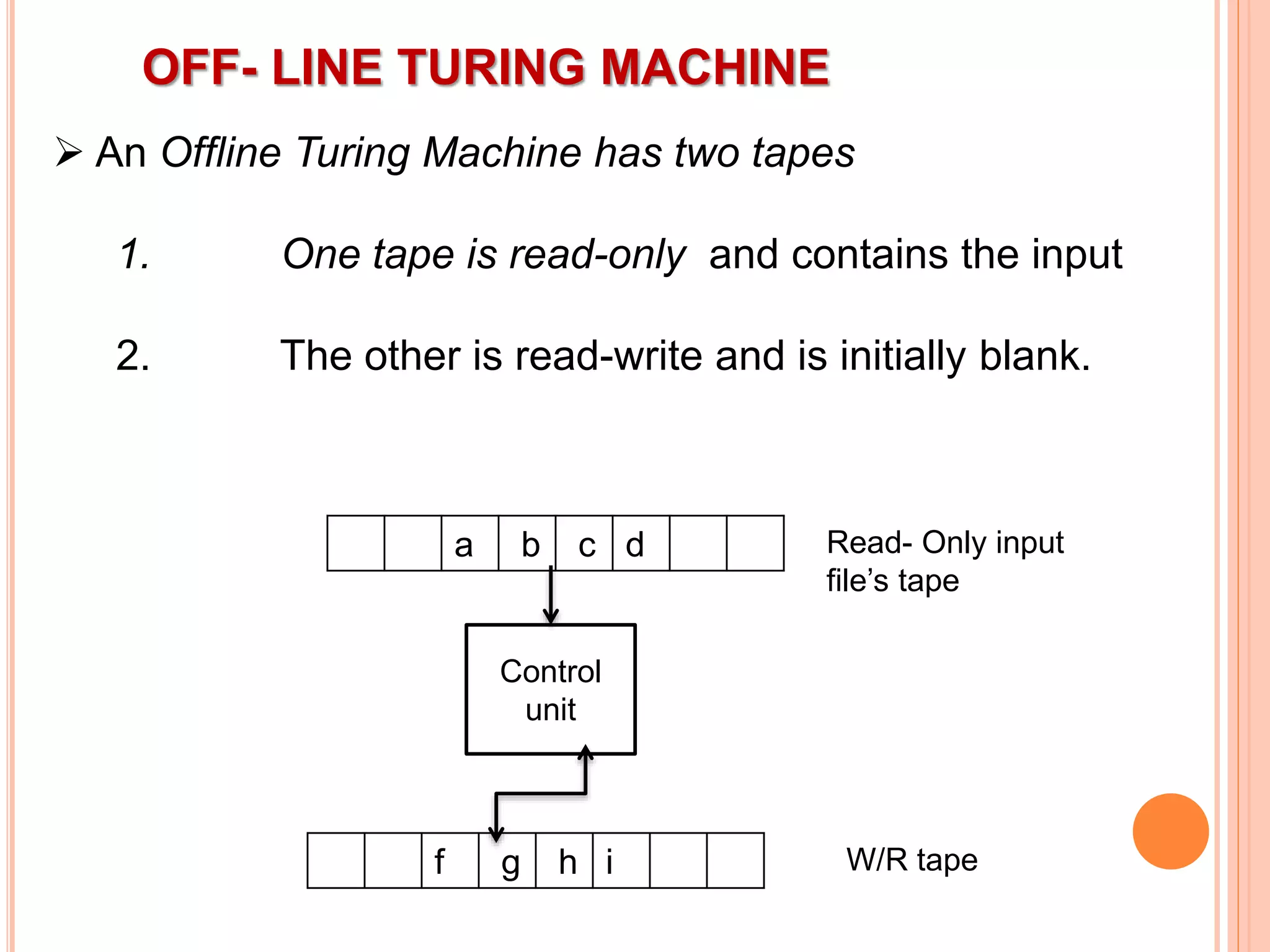
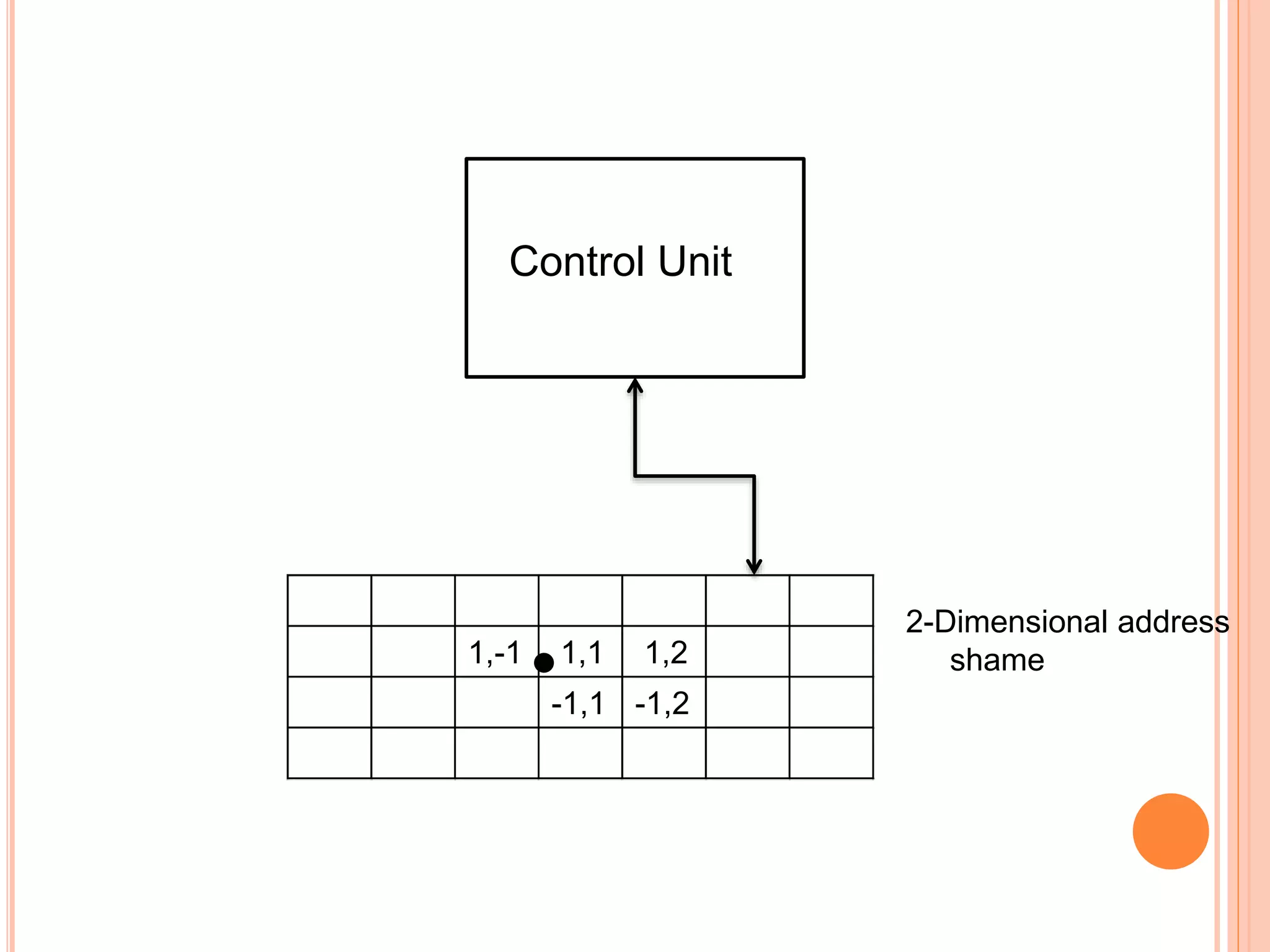
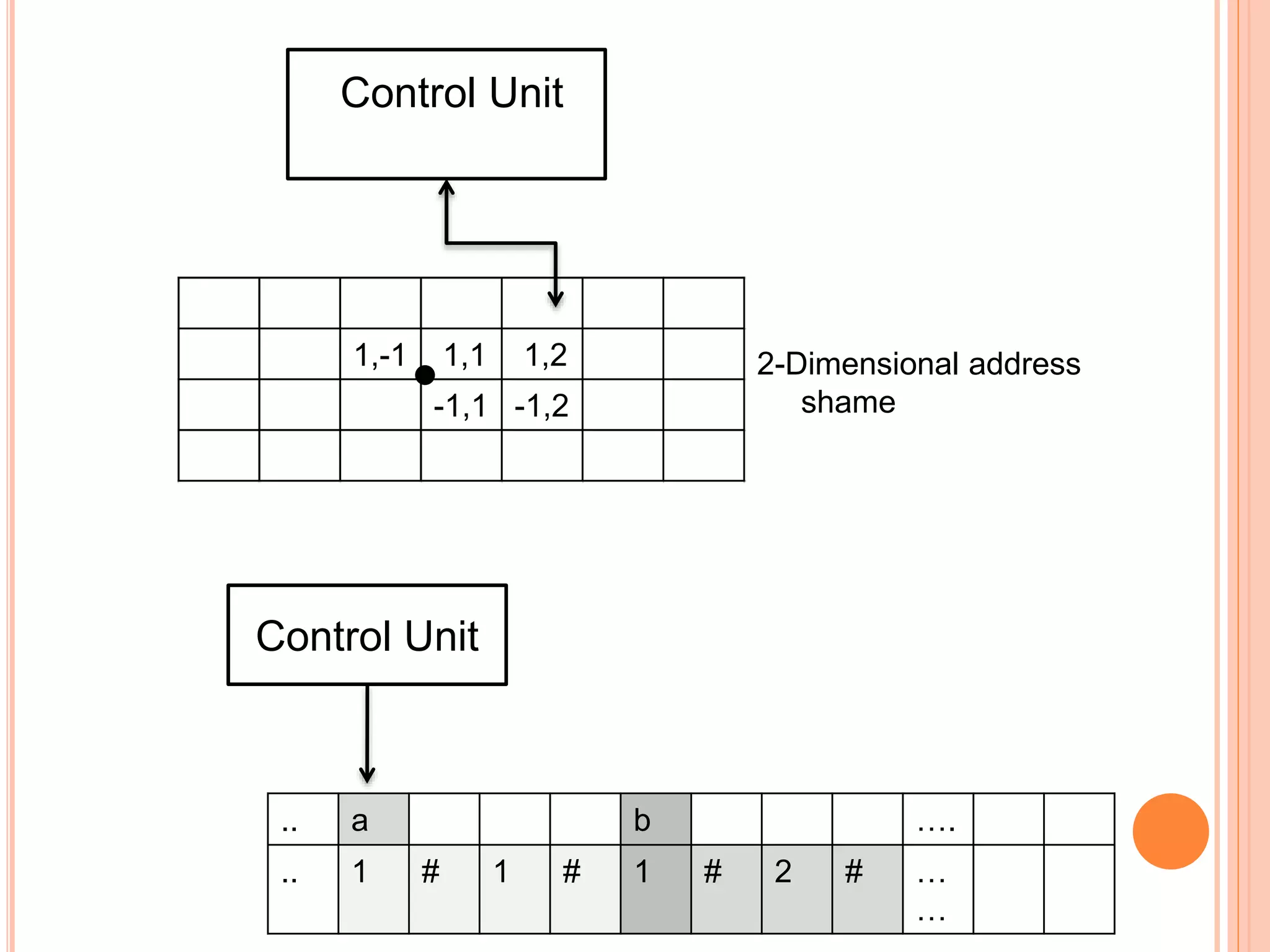
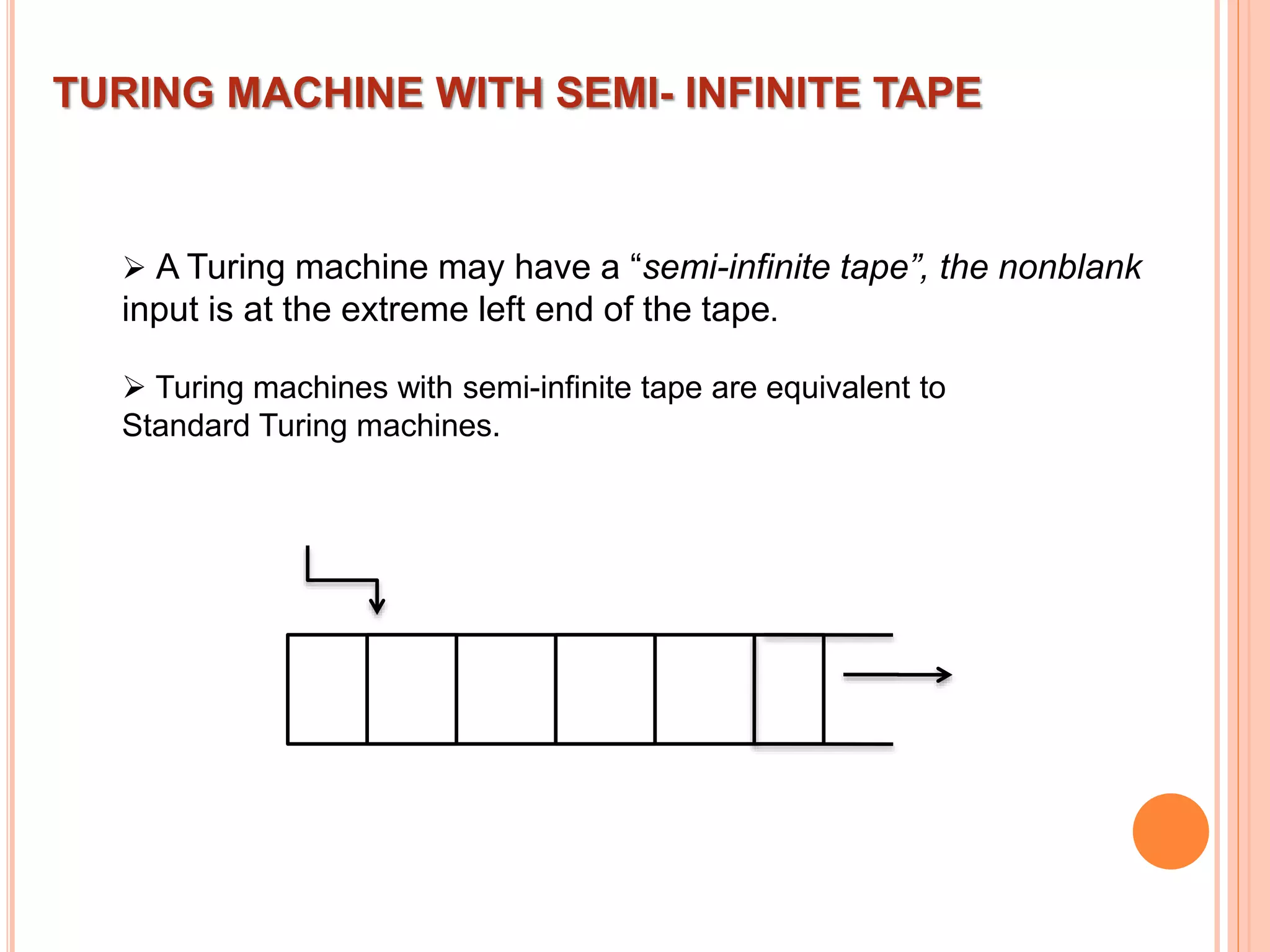
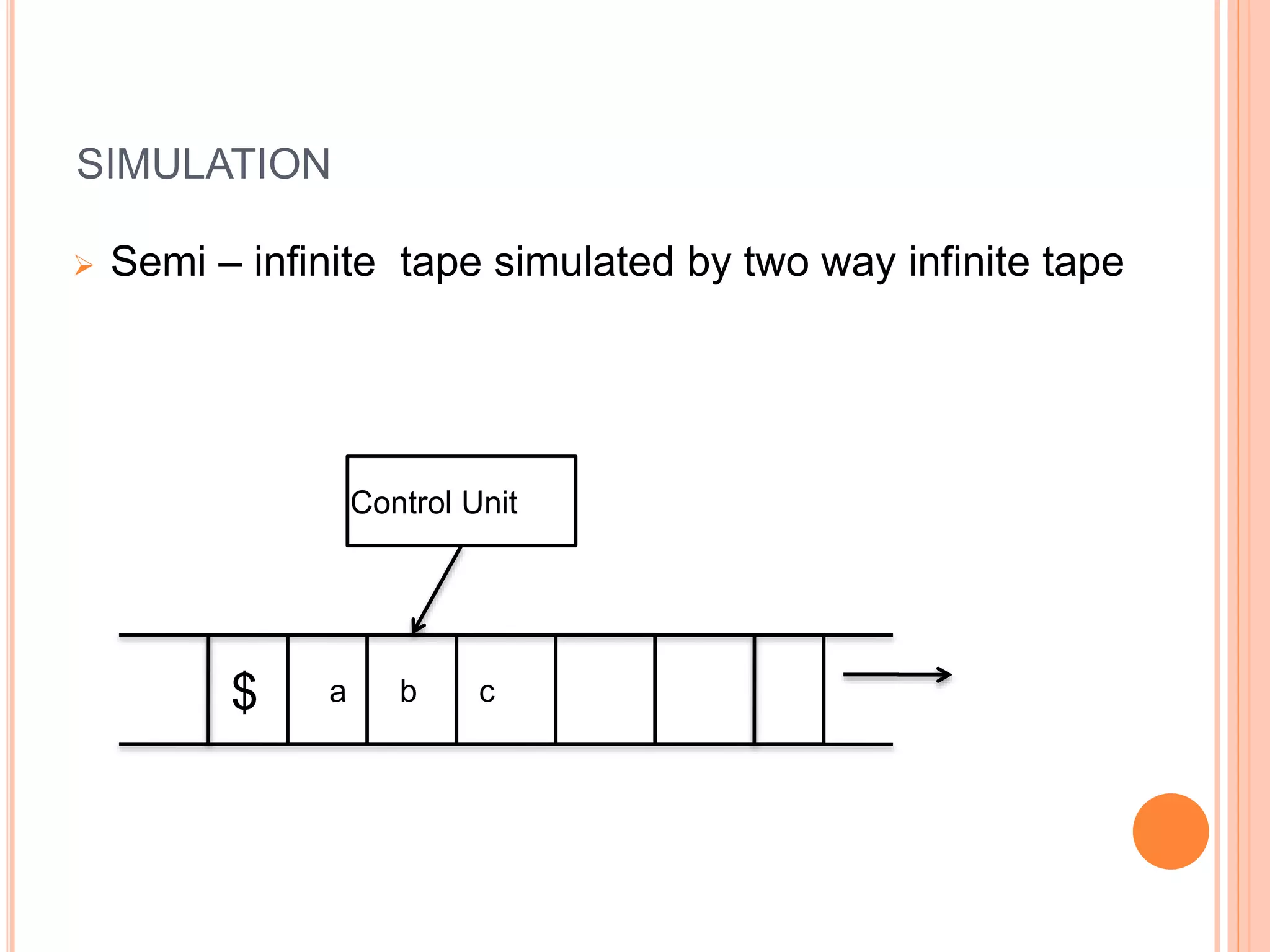
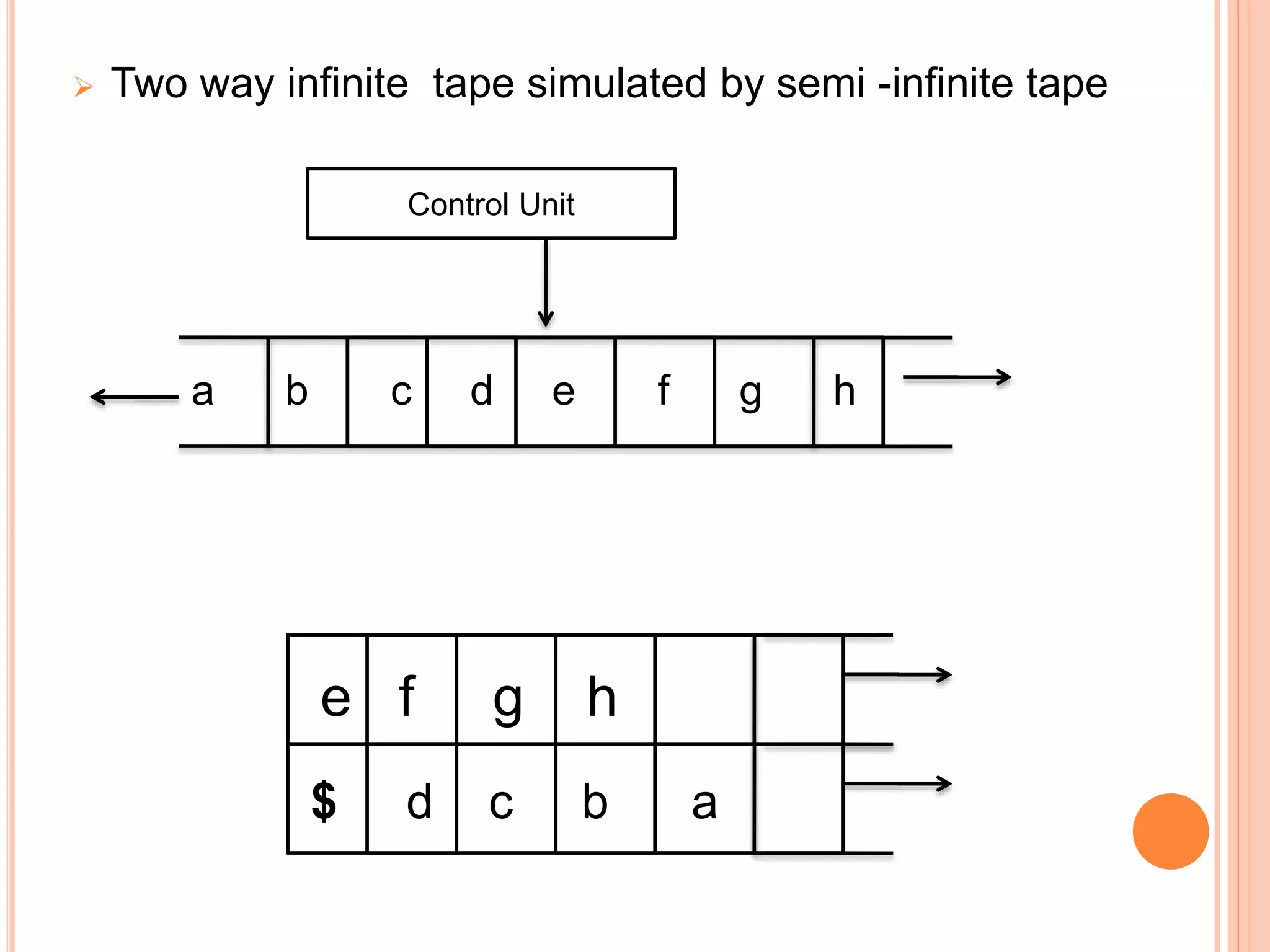
This document provides an overview of Turing machines. It introduces Turing machines as a simple mathematical model of a computer proposed by Alan Turing in 1936. A Turing machine consists of a tape divided into cells, a read/write head, finite states, and a transition function. The transition function defines how the machine moves between states and reads/writes symbols on the tape based on its current state and tape symbol. Turing machines can accept languages and compute functions. Variations include multi-tape, non-deterministic, multi-head, offline, multi-dimensional, and stationary-head Turing machines. The properties of Turing machines include their ability to recognize any language generated by a phrase-structure grammar and the Church
Turing machine by_deep
- 1. PRESENTATION ON TURING MACHINE PREPAREDBY: DEEPJYOTI KALITA CS-16 (3RD SEM) MSC COMPUTER SCIENCE GAUHATI UNIVERSITY,ASSAM Email: deepjyoti111@gmail.com
- 2. Introduced by AlanTuring in 1936. A simple mathematical model of a computer. Models the computing capability of a computer. INTRODUCING TURING MACHINES
- 3. DEFINATION A Turingmachine (TM) is a finite-state machine with an infinite tape and a tape head that can read or write one tape cell and move left or right. It normally accepts the input string, or completes its computation, by entering a final or accepting state. Tape is use for input and working storage.
- 4. Turing Machine isrepresented by- M=(Q,, Γ,δ,q0,B,F) , Where Q is the finite state of states a set of τ not including B, is the set of input symbols, τ is the finite state of allowable tape symbols, δ is the next move function, a mapping from Q × Γ to Q × Γ ×{L,R} Q0 in Q is the start state, B a symbol of Γ is the blank, F is the set of final states. Representation of Turing Machine
- 5. THE TURING MACHINEMODEL X1 X2 … Xi … Xn B B … Finite Control R/W Head B Tape divided into cells and of infinite length Input & Output Tape Symbols
- 6. TRANSITION FUNCTION Onemove (denoted by |---) in a TM does the following: δ(q , X) = (p ,Y ,R/L) q is the current state X is the current tape symbol pointed by tape head State changes from q to p
- 7. TURING MACHINE ASLANGUAGE ACCEPTORS A Turing machine halts when it no longer has available moves. If it halts in a final state, it accepts its input, otherwise it rejects its input. For language accepted by M ,we define L(M)={ w ε ∑+ : q0w |– x1qfx2 for some qf ε F , x1 ,x2ε Γ *}
- 8. TURING MACHINE ASTRANSDUCERS To use a Turing machine as a transducer, treat the entire nonblank portion of the initial tape as input Treat the entire nonblank portion of the tape when the machine halts as output. A Turing machine defines a function y = f (x) for strings x, y ε ∑* if q0x |*– qf y A function index is “Turing computable” if there exists a Turing machine that can perform the above task.
- 9. ID OF ATM Instantaneous Description or ID : X1 X2…Xi-1 q Xi Xi+1 …Xn Means: q is the current state Tape head is pointing to Xi X1X2…Xi-1XiXi+1… Xn are the current tape symbols δ (q , Xi ) = (p ,Y , R ) is same as: X1 X2…Xi-1 q Xi Xi+1 …Xn |---- X1 X2…Xi-1 Y p Xi+1…Xn δ (q Xi) = (p Y L) same as: X1 X2…Xi-1 q Xi Xi+1 …Xn |---- X1 X2…pXi-1Y Xi+1 …Xn
- 10. TECHNIQUES FOR TMCONSTRUCTION Storage in the finite control Using multiple tracks Using Check off symbols Shifting over Implementing Subroutine
- 11. VARIATIONS OF TURINGMACHINES Multitape Turing Machines Non deterministic Turing machines Multihead Turing Machines Off-line Turing machines Multidimensional Turing machines
- 12. MULTITAPE TURING MACHINES A Turing Machine with several tapes Every Tape’s have their Controlled own R/W Head For N- tape TM M=(Q,, Γ,δ,q0,B,F) we define δ : Q X ΓN Q X ΓN X { L , R} N
- 13. For e.g., ifn=2 , with the current configuration δ( qO ,a ,e) =(q1, x ,y, L, R) qO a b c d e f Tape 1 Tape 2 q1 d y f Tape 1 Tape 2 x b c
- 14. SIMULATION Standard TMsimulated by Multitape TM. Multitape TM simulated by Standard TM q a b c d e f Tape 1 Tape 2 a b C 1 B B d e f B 1 B q
- 15. NON DETERMINISTIC TURINGMACHINES It is similar to DTM except that for any input symbol and current state it has a number of choices A string is accepted by a NDTM if there is a sequence of moves that leads to a final state The transaction function δ : Q X Γ 2 Q X Γ X { L , R}
- 16. Simulation: A DTMsimulated by NDTM In straight forward way . A NDTM simulated by DTM A NDTM can be seen as one that has the ability to replicate whenever is necessary
- 17. MULTIHEAD TURING MACHINE Multihead TM has a number of heads instead of one. Each head indepently read/ write symbols and move left / right or keep stationery. a b c d e f g t Control unit
- 18. SIMULATION Standard TMsimulated by Multihead TM. - Making on head active and ignore remaining head Multihead TM simulated by standard TM. - For k heads Using (k+1) tracks if there is..
- 19. .. . ab c d e f g h …. Control Unit …. 1 B B B B B B B .. …. B B 1 B B B B B .. .. B B B B 1 B B B .. .. B B B B B B 1 B . .. a b c d e f g h . Head 1 Head 2 Head 3 Head 4 Multihead TM Multi track TM 1st track 2nd track 3rd track 4th track 5th track
- 20. OFF- LINE TURINGMACHINE An Offline Turing Machine has two tapes 1. One tape is read-only and contains the input 2. The other is read-write and is initially blank. a b c d Control unit f g h i Read- Only input file’s tape W/R tape
- 21. SIMULATION A StandardTM simulated by Off-line TM An Off- line TM simulated by Standard TM a b c d B B 1 B f g h i B 1 B B Control Unit M’ a b c d Control Unit M f g h i Read- Only input W/R tape
- 22. MULTIDIMENSIONAL TURING MACHINE AMultidimensional TM has a multidimensional tape. For example, a two-dimensional Turing machine would read and write on an infinite plane divided into squares, like a checkerboard. For a two- Dimensional Turing Machine transaction function define as: δ : Q X Γ Q X Γ X { L , R,U,D}
- 23. 1,-1 1,1 1,2 -1,1-1,2 Control Unit 2-Dimensional address shame
- 24. SIMULATION Standard TMsimulated by Multidimensional TM Multidimensional TM simulated by Standard TM.
- 25. 1,-1 1,1 1,2 -1,1-1,2 Control Unit 2-Dimensional address shame .. a b …. .. 1 # 1 # 1 # 2 # … … Control Unit
- 26. TURING MACHINE WITHSEMI- INFINITE TAPE A Turing machine may have a “semi-infinite tape”, the nonblank input is at the extreme left end of the tape. Turing machines with semi-infinite tape are equivalent to Standard Turing machines.
- 27. SIMULATION Semi –infinite tape simulated by two way infinite tape $ a b c Control Unit
- 28. Two wayinfinite tape simulated by semi -infinite tape a b c d e f g h $ d c b a e f g h Control Unit
- 29. TURING MACHINE WITHSTATIONARY HEAD Here TM head has one another choice of movement is stay option , S. we define new transaction function, δ : Q X Γ Q X Γ X { L , R, S}
- 30. SIMULATION TM withstay option can simulate a TM without stay option by not using the stay option. TM with stay option can simulate by a TM without stay option by not using the stay option. In TM with stay option: δ(q, X)= ( p , Y, S ) In TM without stay option : δ’(q, X)= ( qr , Y, R ) δ’( qr, A)= ( p , A, L ) ¥ AεΓ’
- 31. RECURSIVE AND RECURSIVELYENUMERABLE LANGUAGE The Turing machine may 1. Halt and accept the input 2. Halt and reject the input, or 3. Never halt /loop. Recursively Enumerable Language: There is a TM for a language which accept every string otherwise not.. Recursive Language: There is a TM for a language which halt on every string.
- 32. UNIVERSAL LANGUAGE ANDTURING MACHINE The universal language Lu is the set of binary strings that encode a pair (M , w) where w is accepted by M A Universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input.
- 33. PROPERTIES OF TURINGMACHINES A Turing machine can recognize a language iff it can be generated by a phrase-structure grammar. The Church-Turing Thesis: A function can be computed by an algorithm iff it can be computed by a Turing machine.
- 34.