Y - Recursion The Hard Way GopherCon EU 2025

RECURSION THE HARD WAY
Y
ELEANOR MCHUGH
@feyeleanor

Days of The Underground
Walk on the Wild Side
The Filthy Lucre Tour

DISCLAIMER
experimental code and concepts ahead
if it doesn't look idiomatic... it probably isn't
all examples are for entertainment purposes only
and may appear simpler than they really are
tested exclusively on Intel MacBooks with go 1.24.4
do not do any of this on main!
any resemblance to actual code & conceptstm - living or dead - is intentional
github://feyeleanor/y_recursion_the_hard_way

FUNCTIONAL PROGRAMMING
A DIFFERENT WAY OF CODING

ADD() IS A PURE FUNCTION - IT HAS NO SIDE EFFECTS
package main
import "os"
func main() {
os.Exit(add(3, 4))
}
func add(x int, y int) int {
return x + y
}
01.GO

GENERICS AND PURE FUNCTIONS MAKE A GREAT MATCH
type Integer interface {
~int | ~int8 | ~int16 | ~int32 | ~int64 |
~uint | ~uint8 | ~uint16 | ~uint32 | ~uint64
}
type Scalar interface {
Integer | ~float32 | ~float64
}
func main() {
os.Exit(add(3, 4))
}
func add[T Scalar](x, y T) T {
return x + y
}
02.GO

GLOBAL VARIABLES INTRODUCE SIDE-EFFECTS
func main() {
for i, v := range os.Args[1:] {
x, _ := strconv.Atoi(v)
if i / 2 == 0 {
sum += x
} else {
accumulate(x)
}
}
os.Exit(sum)
}
var sum int
func accumulate(x int) {
sum += x
}
04.GO

AN IMPURE FUNCTION HAS SIDE-EFFECTS
func main() {
for _, v := range os.Args[1:] {
accumulate(x)
}
os.Exit(accumulate(0))
}
var sum int
func accumulate(x int) int {
sum += x
return sum
}
05.GO

OBJECT METHODS CAN ALSO HAVE SIDE-EFFECTS
func main() {
a.Add(x)
}
os.Exit(int(a))
}
var a Accumulator
type Accumulator int
func (a *Accumulator) Add(x int) {
*a += Accumulator(x)
}
06.GO

FUNCTION CLOSURES ALLOW PRIVATE SIDE-EFFECTS
func main() {
a := MakeAccumulator()
a(x)
}
os.Exit(a(0))
}
type Accumulator func(int) int
func MakeAccumulator() Accumulator {
var sum int
return func(x int) int {
sum += x
return sum
}
}
07.GO

A FUNCTION WITH PRIVATE SIDE-EFFECTS CAN ALSO BE AN OBJECT
func main() {
a := MakeAccumulator[int]()
a(x)
}
os.Exit(a.Int())
}
type Accumulator[T Scalar] func(T) T
func MakeAccumulator[T Scalar]() Accumulator[T] {
var sum T
return func(x T) T {
sum += x
return sum
}
}
func (a Accumulator[T]) Int() int {
return int(a(0))
}
08.GO

A FUNCTION WITH PRIVATE SIDE-EFFECTS CAN ALSO BE AN OBJECT
func main() {
var n []int
n = append(n, x)
}
os.Exit(MakeAccumulator(n...).Int())
}
func MakeAccumulator[T Scalar](s ...T) (a Accumulator[T]) {
var sum T
a = func(x T) T {
sum += x
return sum
}
for _, v := range s {
a.Add(v)
}
return
}
func (a Accumulator[T]) Add(x any) Accumulator[T] {
switch x := x.(type) {
case T:
a(x)
case Accumulator[T]:
a(x(0))
}
return a
}
09.GO

OBJECTS CAN BE DEFINED BY CONCRETE OR STRUCTURAL TYPE
func main() {
var n []int
n = append(n, x)
}
os.Exit(MakeAccumulator(n...).Int())
}
type Intish interface {
Int() int
}
func (a Accumulator[T]) Int() int {
return int(a(0))
}
func (a Accumulator[T]) Add(x any) Accumulator[T] {
switch x := x.(type) {
case T:
a(x)
case Intish:
a(T(x.Int()))
}
return a
}
10.GO

RECURSION
FUNCTIONS THAT CALL THEMSELVES

A RECURSIVE FUNCTION CALLS ITSELF UNTIL STACK SPACE RUNS OUT
package main
func main() {
main()
}
11.GO

CALL STACK EXHAUSTION IS A NON-RECOVERABLE PANIC
package main
func main() {
defer func() {
recover()
}()
main()
}
12.GO

0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
COMPUTING FACTORIALS IS A CLASSIC RECURSIVE PROBLEM

COMPUTING FACTORIALS IS A CLASSIC RECURSIVE PROBLEM

COMPUTING MULTIPLE FACTORIALS WITH RECURSION
func main() {
if x, e := strconv.Atoi(v); e != nil || x < 0 {
fmt.Printf("no factorial defined for %vn", v)
} else {
fmt.Printf("%v! = %vn", x, Factorial(x))
}
}
}
func Factorial[T Integer](n T) T {
if n == 0 {
return 1
}
return n * Factorial(n - 1)
}
16.GO

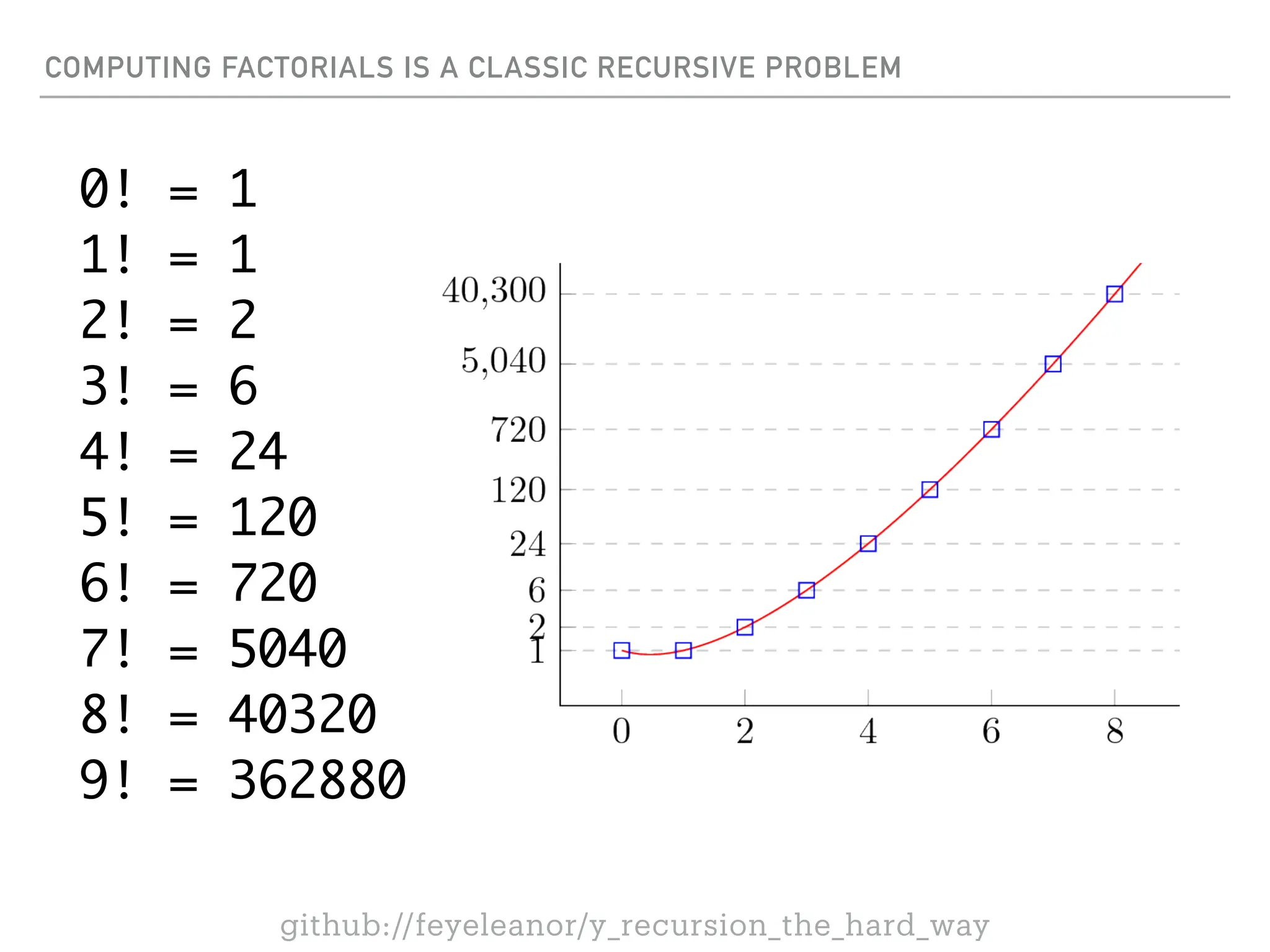
COMPUTING MULTIPLE FACTORIALS WITH RECURSION AND EXCEPTIONS
func main() {
func() {
defer func() {
if x := recover(); x != nil {
fmt.Printf("no factorial defined for %vn", x)
}
}()
if x, e := strconv.Atoi(v); e == nil && x > -1 {
} else {
panic(v)
}
}()
}
}
19.GO

SIMPLE COMPOSITION WITH HIGHER ORDER FUNCTIONS
func main() {
skipUndefined := Catch(func() {
}
})
skipUndefined(func() {
} else {
panic(v)
}
})
}
}
func Catch(e func()) func(func()) {
return func(f func()) {
defer e()
f()
}
}
20.GO

SIMPLE COMPOSITION WITH CURRYING AND HIGHER ORDER FUNCTIONS
func main() {
skipUndefined := Catch(func() {
}
})
} else {
panic(v)
}
})
}
}
defer e()
f()
}
}
20.GO

SIMPLE COMPOSITION WITH CURRYING
func main() {
skipUndefined := Catch(NoDefinedValue("factorial"))
} else {
panic(v)
}
})
}
}
defer e()
f()
}
}
func NoDefinedValue(s string) func() {
return func() {
fmt.Printf("no %v defined for %vn", s, x)
}
}
}
21.GO

SIMPLE COMPOSITION WITH CURRYING
func main() {
skipUndefined(PrintFactorial(v))
}
}
func PrintFactorial(v string) func() {
return func() {
} else {
panic(v)
}
}
}
22.GO

SIMPLE COMPOSITION WITH ANONYMOUS FUNCTIONS
func main() {
skipUndefined(
PrintFactorial(v))
}
}
func main() {
func(f func()) {
defer func(s string) {
fmt.Printf("no %v defined for %vn", s, x)
}
}("factorial")
f()
}(func() {
} else {
panic(v)
}
})
}
}
is equivalent to

USING HIGHER ORDER FUNCTIONS FOR ITERATION
func main() {
Each(os.Args[1:], func(v string) {
skipUndefined(PrintFactorial(v))
})
}
func Each[T any](s []T, f func(T)) {
if len(s) > 0 {
f(s[0])
Each(s[1:], f)
}
}
23.GO

USING HIGHER ORDER FUNCTIONS TO CACHE RESULTS
func main() {
f := MakeFactorial[int]()
skipUndefined(PrintResult(v, f))
})
}
func MakeFactorial[T Integer]() (f func(T) T) {
c := map[T] T { 0: 1 }
return func(n T) (r T) {
if n < 0 {
panic(n)
}
if r = c[n]; r == 0 {
r = n * f(n - 1)
}
c[n] = r
return
}
}
func PrintResult[T Integer](v string, f func(T) T) func() {
return func() {
if x, e := strconv.Atoi(v); e == nil {
fmt.Printf("f(%v) = %vn", x, f(T(x)))
} else {
panic(v)
}
}
}
24.GO

Y COMBINATOR
ANONYMOUS FUNCTIONS

A RECURSIVE FUNCTION CALLS ITSELF
package main
func main() {
main()
}
11.GO
this recurses because main() is a named function

A RECURSIVE FUNCTION CALLS ITSELF
package main
func main() {
func(x) {
...
}
}
but how do we make an anonymous function recurse?

ANONYMOUS FUNCTIONS AND THE LAMBDA CALCULUS

A FIXED POINT IS WHEN A FUNCTION RETURNS THE VALUE PASSED TO IT
so given f(x) = x2 - 3x + 4
f(2) = 2 is a
fi
xed point
meaning that calculating f for a value returns that value unchanged
in untyped lambda calculus functions are anonymous
but every function has a
fi
xed point
which is not the general case in mathematics

INTRODUCING THE Y COMBINATOR
Y g = (λf.(λx.f (x x)) (λx.f (x x))) g
= (λx.g (x x)) (λx.g (x x))
= g ((λx.g (x x)) (λx.g (x x)))
= g (Y g)
the Y combinator uses
fi
xed points
to express recursion
for an anonymous function

THE UNTYPED Y COMBINATOR IN THE VISUAL LANGUAGE VEX

THE UNTYPED Y COMBINATOR IN THE VISUAL LANGUAGE VEX
wtf?

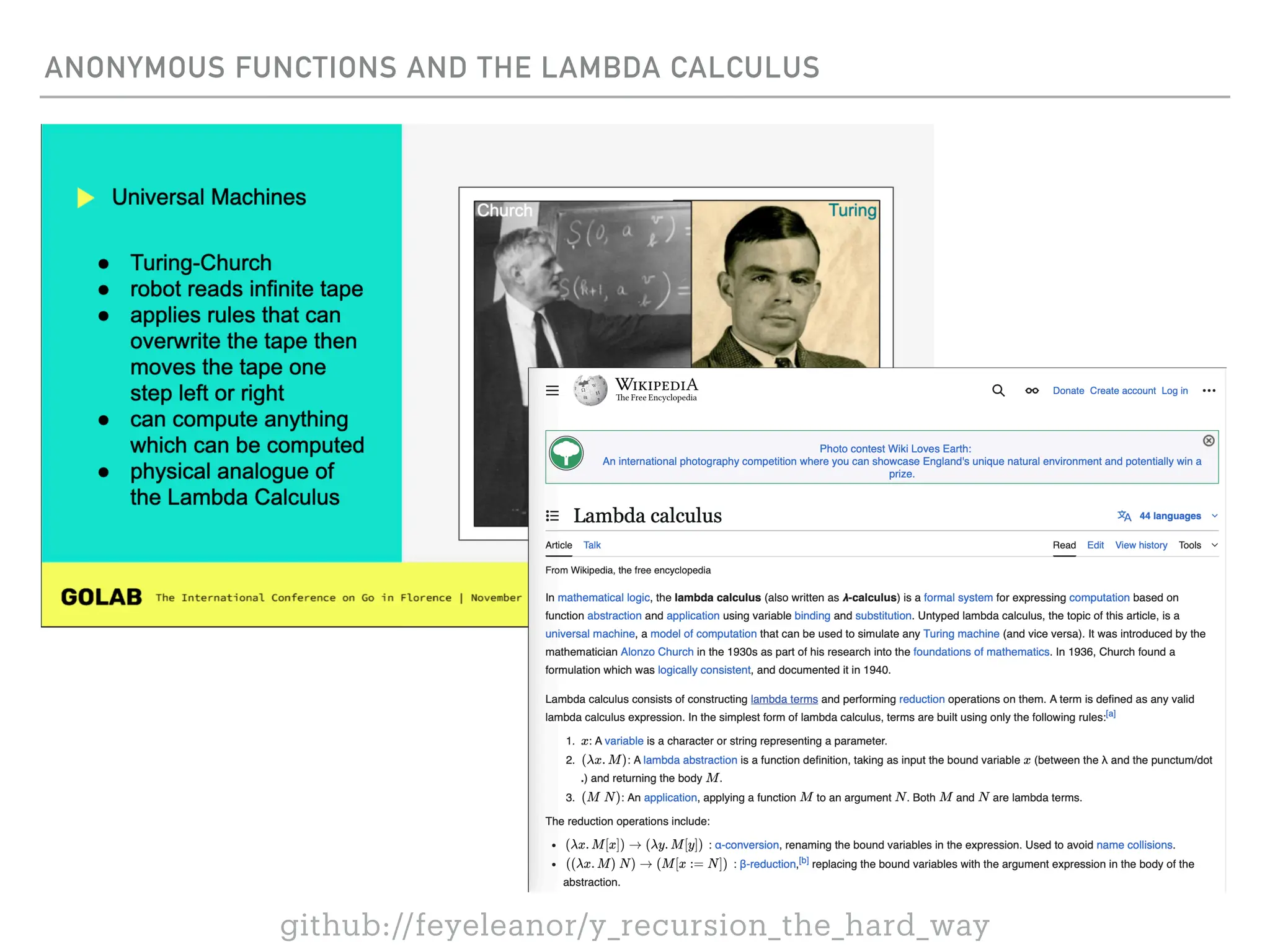
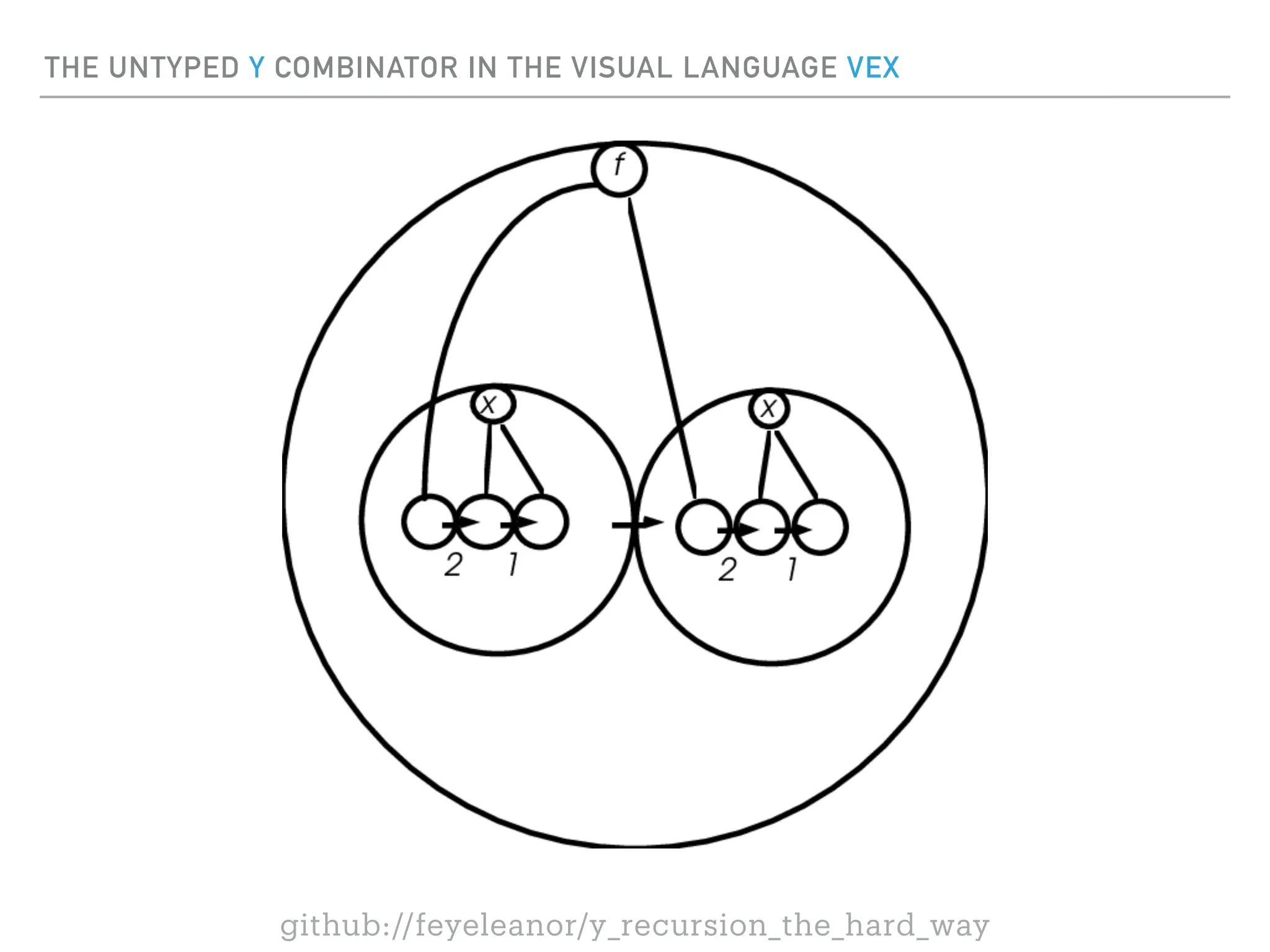
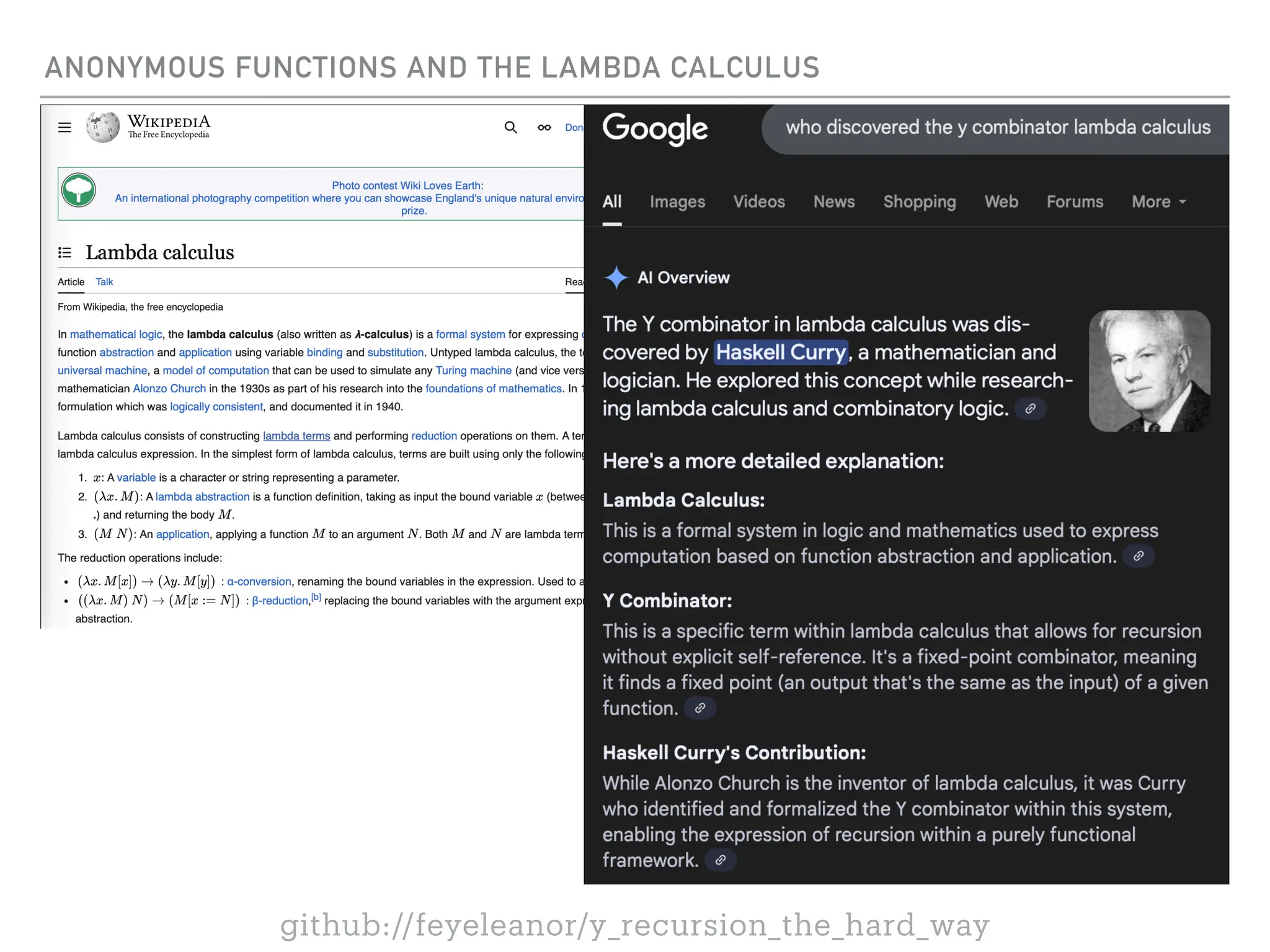
THE UNTYPED Y COMBINATOR
func main() {
factorial := Y(func(h any) any {
return func(n any) (r any) {
if n, ok := n.(int); ok {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h.(func(any) any)(n-1).(int)
}
}
panic(n)
}
})
skipUndefined(PrintResult(v, factorial))
})
}
func PrintResult(v string, f func(any) any) func() {
return func() {
fmt.Printf("f(%v) = %vn", x, f(x))
} else {
panic(v)
}
}
}
25.GO

func main() {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h.(func(any) any)(n-1).(int)
}
}
panic(n)
}
})
})
}
func Y(g func(any) any) func(any) any {
return func(f any) func(any) any {
return f.(func(any) any)(f).(func(any) any)
}(func(f any) any {
return g(func(x any) any {
return f.(func(any) any)(f).(func(any) any)(x)
})
})
}
25.GO

func main() {
...
}
})
})
}
func main() {
Catch(NoDefinedValue("factorial"))(
PrintResult(v, Y(func(h any) any {
...
}
})))
})
}
is equivalent to

INTRODUCING GO TYPES TO THE Y COMBINATOR
type Function func(any) any
func Recursor(f any) Function {
}
func Y(g Function) Function {
return Recursor(
func(f any) any {
return Recursor(f)(x)
})
})
}
func PrintResult(v string, f Function) func() {
return func() {
fmt.Printf("f(%v) = %vn", x, f(x))
} else {
panic(v)
}
}
}
26.GO

func Recursor(f any) Function {
}
func Y(g Function) Function {
return Recursor(
func(f any) any {
return Recursor(f)(x)
})
})
}
26.GO

type Transformer func(Function) Function
func Recursor(f Function) Function {
return f(f).(Function)
}
func Y(g Transformer) Function {
return Recursor(
func(f any) any {
return Recursor(f.(Function))(x)
})
})
}
27.GO

func main() {
...
factorial := Y(func(h Function) Function {
switch {
case n == 0, n == 1:
return 1
case n > 1:
return n * h(n-1).(int)
}
}
panic(n)
}
})
...
}
func Y(g Transformer) Function {
return Recursor(
func(f any) any {
return Recursor(f.(Function))(x)
})
})
}
27.GO

SIMPLIFYING THE TYPED Y COMBINATOR
Y g = (λf.(λx.f (x x)) (λx.f (x x))) g
= (λx.g (x x)) (λx.g (x x))
= g ((λx.g (x x)) (λx.g (x x)))
= g (Y g)

SIMPLIFYING THE TYPED Y COMBINATOR
type Recursor func(Recursor) Function
func (r Recursor) Apply(t Transformer) Function {
return t(r(r))
}
func Y(t Transformer) Function {
g := func(r Recursor) Function {
return func(x any) any {
return r.Apply(t)(x)
}
}
return g(g)
}
28.GO

THE Y COMBINATOR WITH GENERIC TYPES
type Function[T, R any] func(T) R
type Transformer[T, R any] func(Function[T, R]) Function[T, R]
type Recursor[T, R any] func(Recursor[T, R]) Function[T, R]
func (r Recursor[T, R]) Apply(t Transformer[T, R]) Function[T, R] {
return t(r(r))
}
func PrintResult[T, R Integer](v string, f Function[T, R]) func() {
return func() {
fmt.Printf("f(%v) = %vn", x, f(T(x)))
} else {
panic(v)
}
}
}
29.GO

THE Y COMBINATOR WITH GENERIC TYPES
type Function[T, R any] func(T) R
type Transformer[T, R any] func(Function[T, R]) Function[T, R]
type Recursor[T, R any] func(Recursor[T, R]) Function[T, R]
func (r Recursor[T, R]) Apply(t Transformer[T, R]) Function[T, R] {
return t(r(r))
}
func main() {
...
factorial := Y(func(h Function[int, int]) Function[int, int] {
return func(n int) (r int) {
switch {
case n < 0:
panic(n)
case n > 1:
return n * h(n - 1)
}
return 1
}
})
...
}
29.GO

THE GENERIC Y COMBINATOR WITH AUTOMATIC RESULT CACHING
func Y[T comparable, R any](t Transformer[T, R]) Function[T, R] {
m := make(map[T]R)
g := func(r Recursor[T, R]) Function[T, R] {
return func(x T) (v R) {
var ok bool
if v, ok = m[x]; ok {
return v
}
v = r.Apply(t)(x)
m[x] = v
fmt.Printf("Y: setting m[%v] = %vn", x, v)
return v
}
}
return g(g)
}
30.GO

func MakeY[T comparable, R any](m map[T]R) func(Transformer[T, R]) Function[T, R] {
return func(t Transformer[T, R]) Function[T, R] {
g := func(r Recursor[T, R]) Function[T, R] {
return func(x T) (v R) {
var ok bool
if v, ok = m[x]; ok {
return v
}
v = r.Apply(t)(x)
m[x] = v
fmt.Printf("Y: setting m[%v] = %vn", x, v)
return v
}
}
return g(g)
}
}
31.GO

func main() {
factorial := func(h Function[int, int]) Function[int, int] {
return func(n int) (r int) {
switch {
case n < 0:
panic(n)
case n > 1:
return n * h(n - 1)
}
return 1
}
}
m := make(map[int]int)
skipUndefined(PrintResult(v, MakeY(m)(factorial)))
})
skipUndefined(PrintResult(v, MakeY(m)(factorial)))
})
}
31.GO

LEANPUB://GONOTEBOOK [GITHUB | SLIDESHARE]://FEYELEANOR

Y - Recursion The Hard Way GopherCon EU 2025

More Related Content

Similar to Y - Recursion The Hard Way GopherCon EU 2025

More from Eleanor McHugh

Recently uploaded

Y - Recursion The Hard Way GopherCon EU 2025