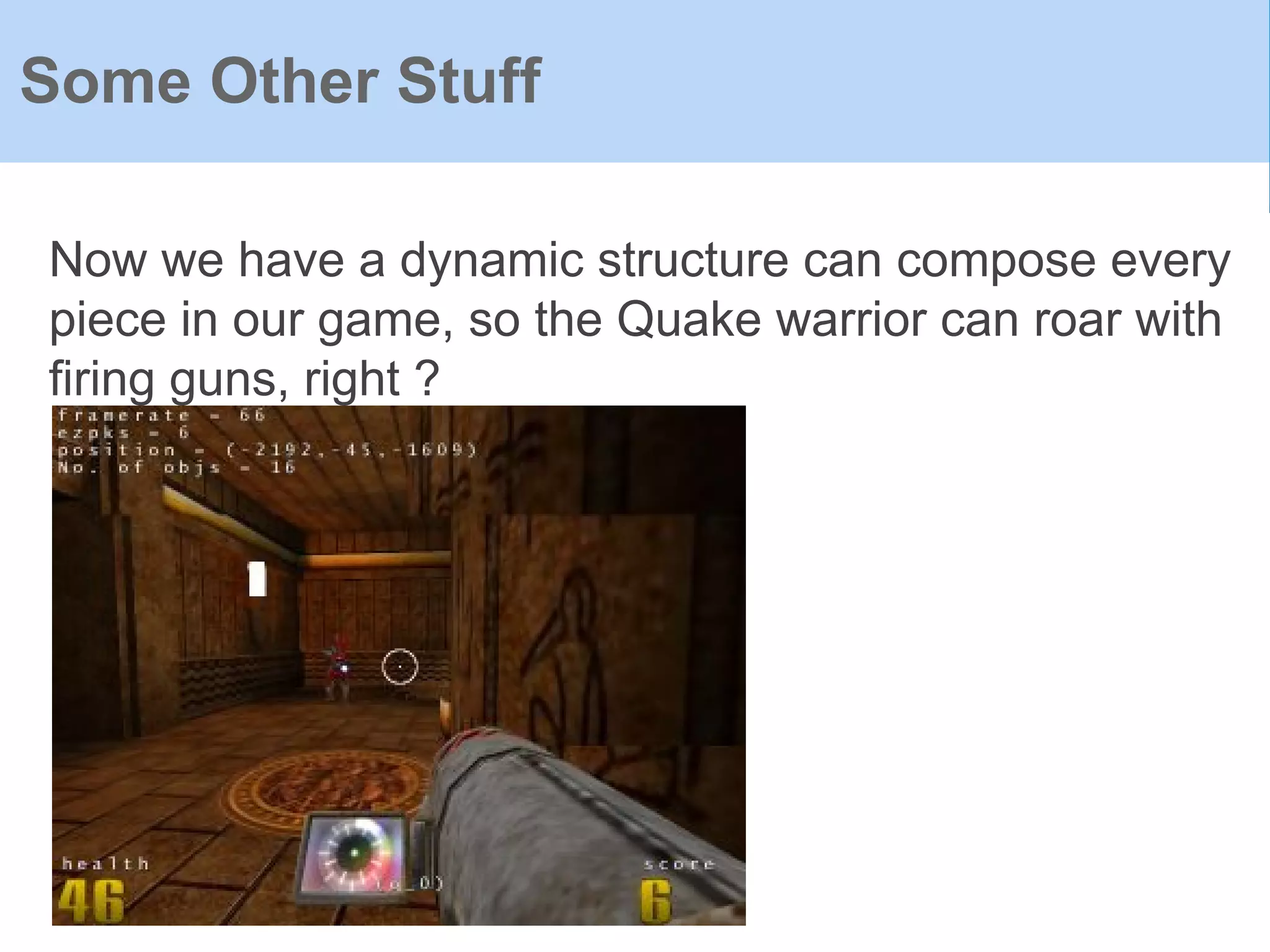
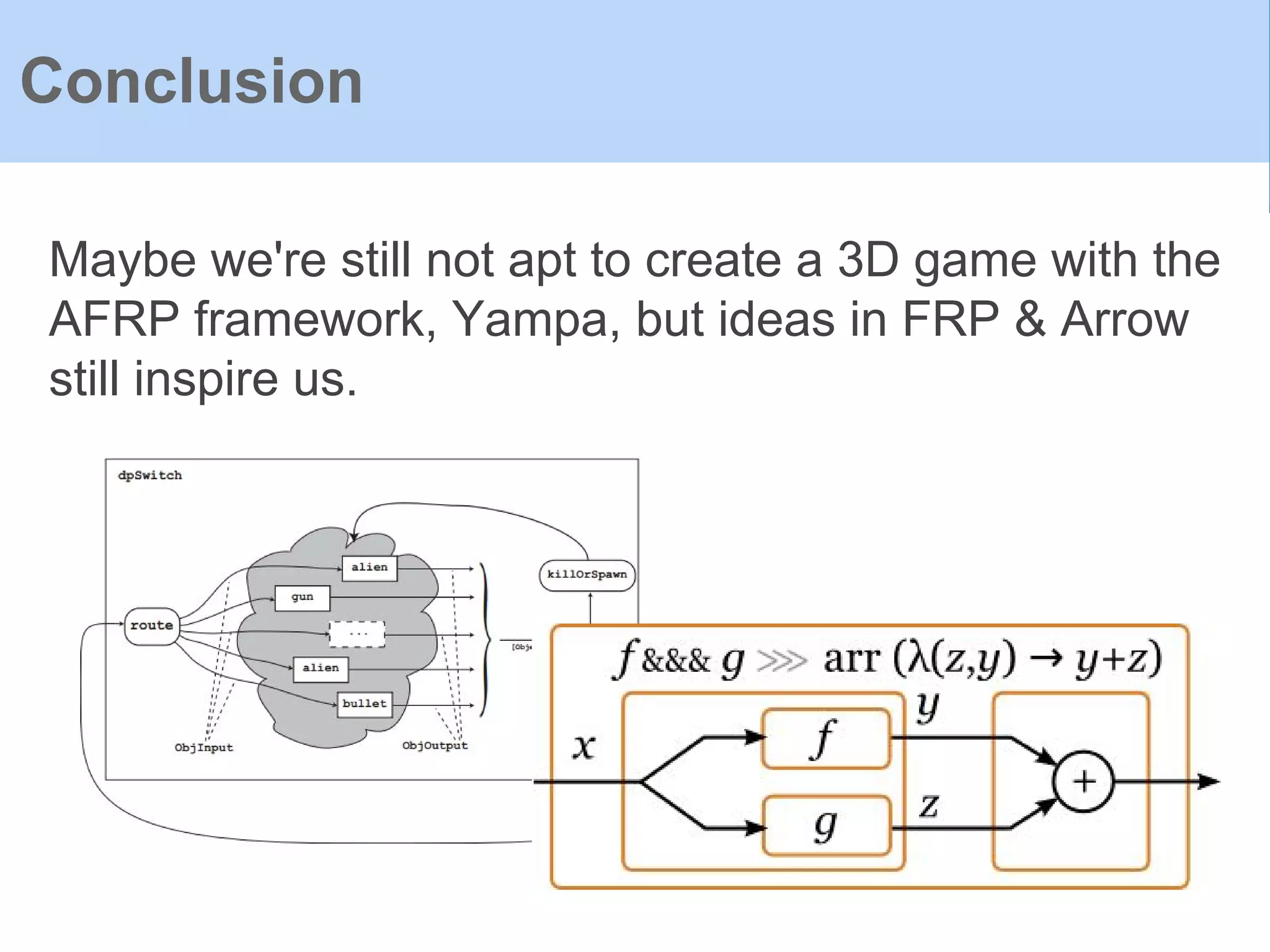
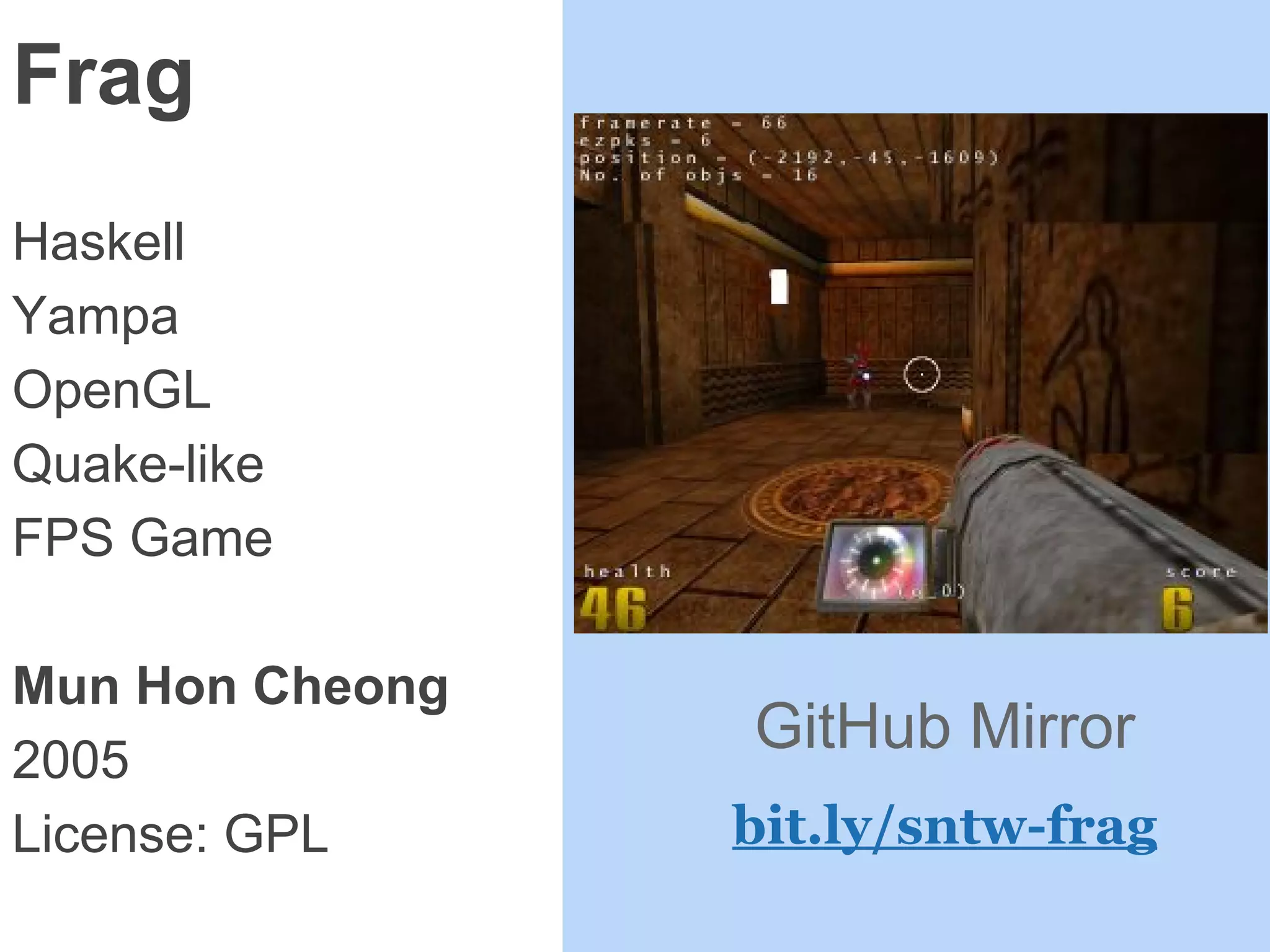
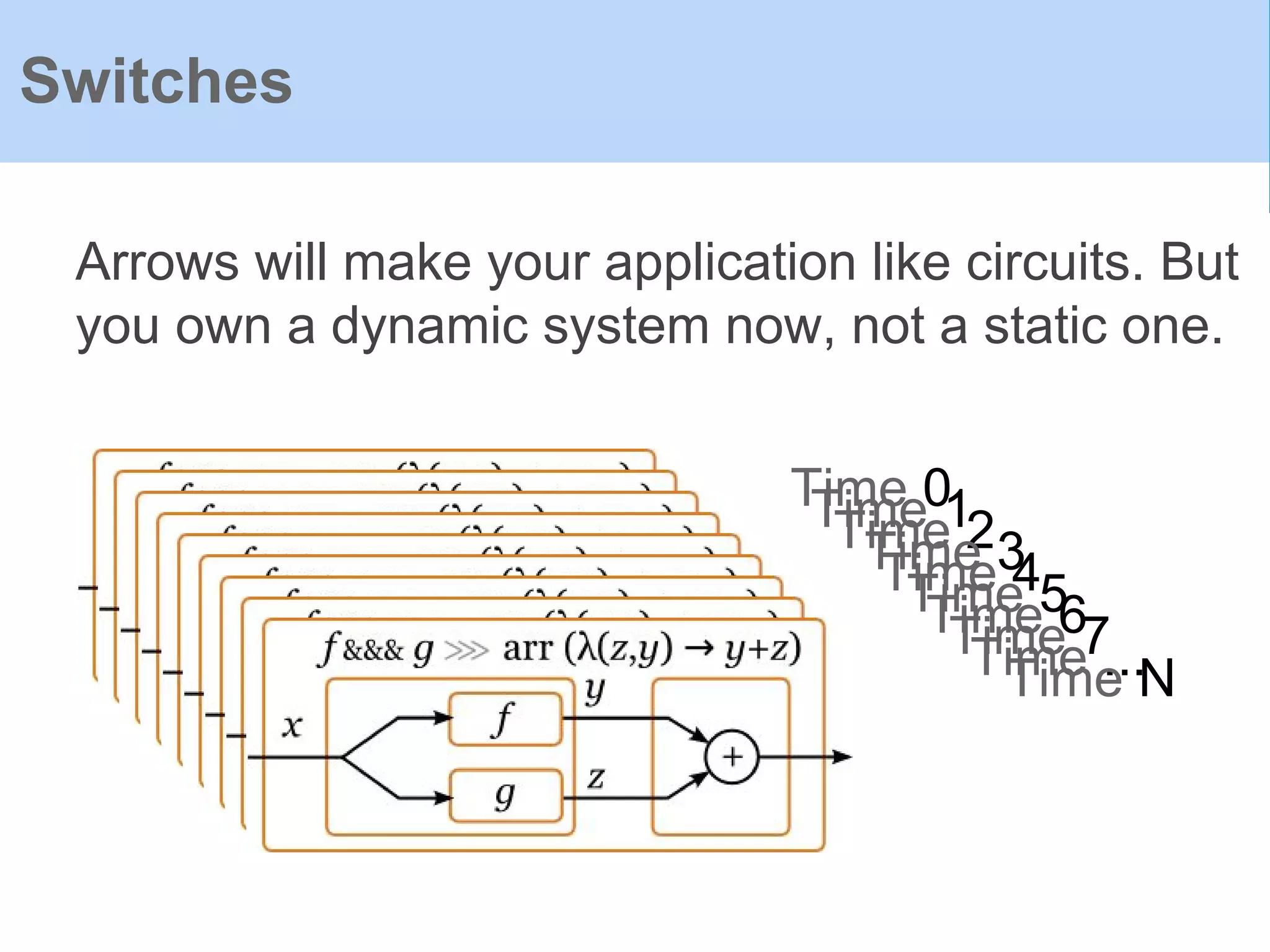
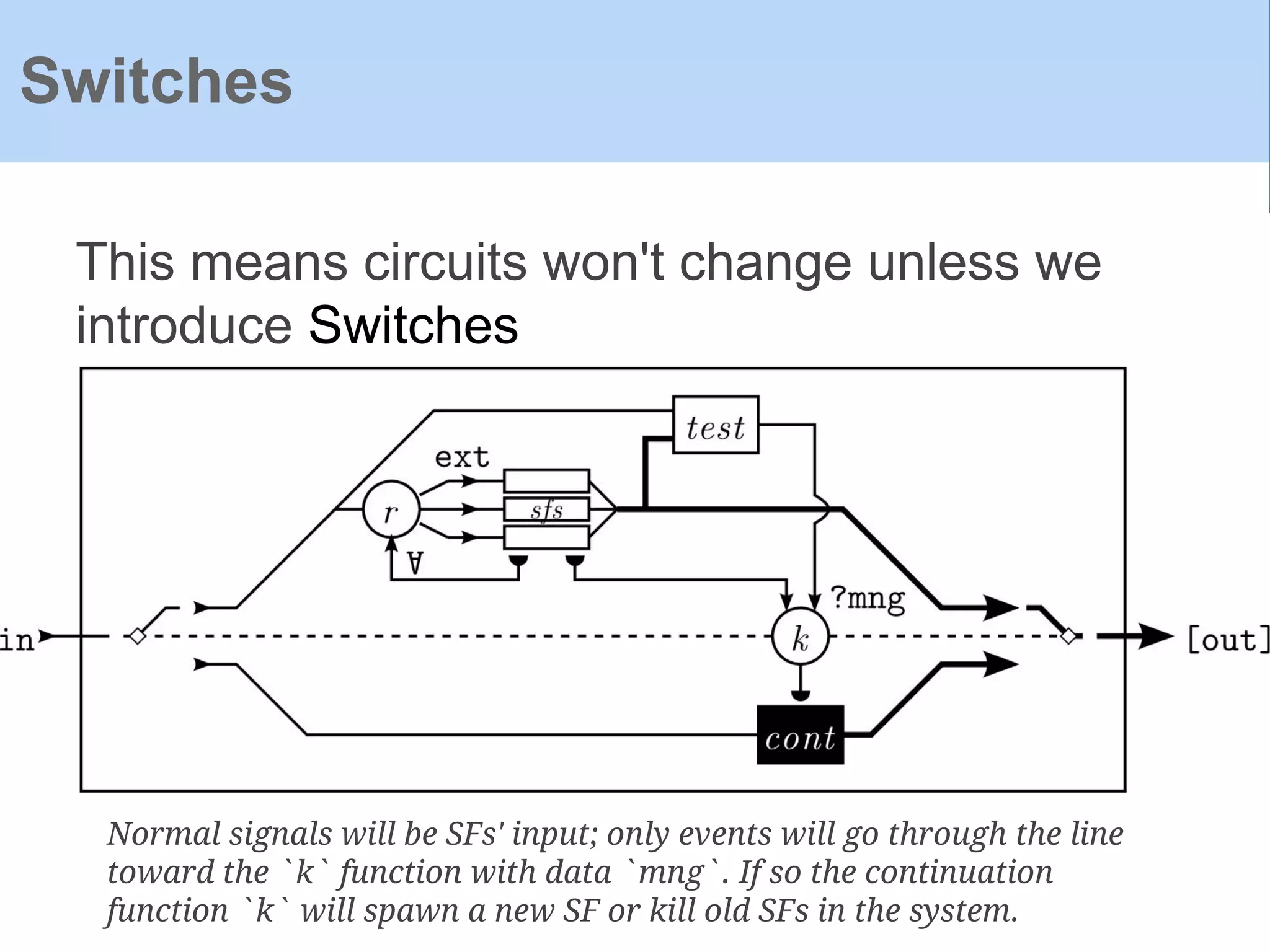
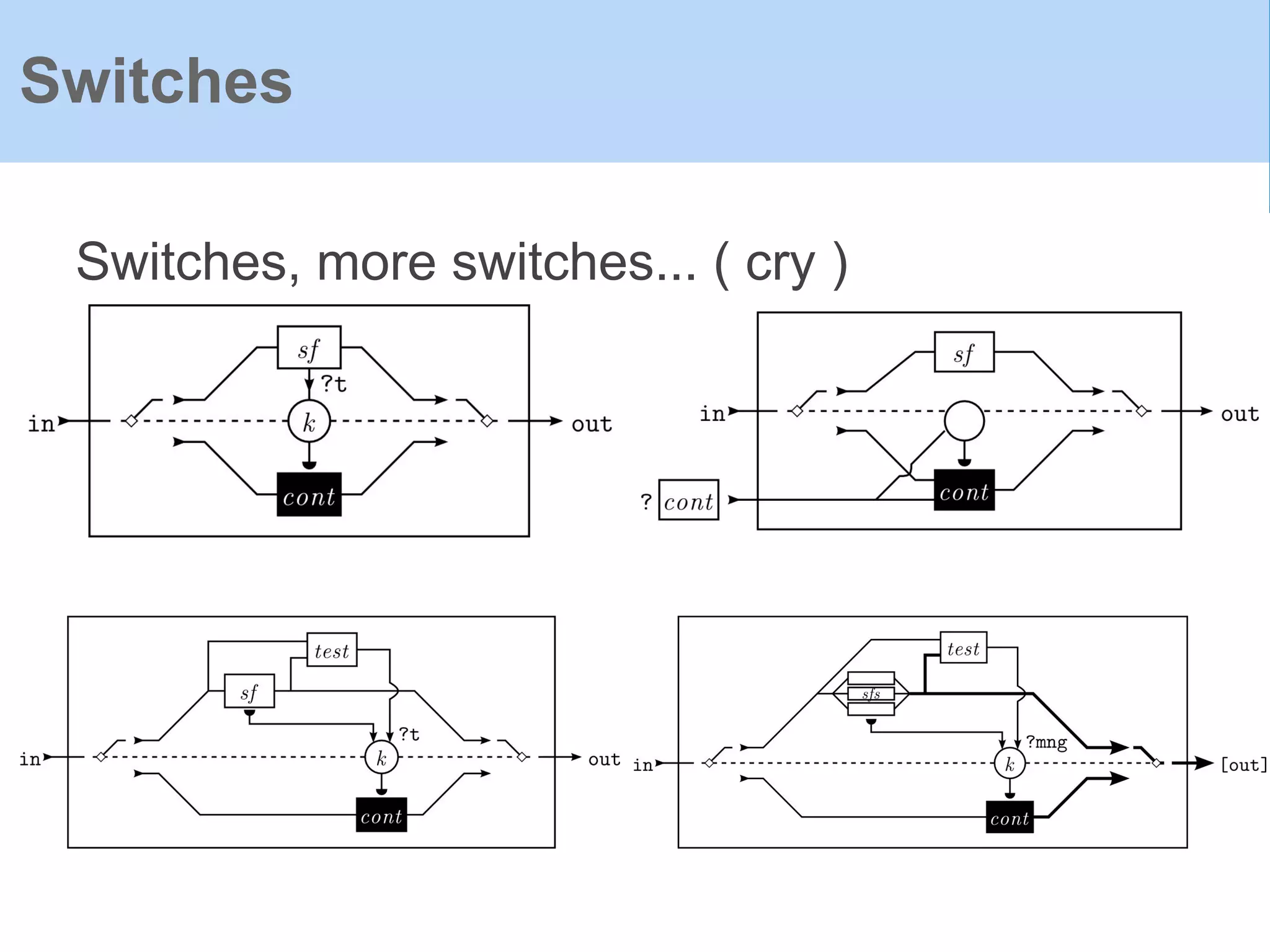
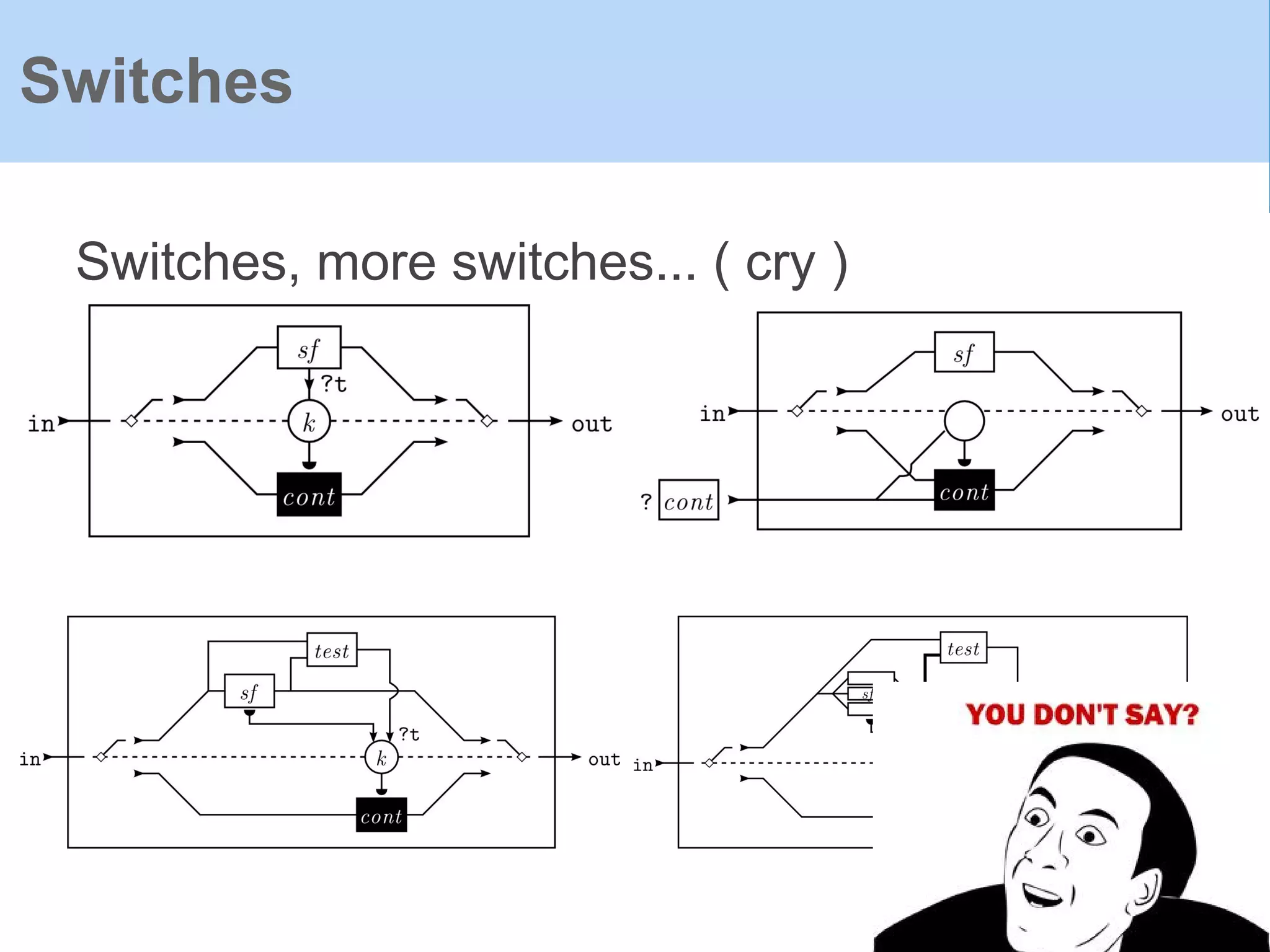
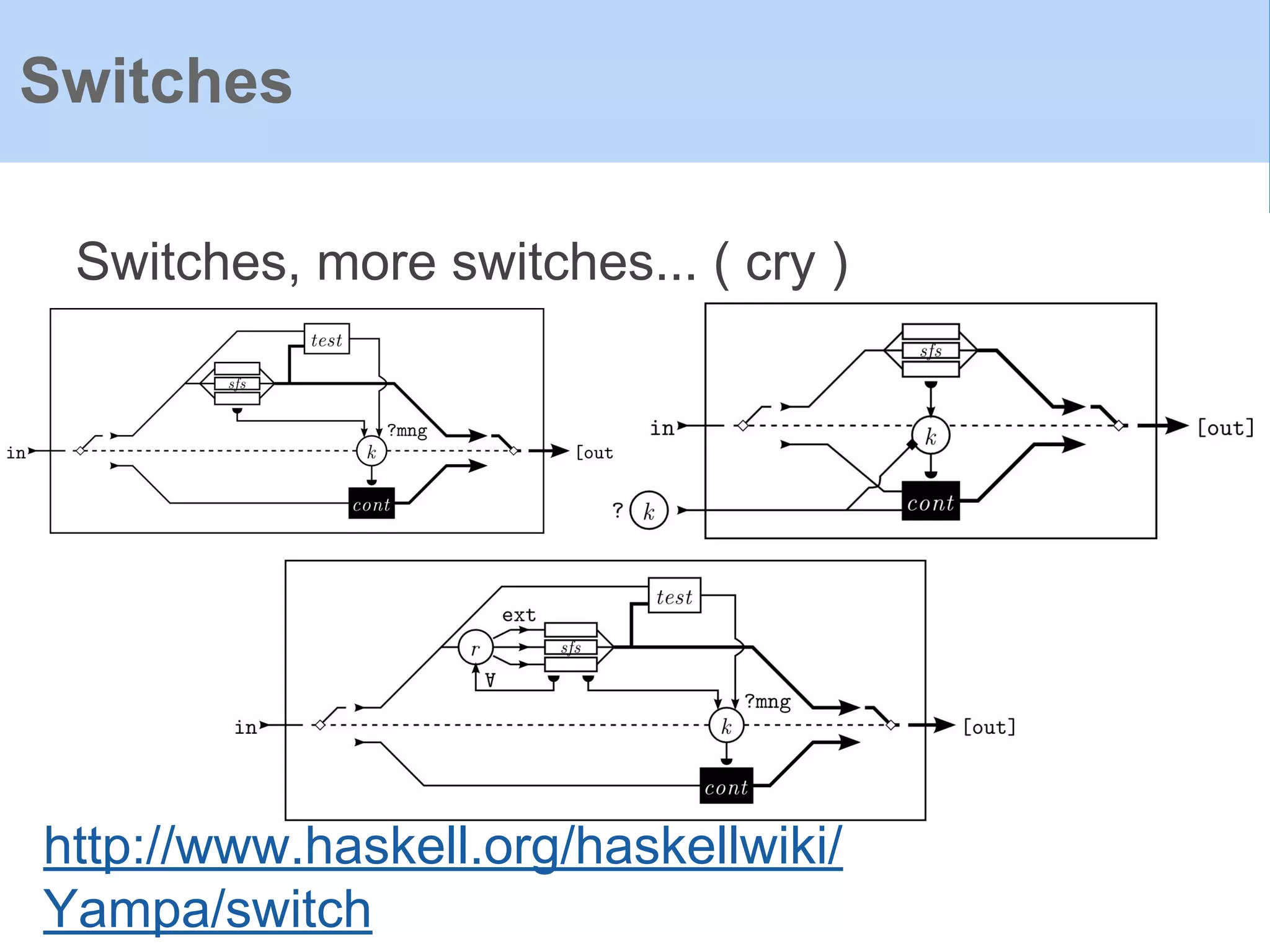
The document provides an introduction to Functional Reactive Programming (FRP) using Haskell, with a specific focus on the Yampa library for developing interactive applications like games. It discusses concepts such as signal functions, event handling, and the potential for memory leaks in FRP due to improper expressions, illustrating how to manage these via arrows in Haskell. The content emphasizes the importance of treating time as an implicit input and presents practical examples to demonstrate the concepts discussed.









![In order to perform stateful computations, we
must represent our signals in FRP as streams:
Functional Reactive Programming
newtype S a = S ([DTime] → [a])
newtype C a = C (a, DTime → C a)
integralS :: Double → S Double → S Double
integralC :: Double → C Double → C Double
x = integralS 0 (vr + vl), where vr & vl are Signals
x = integralC 0 (vr + vl), where vr & vl are Signals](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-12-2048.jpg)
![In fact we can't touch any signal in Yampa. We
can only compose Signal Functions
f
[ state (t) ]
a ( t ) b ( t )
Signal Function
SF:: Signal a → Signal b
f:: SF a b](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-13-2048.jpg)
![f:: SF a b
The `state (t)` summarizes input history:
same `f` handle every `a` in different time
SF:: Signal a → Signal b
f
[ state (t) ]
a ( t0 )
a ( t1 )
a ( t2 )
a ( t3 )
a ( tN )
a ( .... )
b ( t0 )
b ( t1 )
b ( t2 )
b ( t3 )
b ( tN )
b ( .... )
Signal Function](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-14-2048.jpg)







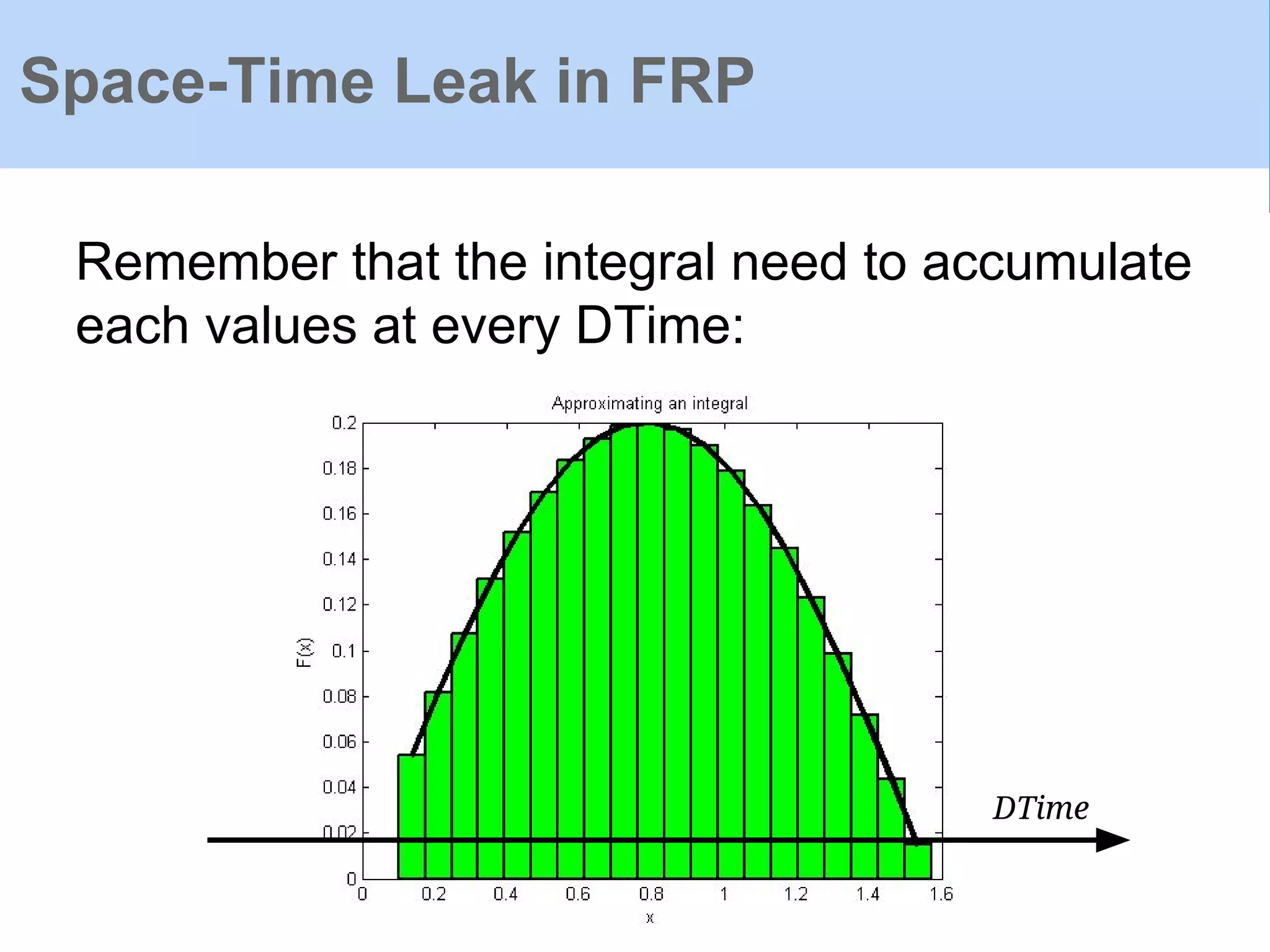
![Space-Time Leak in FRP
Because in practical systems we only care about
how to compute on continuous streams of values,
we can represent our Signals as streams in two
forms:
newtype S a = S ([DTime] → [a])
newtype C a = C (a, DTime → C a)
-- delta time, for sampling
type DTime = Double
The later one will expand its second (C a)
to make a continuing stream.](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-22-2048.jpg)





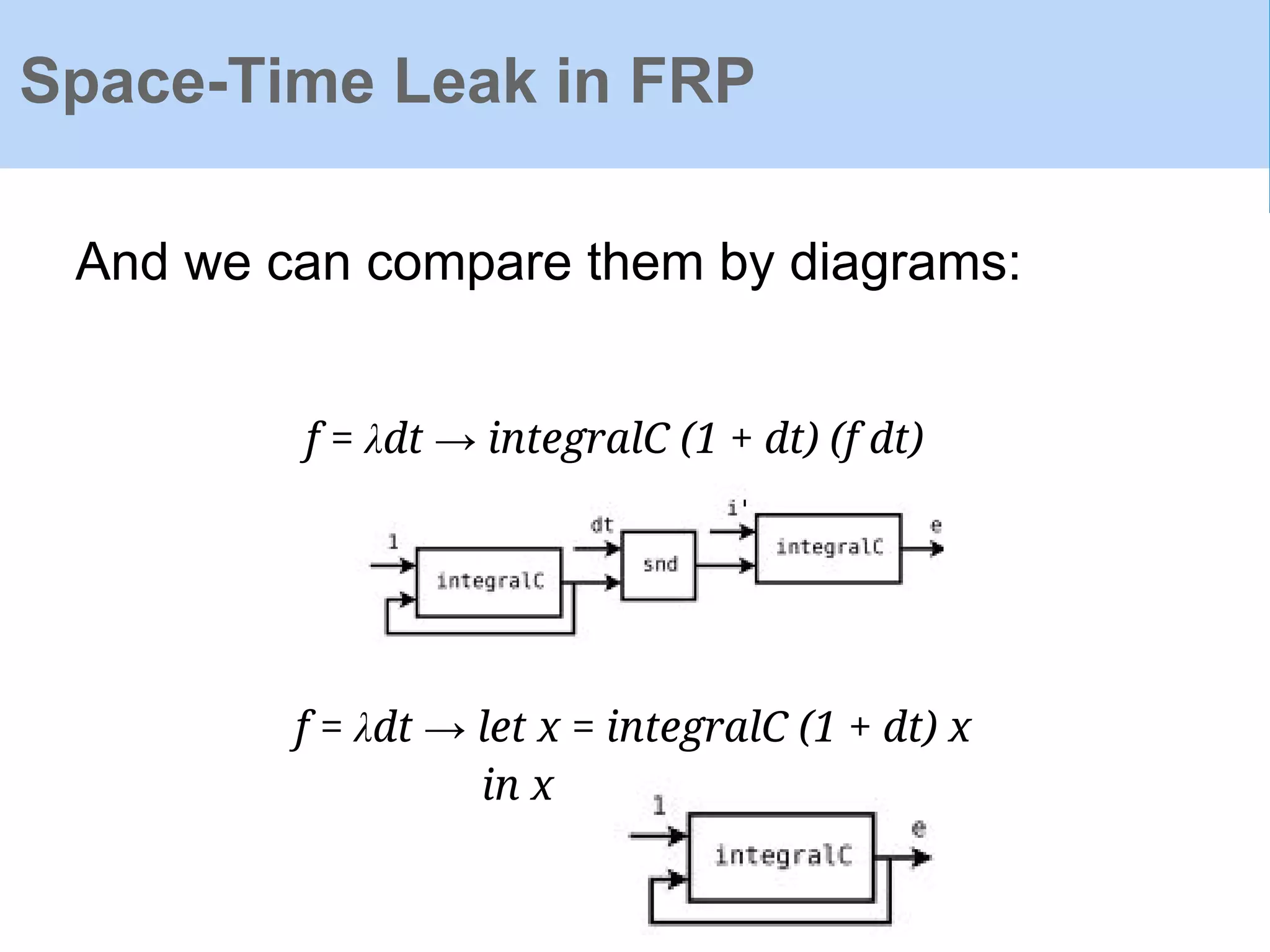
![Now we may want to "run" the stream to see what
will happen:
run :: C Double → [Double]
run (C p) = fst p : run (snd p dt)
Space-Time Leak in FRP](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-29-2048.jpg)





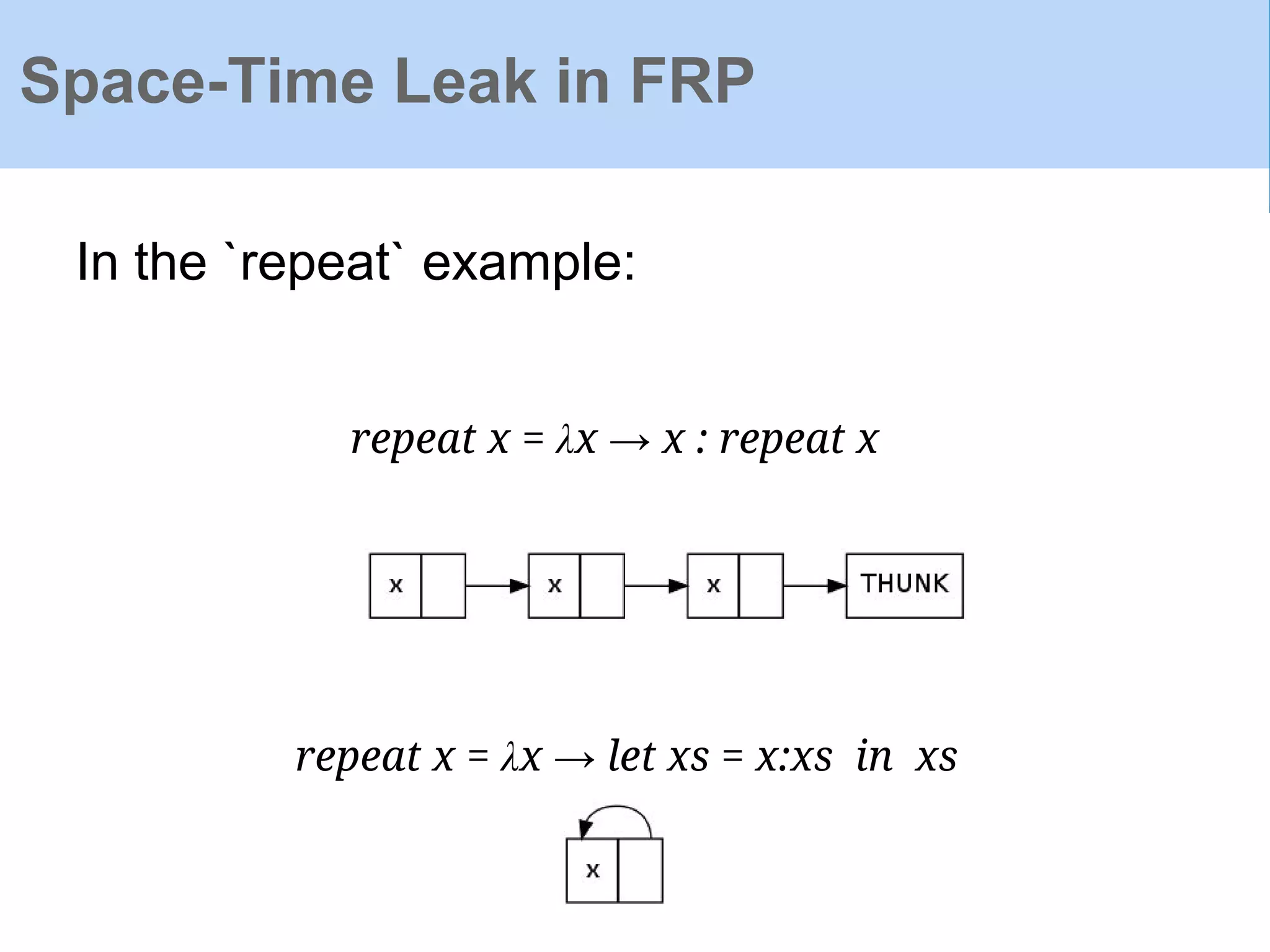


![Space-Time Leak in FRP
integralSF :: Double → SF Double Double
integralSF i = SF (λx → (i, λdt → integralSF (i + dt ∗ x)))
Now integralSF need be embedded in Arrow
structure to feed input in & run it:
e = proc () → do rec
e ← integral 1 ↢e
returnA ↢ e
runSF:: SF () Double → [Double]
runSF e](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-39-2048.jpg)













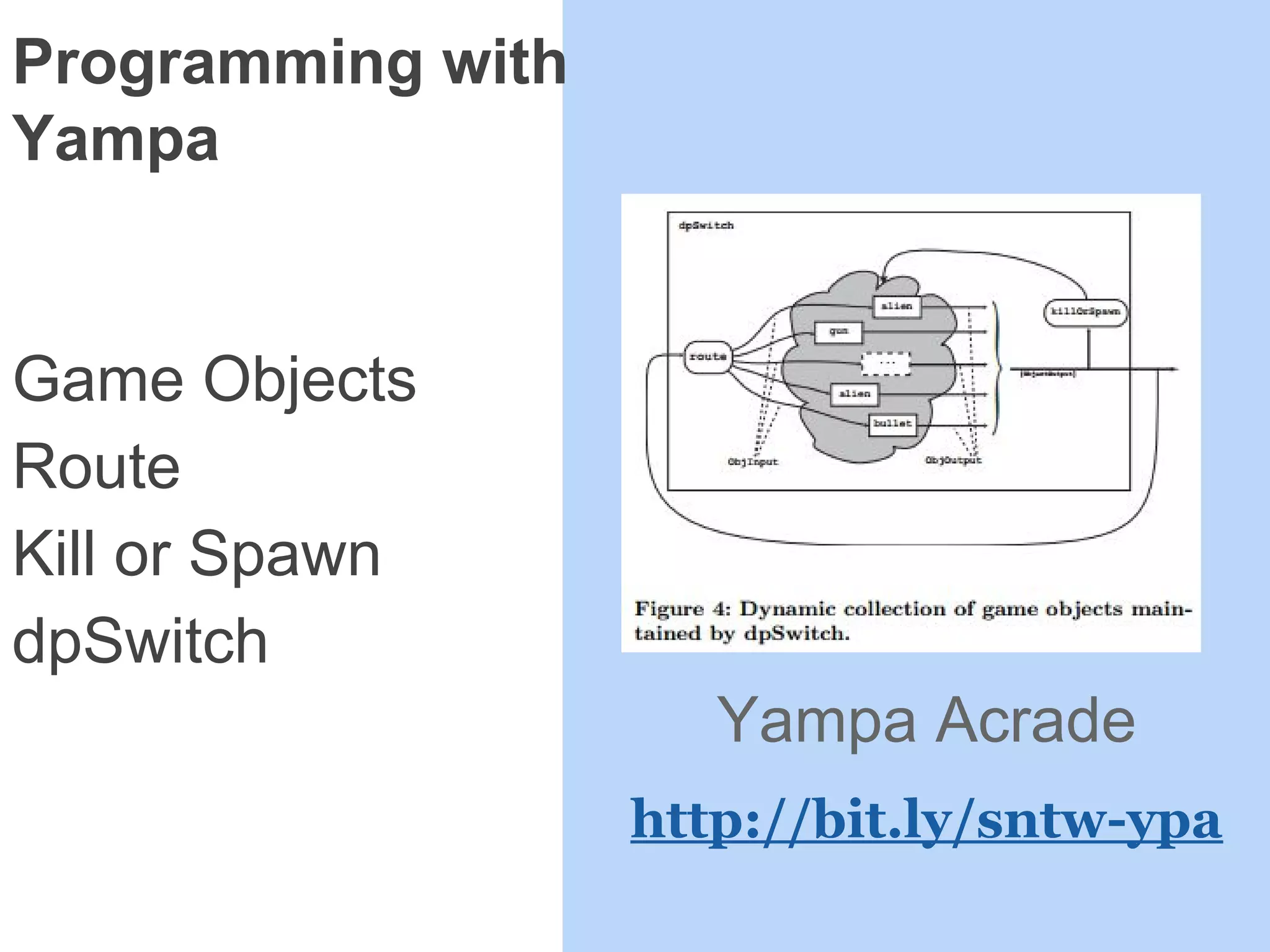


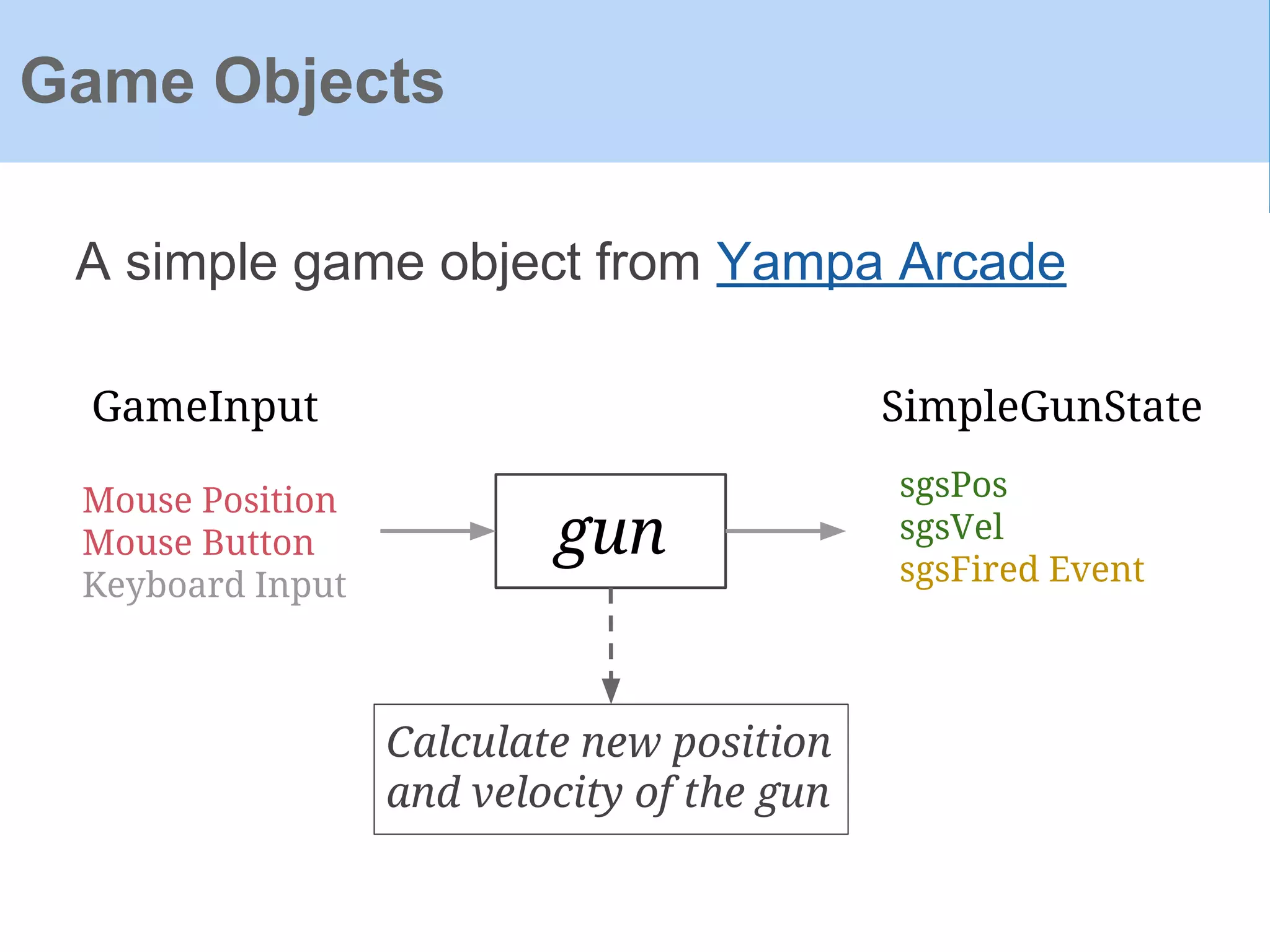
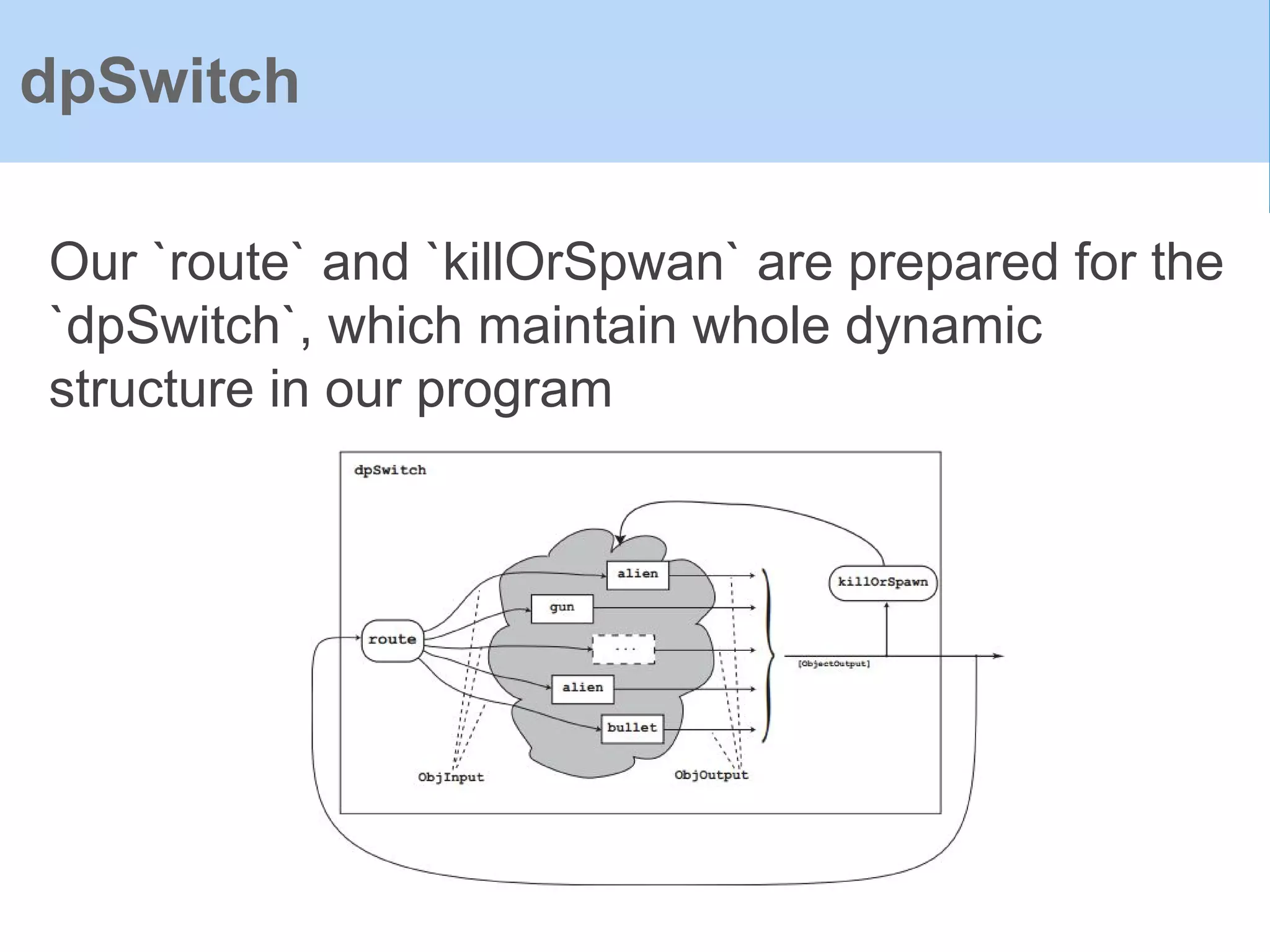
![Object inputs in Frag:
Game Objects
data ObjInput = ObjInput
{
oiHit :: !(Event [(ILKey,ObsObjState)]),
oiMessage :: !(Event [(ILKey,Message)]),
oiCollision :: !Camera,
oiCollisionPos :: !(Double,Double,Double),
oiOnLand :: !Bool,
oiGameInput :: !GameInput,
oiVisibleObjs :: !(Event [(ILKey,ObsObjState)])
}](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-70-2048.jpg)
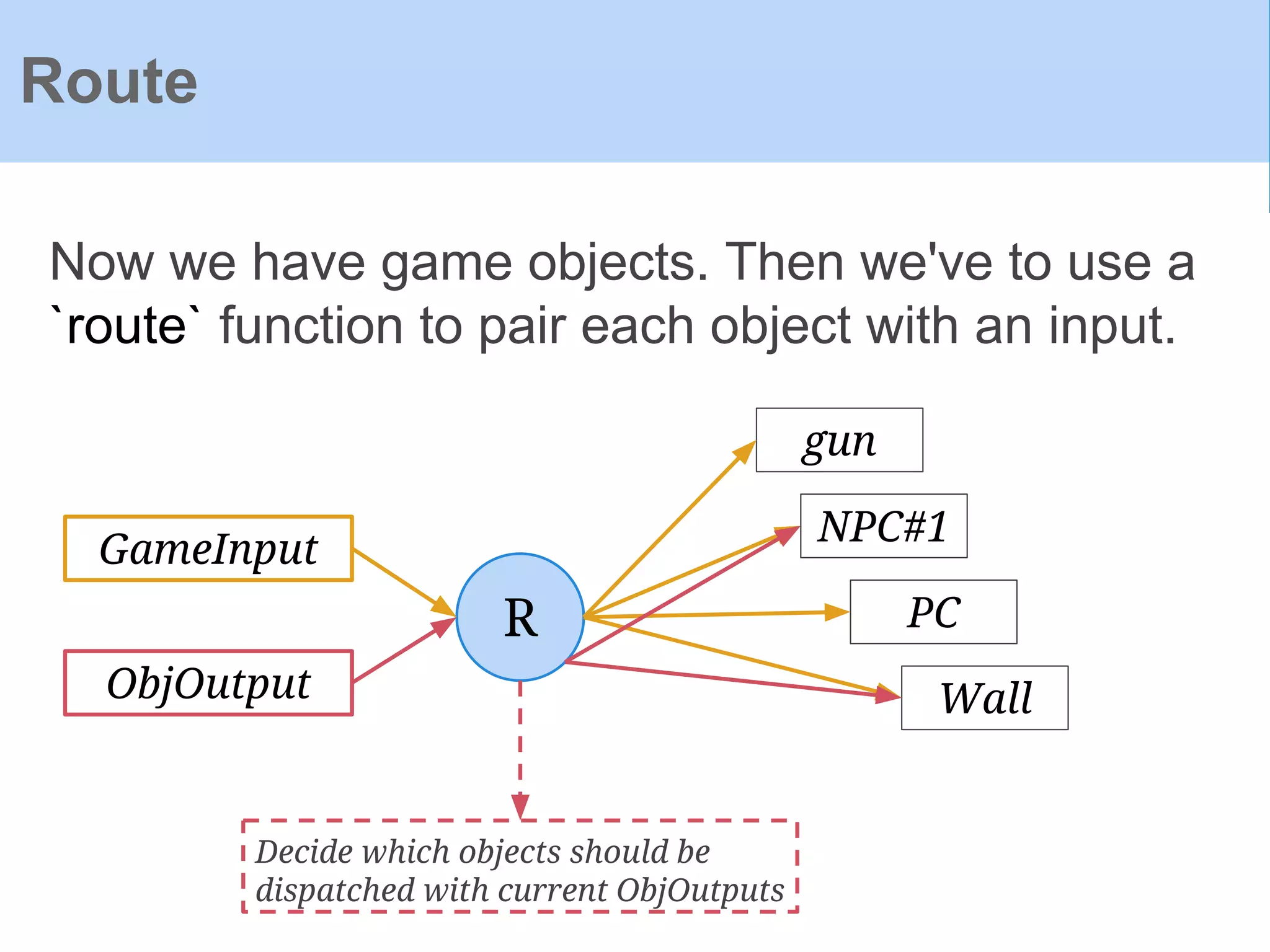
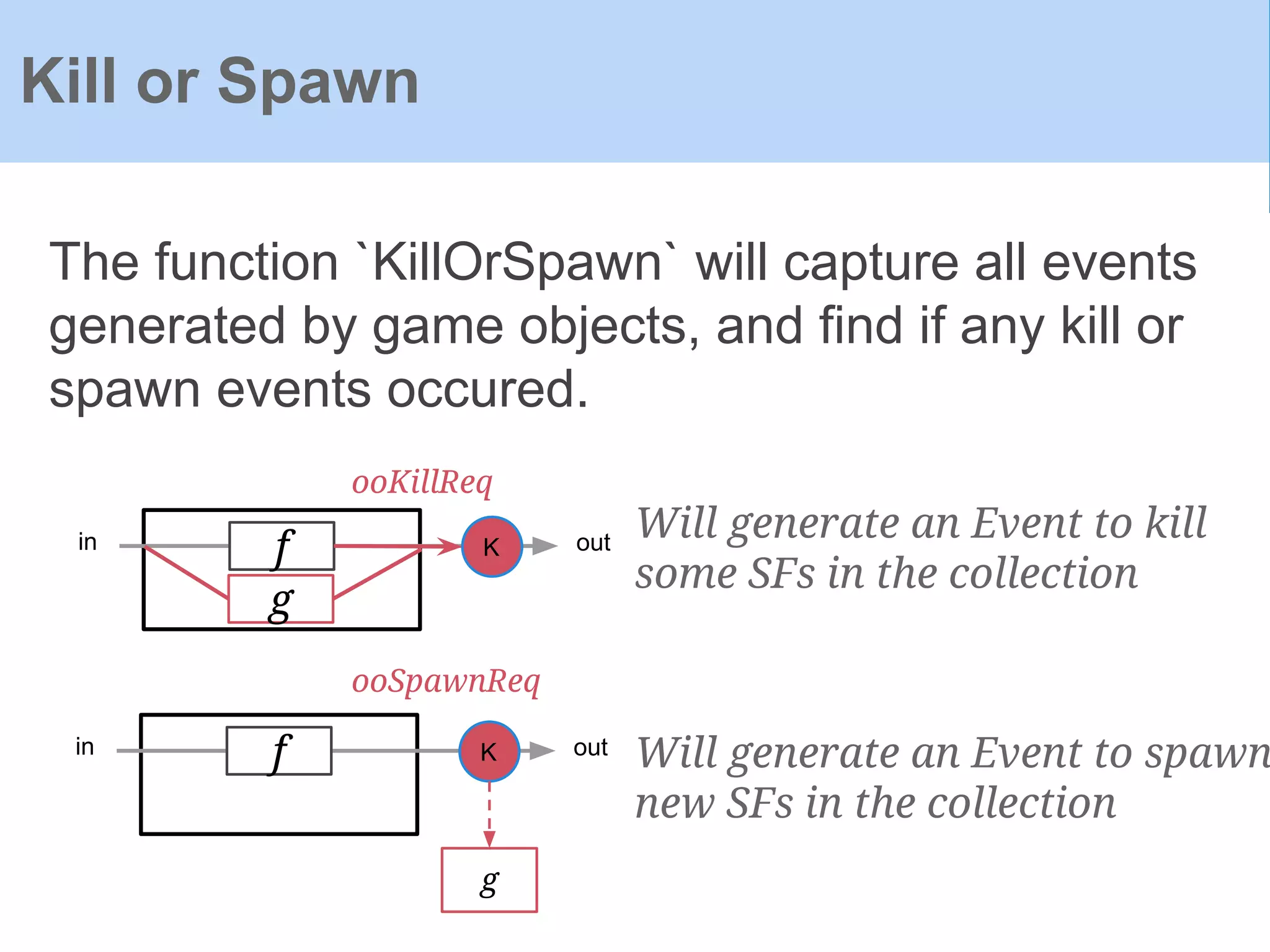
![Object outputs in Frag:
Game Objects
data ObjOutput = ObjOutput
{
ooObsObjState :: !ObsObjState,
ooSendMessage :: !(Event [(ILKey,(ILKey,Message))]),
ooKillReq :: (Event ()),
ooSpawnReq :: (Event [ILKey->Object])
}](https://image.slidesharecdn.com/yampaafrpintroduction-160602131205/75/Yampa-AFRP-Introduction-71-2048.jpg)