0% found this document useful (0 votes)
32 views2 pagesHeaviside Function: X y On 'X Axis' 'Y Axis' On Off
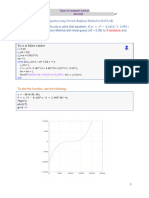
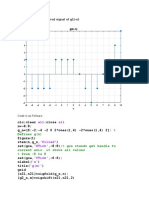
The document plots the curves (x^2 + y^2)^4 == (x^2 - y^2)^2 and x^2 - y^2 over the range [-1 1] using ezplot and sets labels and grid lines.
Uploaded by
Fakhar AbbasCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
32 views2 pagesHeaviside Function: X y On 'X Axis' 'Y Axis' On Off
The document plots the curves (x^2 + y^2)^4 == (x^2 - y^2)^2 and x^2 - y^2 over the range [-1 1] using ezplot and sets labels and grid lines.
Uploaded by
Fakhar AbbasCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 2