0% found this document useful (0 votes)
50 views29 pagesNumerical Method For Root Findings
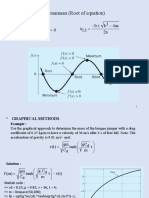
The document provides an overview of numerical methods for finding roots of polynomial equations, including techniques such as the Bisection Method and Newton-Raphson Method. It explains how to represent polynomials, find their roots using MATLAB functions, and perform operations like differentiation, integration, multiplication, and division. Additionally, it discusses curve fitting and the importance of visualizing functions to identify intervals for root finding.
Uploaded by
23ume519Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
50 views29 pagesNumerical Method For Root Findings
The document provides an overview of numerical methods for finding roots of polynomial equations, including techniques such as the Bisection Method and Newton-Raphson Method. It explains how to represent polynomials, find their roots using MATLAB functions, and perform operations like differentiation, integration, multiplication, and division. Additionally, it discusses curve fitting and the importance of visualizing functions to identify intervals for root finding.
Uploaded by
23ume519Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 29