100% found this document useful (1 vote)
135 views29 pagesAlgebra & Geometry Properties Guide
1) The document defines properties of equality, congruence, and several geometric concepts like segments, angles, and polygons.
2) Key properties include the reflexive, symmetric, and transitive properties of equality and congruence, as well as angle addition, bisection, and linear pair postulates.
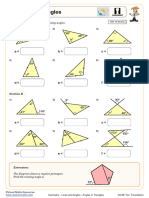
3) Formulas are given for calculating missing angle measures based on properties like the interior angles of triangles summing to 180 degrees.
Uploaded by
LA AlmznCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
100% found this document useful (1 vote)
135 views29 pagesAlgebra & Geometry Properties Guide
1) The document defines properties of equality, congruence, and several geometric concepts like segments, angles, and polygons.
2) Key properties include the reflexive, symmetric, and transitive properties of equality and congruence, as well as angle addition, bisection, and linear pair postulates.
3) Formulas are given for calculating missing angle measures based on properties like the interior angles of triangles summing to 180 degrees.
Uploaded by
LA AlmznCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 29