3/7/2014
CE 134- Design of Reinforced Concrete Structures
Chapter 8 Outline
8.1 Introduction
Chapter 8 8.2 Types of Columns
8.3 ACI/NSCP Code Requirements
Design of Columns
8.4 Axially Loaded Short Columns
8.5 Short Columns under Combined Axial Load
and Moment
Instructor: Richelle G. Zafra, PhD
Columns Axially Loaded Columns
• Columns are defined as members that carry
loads chiefly in compression.
Pier • Columns with a ratio of height-to-least lateral
dimension exceeding 3 are used primarily to
support axial compressive load.
• Columns subjected to pure axial load rarely, if
ever, exists.
Column
3 4
1
� 3/7/2014
Eccentically Loaded Columns Eccentically Loaded Columns
Columns are subjected to some bending moment Eccentric loads such as crane loads in industrial
which may be caused by unbalanced floor loads on buildings also cause moment.
both exterior and interior columns.
Crane
RC corbel
Industrial Building
5 6
Giesel Library Building, UC San Diego
Eccentically Loaded Columns Eccentically Loaded Columns
Lateral loading due to earthquake Lateral loading due to wind
Olive View Hospital,
1971 San Fernando EQ
http://www.smate.wwu.edu/teched
/geology/eq-CA-SanFernd.html
Collapsed parking structure, http://www.wbdg.org/resources/env_wind.php
California State University, Office Building Exterior and Curtain Wall,
1994 Northridge EQ pubs.usgs.gov 7 2000 Forth Worth, USA Tornado 8
2
� 3/7/2014
ACI/NSCP Code Requirements
Types of RC Columns for Tied Columns
1. Min. dimension = 200 mm
2. Min. gross area, Ag = 200 mm x 300 mm col.
= 60, 000 mm2
3. Min. main bars = 4 pcs – 16 mm ø
4. Min. clear bar cover = 40 mm (same as beams)
5. Lateral tie diameter = same method of
determining stirrup diameter
6. Gross steel ratio: ρg = 1% min. to 8% max.
9 (use only up to 4% when designing) 10
ACI/NSCP Code Requirements ACI/NSCP Code Requirements
for Tied Columns (Cont.) for Spiral Columns
7. Main bar spacing, sm
1. Min. column diameter = 250 mm
s > 1.5 main bar ø
s > 40 mm
st 2. Min. main bars = 6 pcs – 16 mm ø
s > 1.5 max size of sm 3. Min. clear bar cover = same as tied column
coarse aggregate
4. Spiral bar diameter = same as ties
8. Lateral tie spacing, st
s = 16 main bar ø 5. Gross steel ratio: ρg = same as tied column
s = 48 lateral tie ø Smallest value
6. Main bar spacing = same as tied column
s = least col. dimension
11 12
3
� 3/7/2014
ACI/NSCP Code Requirements ACI/NSCP Code Requirements
for Spiral Columns (Cont.) for Spiral Columns (Cont.)
7. Min. spiral steel percentage 8. Actual/ required spiral steel ratio
Minimum (1)
where:
Ag = gross cross-sectional area
; D = column diameter
Ac = core-concrete cross-sectional area Gross area Core concrete
; Dc = concrete core diameter/ Core Cover concrete
concrete
outside diameter of spiral 13 14
Rebar cage
ACI/NSCP Code Requirements ACI/NSCP Code Requirements
for Spiral Columns (Cont.) for Spiral Columns (Cont.)
9. Spiral pitch limits
s > 40 mm (minimum)
s < 75 mm (maximum)
s < Dc / 6
Note: To find the spiral pitch, equate req’d ρs to min ρs.
15 16
4
� 3/7/2014
Axially Loaded Short Columns Axially Loaded Short Columns
Capacity (2) where:
; for tied column = strength reduction factor
; for spiral column = gross area of section
= total area of longitudinal reinforcement
(for analysis) (3)
= specified compressive strength of concrete
where:
= specified yield strength of reinforcement
(for design) (4)
17 18
Example 1 Example 2
Design a short axially loaded square tied
A 500 mm x 500 mm tied column is
column for a service dead load of 1080 KN
reinforced with 8 - 28 mm ø bars. If f’c = 21
and a service live load of 990 KN. The
MPa and fy = 414 MPa, find the ultimate
unsupported length is 2.60 m. Use f’c = 34.5
axial capacity of the column.
MPa, fy = 414 MPa, ρg = 2 %, 25 mm ø main
bars, 10 mm ø ties, and 40 mm concrete
cover.
19 20
5
� 3/7/2014
Columns under Combined Axial Columns under Combined Axial
Load and Moment Load and Moment (Cont.)
External Forces Strain Diagram Internal Forces on Columns External Forces Strain Diagram Internal Forces on Columns
Equilibrium of external and internal axial forces Moment about section centerline of internal forces must
requires that be equal and opposite the moment of external force Pn
(5)
21 22
(6)
Columns under Combined Axial Columns under Combined Axial
Load and Moment (Cont.) Load and Moment (Cont.)
where: = nominal axial capacity If we know Neutral axis
= eccentricity (c, a)
= width of section
= height of section Strain condition
= compression steel area (εs, ε’s)
= tension steel area
= location of A’s from the compression face Stress condition
(fs, f’s)
= location of As from the compression face
= stress in the compression steel Can determine Column Strength
= stress in the tension steel 23 (Mn, Pn) 24
6
� 3/7/2014
Columns under Combined Axial Columns under Combined Axial
Load and Moment (Cont.) Load and Moment (Cont.)
Jiravacharadet (2013)
Tension Steel
External
(6) (7) Force on
Column
where:
Stress
Strain Diagram C
Compression Steel Diagram
T
(8) (9)
Concrete Stress Block
; (10) 25 26
Internal Forces on Columns
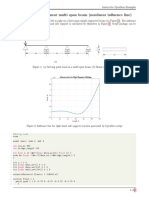
Interaction Diagram for Combined Interaction Diagram for Combined
Bending and Axial Load Bending and Axial Load
Pn • For any eccentricity Pn • Any combination of
emin emin
Po e, there is a unique Po loading that falls
pair of Pn and Mn . inside the curve is
Direct axial Direct axial
failure failure
satisfactory
(Mn, Pn) • Plotting a series of
e=0
e=0
Compression (Mn, P n) pairs Compression
• However, any
e range
failure eb corresponding to failure range eb combination falling
different e will result outside the curve
Tension failure range Tension failure range represents failure.
in an interaction
Mo Mn diagram. Mo Mn
Column Interaction Diagram Column Interaction Diagram
27 28
7
� 3/7/2014
Balanced Failure, eb Balanced Failure, eb
• Concrete reaches the strain limit εcu at the same Strain Diagram
(15)
time that the tensile steel reaches the yield strain εy
• Dividing point between compression failure (small
eccentricities) and tension failure (large
eccentricities)
Strain Diagram
where:
(11)
where: (13)
(12) (14)
29 30
Short Columns Under Combined Behavior at Failure:
Axial Load and Moment Columns under Combined P and M
A. Minimum Eccentricity Pn Pn Region I: Negligible Moment
Po Po
(Tied) e < emin
(Spiral) (Mn, Pn) Direct axial failure
e=0
e=0
(Region I)
Capacity: See axially
e
B. Actual Eccentricity loaded column
Mn eb
Mo Mn
Mo
Column Interaction Diagram
31
Column Interaction Diagram 32
8
� 3/7/2014
Behavior at Failure: Approximate Capacity Formulas
Columns under Combined P and M (Region II)
Pn Region II: Proportioned 1. From straight line relation on interaction curve
Po Axial Load and Moment
emin < e < eb (16)
e=0
Compression
failure range
Capacity: Pn > Pb
(Region II)
eb
Mn
Mo
Column Interaction Diagram 33 34
Approximate Capacity Formulas Behavior at Failure:
(Region II) Columns under Combined P and M
2. Whitney’s Formula Pn Region III: Proportioned
Po Axial Load and Moment
(17) Tied
Column e > eb
e=0
Capacity: Pn < Pb
eb
(18) Spiral Tension failure range
Column (Region III)
Mo Mn
35
Column Interaction Diagram 36
9
� 3/7/2014
Approximate Capacity Formulas Approximate Capacity Formulas
(Region III) (Region III)
Approximate Whitney’s Capacity Formulas (Tied Columns)
Approximate Whitney’s Capacity Formulas (Spiral Columns)
(19)
where: ; As = bars in tension (20)
37 38
Example 3 y Biaxial Bending
e
For the column shown As As’ • Axial compression is
3-28mmφ
3-28mmφ
with f’c = 28 MPa and fy =
300 mm
Pn accompanied by simultaneous
414 MPa, determine: bending about both principal
x
• ultimate axial capacity axes of the section.
at balanced condition; 62.5 187.5 187.5 62.5 • Such is the case of corner nees-anchor.ceas.uwm.edu
• load eccentricity at 500 mm columns of tier buildings
balanced condition; Top View where beams and girders
• ultimate axial capacity if e frame into the columns in both
e = 200 mm. Pn directions and transfer their
end moments into the
Bending is about y-axis of columns in two perpendicular
39 nisee.berkeley.edu 40
the column. Elevation View planes.
10
� 3/7/2014
Strength Interaction Diagram for
Biaxial Bending Reciprocal Load Method
Uniaxial bending • A simple, approximate design method
about Y axis developed by Bresler.
• Acceptably accurate for design purposes
Uniaxial bending provided
about X axis
Biaxial bending
41 42
Column Interaction Diagram
Reciprocal Load Method Example 4
Bresler’s reciprocal load equation is given by
Using Bresler’s equation,
(21) y
determine the strength of
the column shown given
300 mm
where:
= approximate value of nominal load in biaxial the biaxial capacities Pnx =
8-20mmφ x
bending with eccentricities ex and ey 1880 KN, Pny = 1000 KN,
= nominal load when only eccentricity ex is f’c = 21 MPa, fy = 414
MPa. 200 mm 200 mm
present (ey = 0)
= nominal load when only eccentricity ey is
present (ex = 0)
= load for concentrically loaded column 43 44
11
� 3/7/2014
Use of Column Interaction Use of Column Interaction
Diagram for Design Diagram for Design
engmechanics.blogspot.com
• The preceding lectures have clearly shown that
the analysis and design of columns with ρg e/h
eccentricities using static equations is very
tedious and complicated.
• Consequently, designers resort almost
completely to tables, computers, or diagrams (e. (ksi)
g. column interaction diagram) for their column
calculations.
• Interaction diagrams are useful for studying
strength of columns with varying proportions of
loads and moment. 45 (ksi)
46
How to Use Column Interaction Use of Column Interaction
Diagram for Design Diagram
In order to correctly use the Note:
column interaction diagram, it • Both x and h should be taken in the direction of
is necessary to compute the bending.
h
value of γ
γh • In using the column interaction diagram, be sure
that the column picture at the upper right of the
where:
b diagram being used agrees with the column
being considered.
γh = center to center distance
of bars on each side of • For example, are there bars on two faces of the
the column column or on all four faces?
h = column depth 47 48
12
� 3/7/2014
Column Interaction Diagram
Example 5 (Rectangular Section)
Calculate the nominal e
axial capacity (in kN) of
the column shown if the
4-25mmφ
4-25mmφ
400 mm
eccentricity of the load
Pn
is 200 mm. Use f’c = 21
MPa and fy = 414 MPa.
Use the interaction
diagram. 75 450 75
600 mm 1.2 ksi
49 50
Column Interaction Diagram
Example 6 (Circular Section)
Calculate the nominal
axial load (in kN) that
62.5
e
can be applied in the
column at an
eccentricity of 200
500 mm
375
mm. Use f’c = 28 MPa Pn 8-22mmφ
and fy = 414 MPa.
Use the interaction
diagram.
62.5
1.0 ksi
51 52
13
� 3/7/2014
Column Interaction Diagram
Example 7 (Rectangular Section)
Calculate the nominal e
axial load (in kN) that can
be applied in the column
500 mm
at an eccentricity of 400 16-28mmφ Pn
mm. Use f’c = 21 MPa and
fy = 414 MPa. Use the
interaction diagram.
70 360 70
500 mm 0.65 ksi
53 54
Column Interaction Diagram
(Rectangular Section) References
Jiravacharadet, M. Lecture Notes in Reinforced
Concrete Columns. School of Civil Engineering,
Suranaree University of Technology, Thailand.
Accessed June 10, 2013.
Nilson, A. H. 1997. Design of Concrete
th
Structures. 12 Edition. McGraw-Hill: Singapore.
McCormac, J. C. and Nelson, J.K. 2005. Design
of Reinforced Concrete. 6th Edition. John Wiley &
0.82 ksi Sons, Inc: New Jersey.
55 56
14