100% found this document useful (1 vote)
235 views5 pagesl-10 Lines and Angles
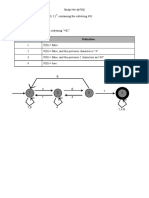
This document provides definitions and descriptions of key geometry terms:
- It defines points, lines, line segments, rays, planes, angles, and different types of angles and triangles.
- It explains properties of lines and angles, including that two lines can intersect in at most one point, and the angle measurements for acute, right, obtuse, straight, and reflex angles.
- It describes relationships between angles, such as complementary, supplementary, adjacent, corresponding, alternate, and vertically opposite angles.
- The document also summarizes triangle properties, like the three interior angles summing to 180 degrees and the exterior angle theorem.
Uploaded by
Swetha PoojaryCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
100% found this document useful (1 vote)
235 views5 pagesl-10 Lines and Angles
This document provides definitions and descriptions of key geometry terms:
- It defines points, lines, line segments, rays, planes, angles, and different types of angles and triangles.
- It explains properties of lines and angles, including that two lines can intersect in at most one point, and the angle measurements for acute, right, obtuse, straight, and reflex angles.
- It describes relationships between angles, such as complementary, supplementary, adjacent, corresponding, alternate, and vertically opposite angles.
- The document also summarizes triangle properties, like the three interior angles summing to 180 degrees and the exterior angle theorem.
Uploaded by
Swetha PoojaryCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 5