—— Further Engineering MathematicsTe] 326 Getting to know your unit Alfesfment This wit will be assessed by a series of assignments set by your tutor. ‘Mathematics is a way in which engineers model the world around them and test their ideas and designs before these become real products, Statistics might be used during manufacturing processes as part of the quality control (QC) system and to determine the in-service reliability of product. As an engineer you need to understand and develop the skills required to solve complex problems and analyse data. How you will be assessed This unit will be assessed by a series of internally assessed tasks set by your tutor Throughout this unit you will find assessment activities to help you work towards your assessment. Completing these activities will mean that you carried out useful research or preparation that will be relevant when it comes to your final assignment. In order for you to achieve the tasks in your assignment, itis important to check that you have met all ofthe assessment criteria. You can do this as you work your way through the assignment, The assignments set by your tutor will consist of a number of tasks designed to meet the criteria in the table. Further Engineering MathematicsGetting to know your unit ue This table shows what you must do in order to achieve a Pass, Merit or Distinction grade, and where you can find activities to help you. Pass Merit Distinction tearing atm I caine ow sequences eres can bed Solve given problems using _Solve given problems accurately using _Evaluate, using technically correct language and a routine arithmetic and geometric routine and non-routine arithmetic and _logical structure, engineering problems using non- progression operations ‘geometric progression operations. routine sequence and series operations, while solving ‘Assossment practice 8.1 ‘Assessment practice 8.1 all the given problems accurately using routine and non-routine operations. ‘Assossment practice 8.1 Sppewapewy Sussaui8ey vaepang Solve given problems using _ Solve given problems accurately using routine power series operations. routine and non-routine power series ‘Assossment practice 8.1 operations. ‘Assessment practice 8.1 Learning aim ff} Examine how matrices and determinants can be used to solve engineering problems =a Solve given problems Solve given problems accurately using _Evaluate, using technically correct language and using routine matrices and routine and non-routine matrices and _alogical structure, engineering problems using determinant operations. determinant operations. ‘non-routine matrices, determinant and complex ‘Assessment practice 8.2 Assessment practice 8.2 ‘operations, while solving al the given problems accurately using routine and non-routine operations. ‘Assessment practice 8.2 oarning aim [canine now complex unberscanbe sda ohe Solve given problems using _ Solve given problems accurately using routine complex number routine and non-routine complex number operations. ‘operations. ‘Assossment practice 8.2 ‘Assessment practice 8.2 Learing alm i ovestee how ssl ard probably tgs meets Orchengrecing tems no pa Solve an engineering problem Solve an engineering problem accurately Evaluate the correct synthesis and application Using routine central tendency, using routine and non-routine central —_of statistics and probability to solve engineering. dispersion and probability tendency dispersion and probability problems accurately involving routine and non- distribution operations. distribution operations, providing an routine operations. Assessment practice 83 ‘explanation of the process. ‘Assessment practice 8.3 ‘Assessment practice 8.3 Da Solve an engineering problem Solve engineering problems accurately sing routine linear regression using routine and non-routine regression operations. ‘operations, providing an explanation of ‘Assessment practice 8:3 the process. ‘Assossment practice 8.3328 Getting started You have already studied quite a few mathematical topics, and gained skills and knowledge. Think back to what you have learned in the past. Try doing a few warm-up questions from your previous work. List your mathematical skills and make a truthful estimate of your ability with them, Like all skills, mathematical skills benefit from practice. When you have completed this unit, see how your previous skills and knowledge have developed and identify some new ones to add to your list, A Examine how sequences and series can be used to solve engineering problems A1 Arithmetic and geometric progressions Sequences One way that you can begin to understand the relationship between measured values in an engineering problem isto look for patterns by putting the numbers in sequence. This makes it easier for you to examine how the values relate to each other. You can express the relationship as a rule to identify when values fit into a sequence. n some cases, the rule can be written as an equation Look at the following sequences: > (1,2,3,4, 5}isthe sequence of the frst five positive integers. It could also be called the frst five counting numbers or simply the numbers 1 to 5, Ths sa finite sequence. (Note that more than one rule can describe the same sequence.) > (1,2,3,4,5, -}is a similar sequence, but the three dots "1 indicate that the sequence continues indefinitely, This isan infinite sequence > Assequence does not have to increase. For example, {5.4,3,2, I}is the sequence counting down from § to 1. This is a finite sequence. > Asequence can contain the same number many times. For example, {7, 0, 1.0, 1, .. isan alternating sequence of 15 and 0s. This is an infinite sequence. A sequence isa set, but not all sets are sequences. The examples above highlight two differences: > The elements of a sequence are in order. > Anumber can be repeated in a sequence, butin a set each number can appear only once. Further Engineering Mathematics One famous sequence was described by an Italian known today as Fibonacci in his Book of Calculations. Investigate the Fibonacci sequence. How is it formed? What is the link between numbers in the sequence (called Fibonacci numbers)? Who was Fibonacci? When was he alive? ‘What important system did he introduce to Europe?’ Progressions The Fibonacci sequence is actually a progression because ittmeets the criterion of each element being related to previous elements by the same rule. Each element is the sum of the two previous elements: Np =p ya? ‘The Fibonacci sequence occurs naturally in such examples, as the number of seeds in a seed head and the way a snail shell grows. Look at the patterns made by the petals of a flower. Do they follow a Fibonacci progression? Sequence - a set of numbers written in order according to some rule. Each value in the sequence is called an element, a term ora member. Progression - a sequence in which each term is related to the previous term or terms by a uniform law. All progressions are sequences, but not all sequences are progressions.‘Learning aim A ie) sonewouyeyy Suueu8ug saypang Hl > Fibonacci numbers in nature Series ‘The sum of the n-term sequence {a}, 4,43, as Sy=0) +a, +a;+..44, . For example, the sum of the first four terms in the Fibonacci sequence (1.1,2,3,5,8, 13, is Sp2 141424327 Write the following sequences: a) the first five odd numbers b) the numbers counting down from 50 in fives «) the number of days in each month starting from January d) the square of integer values. 2. Identify which of the above are finite sequences. 3 Identify which are infinite sequences. 4. Identify which are progressions, @EMW heck that you understand the similarities and differences between a sequence and a progression (EMD _Whatis the diference between a finite sequence and an infinite sequence? 1 What is the 20th term of the Fibonacci sequence? (Try to calculate it without writing out all the values) 2. Calculate 5, for the sequence {2, 4, 6, 8, 10, 12, 14, ..). @ PAUSE POINT Arithmetic progressions The sequence in the second ‘Extend’ question ofthe Pause Point above isan example of an arithmetic progression, The common difference between terms is 2. Table 8.1 shows how the numbers in this progression are formed. Series ~ the sum of the terms ina sequence. Arithmetic progression -a > Table 8.1 How the numbers in the progression {2, 4, 6,8, 10,12, 14, . are generated re or rr mn? sequence of numbers where sequence a | the difference between any value [2 (4 [6 8 0 | ‘|t4 || two successive terms isa How formed {2 |2+2|2+(2x2) 2+(2*3)|2+(2x4) 2+(2x5)|2+(2x6)|.. | | constant. This constantis called = = he common differ > The Ist term is a= 2+ (2 (0)) seme cence) > The2ndtermis —— ay=2+(2%(1) > The nth term is a, =2+(2* (n= 1) 329330 For any arithmetic progression, with initial value a and common difference d, the terms are {a,(a + d), (a+ 2d), (a+ 3d), (a+ (n~ Td.) The last term of a finite arithmetic progression is Ja (n—Wd Worked Example An oil rig drills to a depth of 1000 metres. Estimate the cost of driling if the first metre costs £200, with an increase of £22 for each further metre drilled Solution This isan arithmetic progression with 2= 200, d= 22, n= 1000, The cost of driling to a depth of 1000mis the 000th term in the progression: A)q09 = 200 + (22 x (1000 - 1)) = 200 + 21978 = 22178 The costis £22178. Arithmetic series The sum of the first n terms in an arithmetic progression is + (a+ d)+ (a+ 2d) + (a+ 3d) +... (a+ (n- 1}d) This can also be written in two slightly different ways: 3nfa +) where lis the last term in the sum, or Sy=}m(2a + (n= 1)d) Arithmetic series - the sum of the terms in an arithmetic progression. Calculate: 4) the 9th and 17th terms of the arithmetic progression with first term 10 and ‘common difference 4 b) the 12th and 20th terms of the arithmetic progression with first term 60 and common difference ~6 ) the 4th and 10th terms of the arithmetic progression with first term 2 and ‘common difference! @ PAUSE POINT Caleulate: Investigate how you can show thatthe three equations for finding the sum of an arithmetic progression are actualy the same. You can find the proof in many textbooks or on the internet. Worked Example Find the sum of the first 15 odd numbers, Solution Step 1: Identify the first term, the common difference and the number of terms in the sum: a=1d=2n=15. ‘Step 2: Substitute the values into a formula for ,, Using $, = In(2a + (n~ 1)d) directly: Sp = HISN2 «1 + (15 ~ 1) x 2) = 225 ly fist calculate the last term land then Altern: use 5,=4nla+ f J=14(15~ 1)2)=29 S, 15)(1 + 29) = 225, ‘The arithmetic mean is the sum of the arithmetic series, divided by the number of terms Sy arithmetic mean = 7¢ For example, the arithmetic mean of the first 15 odd numbers is: Follow the steps in the worked examples carefully 4) the time taken to make 200 components if the first one takes 5 minutes and each additional one takes 2 minutes b) the sum of the first 20 even numbers. the arithmetic mean of the first 20 even numbers. Further Engineering MathematicsGeometric progressions ‘The geometric progression {I, 3, 9, 27,81, 243, .) has first term a= 1 and common ratio r=3. Geometric progression - 2 In Table 8.2 we look at the numbers in this progression more closely. sequence of numbers where each element is multiplied by Table 8.2 How the numbers inthe progression (1,3, 9, 27,81, 243, .) are formed ean ) a constant value to form the Position in sequence n=4 [n=5 |n=6 |__| next element in the sequence. Value 1 3 9 a a 28 This constant multiplier is, How formed 1 Tas [tase [tx [ae | TH! The mth term is 1 « 3"! In general, you can write a geometric progression with first term a and common ratio r as {a, ar", ar’, ar, .. ar}. You can also have a negative and/or fractional common ratio, Worked Example - Motor jpeedy ‘The motor powering an oil drill has ive speeds. These vary from 10 rpm to 160 rpm in a geometric progression. Find the common ratio, and make a table showing the five required speeds, Solution Extract the data given in the question: a, = 10, a5= 160,10 > Table 8.3 The five speeds of the motor The nth term is given by a, 160 = 10r6" r=VT6=2 Now you can make a table showing the five speeds, as in Table 8. 4, =10% 2° 100rpm a, = 10*2)=200rpm 4, = 10x 2?= 400 rpm aq= 10» 28= 80.0 rpm a5 = 10 2*= 1600 rpm Worked Example — Depreciation. costs {An engineering company installs a new machine for £75000, The machine's value depreciates ata rate d of 15% per annum (a yea). ) What will the machine's value be after seven years? b) How long will it take for the value to be less than £37500 (half the initial value)? Solution 1a) The value of the machine in successive years forms a geometric progression. ‘The initial value is taken to be at year 0: ay = 75000. The common ratio is r= 1 -d= 085. Note that because we start at year 0, the equation for the nth term of the geometric progression (representing the value after n years) will be a, Therefore the value after seven years (r }) will be 5000 x 0.85? = £24 043.28 or £24043 (to the nearest pound) sonewayyey SuueauSug saying 331b) To find how long it will take for the machine's value to equal £37500, solve the equation: 37500 = 75000 (0.85)" Rearrange to make n the subject: 37500 7 ; ; Sro90 7 085) Divide both sides by 75000. log(}} = nlog (0.85) Take logs of both sides and use the rules of logarithms. =0 30103 = n(-0.07058) -0.30103 0.07058 | will take 4.3 years for the machine to depreciate to less than £37500. 265 Geometric series ‘The sum of a geometric series is given by S,eatarsarsar+..rar This can also be written as, 55-8 oie tare Investigate how you can show that the two equations | Worked Example for the geometric series are equivalent Find the sum of the first five terms of the geometric series 1 +3 + 9+ Solution Identify the parameters: Substitute these values into the formula: ai =r) a-9 Vx(1=3) 1-243 242 _ Boia a-3 7-3 2 s, Geometric series thesum |) hi aid santas ofthe terms in a geometric vergence of a geometric sel progression, IF the common ratio of a geometric progression is a proper fraction (either positive or ‘negative, but smaller than 1 in size), then each term will get smaller as n gets bigger. In other words, the terms become less significant the further along the series you go. Convergent series - a series for which 5, heads towards a specific value as n (the For example, ifa= 4 and r= }, the geometric series is number of termsin thesum) | 4+1+1+ increases. Divergent series - a series for which S, does not settle down toa definite value as n Increases. You reach a point where adding more terms does not make any noticeable difference to the total - the series converges to a final value. The sum to infinity of a convergent ite geometric series is prod that ? stands for sun Ue (a+ by Summary - binomial expansions A binomial (a+ by", where m isa positive integer, expands to give terms ina’, a™b!, 2b, a 363 et. The final term is br The sum of the powers in each term equals The coefficient ofthe first and last terms is 1 The coefficient of the second and penultimate termsis n The coefficients can also be obtained using then choose r function, ‘The first term in the expansion has r= 0. ‘The expansion of (a + b)" can be written as nr Ifthe first term in the binomial expression is 1, then we get the simpler formula (eared ems AO MOB This is valid for positive integer values of n, but what about other values? The binomial expansion for (1 + x)" can still be carried out when nis nota positive integer, but only if the value of x lies between -1 and #1. The expansion gives, an infinite series. In applications, you have to decide at ‘what point further terms in the sum become so small as to be insignificant Check the conditions for the binomial expansion of (1 +3)"1to be a convergent Try simple numbers in the binomial expansion. For the following binomial expressions, calculate the values obtained using the binomial expansion formula and check the answers against values given by a infinite series. «xn Gx calculator 1 (+02) aogn 00) 1 =(eay (142) Cie 2H Further Engineering MathematicsLearning aim A Cue} Worked Example You have just built an electronic circuit that gives an oscillating signal. The periodic time of the oscillation is, given by the formula T = 2mvEC, where L and Care the values of the inductor and capacitor in the circuit. ‘When you measure the values used, you find that the inductor value is 2% above the nominal value, and the capacitor value is 1% below its nominal value, Use the binomial expansion to calculate the expected percentage error in T, Solution Step 1: Write the equation for T using the actual values of the inductor and capacitor, which will be 1.02L (2% above nominal value) and 0.9C (1% below nominal value). The measured value of Tis T= 2ny{1.021)(0.99C) Step 2: Rewrite T with the coefficients as binomial terms: T= Amy{(T + 0.02) - 0.07)C) = 2nVLC(I + 0.02)(1 - 0.01) vic + 0:02)/{1 = 0.01) = 2milC( + 0.02)5(1 - 0.01} Step 3: Apply the binomial expansion formula to (1 + 0.02}! and (1 ~ 0.01)! separately (1 +0002)! has x= 0.02 and n= 3 Ble Nagy» BE WO Aoogp (1 + 0,02)? = 1 + (1)(0.02) + 2 = 1 +0.01 - 0.00005 + 0.000005 + .. « 1.00995 (1 -001)thasx=-001 andn = a- 1) aG- WE-3) (1-001) =1+ (3-000) + EN oot oop = 1 ~ 0.005 - 0,0000125 - 0,0000000625 + ..~ 0.99499 Step 4: Calculate the expected error in T (1 + 0.02)%(1 ~ 0.01)! = 1.00995 « 0.99499 = 1.00489 so the expected percentage error in Tis 0.00489 = 0.489%. The binomial expansion of (1 +x)” for all positive integer values of r n(o- 1), nln Tn 2) oe ee ‘The expansion can also be used for values of n that are not positive integers, provided that x lies between ~1 and +1 +e (leayr= Te mee soneuaureyy Suusauiug sony 338 e fa bi c 4)en3x2 maim ci (@ bc d)isat x4 matrix abcde Gants ‘Some matrices have special names: > Ann x1 matrix is called a ‘column’ matrix. > A1xnmatrixis called a tow’ matrix. > Amatrix with an equal number of rows and columns (for example, 2 x 2 or 3 x 3)is said to be square. (G.@ 7) 8a2*3 manic ) 22 5 mati The entries in the matrix (the a, b,c etc, in the examples above) are the elements of the matrix. These are sometimes expressed by their coordinates within the matrix, for example M5) a2 and the second subscript is the column number. (: “) ere the a subst throw number The diagonal from top left to bottom right of a square ‘matrix is called the leading diagonal, A square matrix that has values of 1 on the leading diagonal and all other elements 0 is called an identity 10 0 ‘matrix (or unit matrix). For example, (0 1 0} is the 3 x 3 identity matrix. Oma A null matrix (or zero matrix) is a matrix in which all the elements are zero. A square matrix where all the elements either below or above the diagonal are zero is called a triangular matrix. Forerample(|. 2) at eo below te agonal oti 400 an upper triangular matrix; 7 1 0} has only zeros 9 1 6) above the diagonal, so itis a lower triangular matrix A matrixis transposed when its rows are written as columns and its columns written as rows, for example fa VT og ( ‘ “(5 § Aner tie superset denates ‘transpose’ Matrix calculations You need to follow a number of rules to carry out calculations using matrices. Some of them might appear odd at first, but they are sensible rules once you understand the meaning of a matrix, Further Engineering Mathematics Matrix addition and subtraction Addition and subtraction can only be carried out when the matrices involved are of the same order (thats, they have the same size and shape). This s because corresponding elements in each matrix are combined. For example, if A= (1 2 3)andB=(4 5 6), then AvB=(l44 2+5 3+6)=(5 7 9) Itfollows that A + B and B + A give the same result. In other words,A+B=B+A Note that the resulting matrix is of the same order as the matrices being added. In general abo g hi As = tae flanga=(2 2 akg bth Figure 8.1 Testing whether matrix multiplication is possible 9 (5.8 ante (9) ree pro HA ‘9 ana-(§ 24 (eects y combining each row of A with each column of B (see Figure 8.2),= ire 8.2 To multiply two matrices together, combine each row of the left matrix with a column of the right matrix. » Row 1 of Aand column 1 of B combine to give (ax g)+ (bn) + (cx) =ag + bh ci Row 2 of Aand column 1 of B combine to give (dg) (exh) (fei)=dg + eh +f sotereting 21 macs "8H*4) In this case you cannot find 8 x A (see Figure 8.3). BX Acannot be done 6 0 ee 3) x ‘The middle numbers do not match > Figure 8.3 Why it isnt possible to calculate Bx A Larger matrices can be multiplied by repeating this process for all combinations of a row from the first matrix and a column from the second. For example: on fa bc’ (2 ‘se-f j innit tsetse to mip Aby 8 oe Figure 8.4) ita RODA > Figure 8.4 The product A x B will bea 2 x2 matric Revi looking at the rules @ PAUSE POINT Learning aim B ue) For A x B the element in: > row 1 column 1 results from combining row 1 of the first matrix with column 1 of the second matrix > row 2column 7 results from combining row 2 of the first matrix with column 1 of the second matrix, > row 1 column 2 results from combining row 1 of the first matrix with column 2 of the second matrix > row 2 column 2 results from combining row 2 of the first matrix with column 2 of the second matrix, The products A (ae ahs bj+el dg+ei+fk dh+ej+fl Writing equations in matrix form ‘Suppose that, in analysing an electrical circuit, you had this pair of simultaneous equations: 2h +3l=12 @ 3h + 4h =8 @ You could wie them in maticormas (2 3\fh\_ 12) (3 aQ)-(3) The genera mata for ofa sto smutaneous tina wioens Ake¥ In this example: > v2(2)-the column maticofvaeson height hands tthe egal the rules for combining matrices, then answer these questions without 1. What size does a matrix need to be if you want to add itto a2 x 4 matrix? What size will the resulting matrix in question 1 be? 2 3. How would you multiply a matrix by 5? 4. How would you divide a matrix by 5? 5 a) Can you find the product AB if Ais a2 3 matrix and B is a3 x5 matrix? +) Ifyou can, what will be the size of the resulting matrix? )In this case can you find the product BA? If not, explain why. 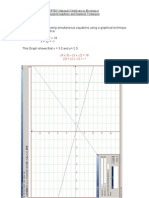a rTSolving simultaneous equations by Gaussian elimination You have probably used elimination and substitution methods to solve simultaneous equations. One of the difficulties you might have encountered is that each pair of equations may be solved in a different way, depending on the values in the equations Gaussian elimination provides you with a standard procedure that can be applied to any set of simultaneous linear equations, The procedure is as follows. Step 1: Create an augmented matrix of numbers from A and ¥. Step 2: Create a triangular matrix by successively eliminating variables so that only ‘one variable remains in the bottom row, one more variable in the row above, and so on up to the top row where all the variables remain. Step 3: Read off the value of the variable in the bottom row. Step i Substitute its value into the row above, which then allows you to calculate the value of the second variable. Continue substituting the values of the variables you have found into the row above, until you have reached the top row and found them all |n the two-equation example above, the 3 in the lower left comer has to be » Figure 8.5 Augmented matisfor converted toa zero first, which eliminates its variable (1) in thet row (see Figure 8.5). applying Gaussian elimination to the system At this stage you only need to know how to solve problems with two variables. Worked Example Solve these we simultaneous equations using Gaussian elimination Bx+2y=-3 (1) Sx 3y=-4 2) Solution Stop Witte settequatonsinmatixfrm axe yso(2 2) : and ¥ into an augmented matrix: (3 2-3) Step2: Merge and Yinto an augmented matrix (32 | 3) Step3: Theaimstogetazeoin pace ofthe sleet in thelower econ Tooth. st mlipy row by and ow 2b 3 (3x5 2x5]-35)_/15 10 3) Ges sa3[cc)-(i3 3/3 Then subtract row 2 from row 1 to get (01-3) Repcethe scontowintheaugmend maencwintieenewvaies(3 23) | Step: Conver his augmented equation bucktosmutanceus equations segs) Ox + Iy=-3 @) Step 5: Equation (3) has no x variable and gives y = -3, 40 Further Engineering MathematicsLearning aim B SUT: Step 6: Substitute this value of y into equation (1) 3x+2(-3)=-3 3x-6=-3 xel The solution is x= 1 and y=-3. Check the answer by substituting these values back into the original equations: 3(0) + 2-3) 5(0) + 363) So the solution is correct. sonewauzeyy SueouSug saying Write this pair of simultaneous equations in matrix form: @ PAUSE POINT Bx+2y=2 axty=4 EMD Follow the worked example carefully. (QQ _ Solve the simultaneous equations by Gaussian elimination, A square matrix that does not have an inverse is called a B2 Determinants is singular matrix, The determinant ofa singular matrix is 0 Determinant of a 2 x 2 matrix The determinant of a matrix A can be written in a number of ways. The most common forms are det(A) or |A) Determinant - a useful value calculated from the elements of a square matrix. You can calculate the determinant of a 2 «2 matrix using a simple formula de® 8) =f Yo atte Worked Example in minantof(1 2 Find the determinant of (} 2) Inverse of a matrix ~ a matrix which when multiplied by the original matrix gives the identity (unity) matrix. Unity matrix ~ a matrix with a1 in each position in the leading diagonal and 0 in every other position. Worked Example Find the inverse of. Solution als 2) 4 Inverse of a 2 x 2 matrix You can use the determinant of a square matrix to find the inverse of the matrix, ab) 2») he inverseis given by (1 2) \3 4) (1x4) =(2%3)=4-6 For a2 x 2 matrix. Solving two simultaneous equations using sila -b maqlS a) Because all elements ofthe matrix need to be divided by A. ifthe determinants zero then the inverse is undefined the inverse matrix You have already seen that the matrix form of aset of simultaneous equations is AX = ¥, where Xis the column matrix of variables. Therefore the solution to the problem 4should be of the form X-= .. which means that we need to rewrite the equation AX = Yto make X the subject. To do this, we would have to ‘divide both sides by A, but there's a slight problem - division by a matrixis not yet defined, We get around this by multiplying both sides of the equation by the inverse of A ATAK=AqY The inverse A cancels out’ the matrix A, so we get X=Aqy Worked Example Use an inverse matrix to find the solution to these simultaneous equations considered in an earlier worked example: 3x4 2y=-3 0 5x+3y=-4 @ Solution Step 1: Write the equations in matrix form as & 3)0)-(3) Step 2: Calculate the determinant of A= ( 53 Step 3: Use the formula for A": 5G 3)-(2 3) Step 4: Calculate X= A (2 3NC) First, check if the multiplication is possible. ‘The matrices being multiplied are 2 x 2and 21 The middle numbers agree, so you can multiply, ‘Combine each row of A with the column matrix ¥: . (ongaczrea) (4) 3 3) #8 x 3)-(2 « 9)=9-102-1 5 x (-B) + [-3) x (4) So the solution to the simultaneous equations is x= land y=-3, This agrees with the answer obtained using Gaussian elimination, Further Engineering Mathematics Determinant of a 3 «3 matrix You can find the determinant of a 3 x 3 matrix by using the values in the first row and their minors, The minor of a ‘matrix element is the determinant of the smaller matrix left ‘when you cover up the row and column of that element (see Figure 8.6). +ife rf) — ja fl + lae ts at gh ‘st term 2nd term 3rd term > Figure 8.6 Using minors of a3 x 3 matrix to find its determinant b fe Hands TT g For A Worked Example A system of ropes and pulleys has three ropes Under tension, The tension in each rope satisfies these equations: M+h-4h=2 (1) Bh +h=6 Q AT, + 6T,=1 6) Find the determinant of the coefficient matrix, Solution ‘n matrix format the system of equations is 21 -a(h) 72 ( 1 2} -(8} 0 -4 6A) Mi 21 Thecctcen macea (3 1 ) 0-4 6 1 B O48 7 adh deem 2 (1 * 6 0x (-4) ~1(3 x6 - 0x0) + (48 x (-4)-1 x0) Then al = 12-18 +48 = 42 Cramer's rule ‘Cramer's rule isa way of solving multiple simultaneous ‘equations using determinants. Consider this pair of simultaneous equations:‘Learning aim B ST fay by\pxy _ [e1) (2 2)6)-() Make three determinants: 6 ler | al pis pis bd Pil ker bd (Pal I a _ Dl [0.1 Then the solution is given by x= Dp and D provided that IDI is not equal to zero. Worked Example Find he currents j and isn the cc shown in igure 87. Solution Using Kichffs curentue, the ret 1o0R 120k gives the equations 300i, - 2001 200), «320 > Figure 8:7 Circuit diagram Step 1: Write the equations in matrix form (300-20 (' “(23 \-200 320) \in] “ \-20, Step 2: To apply Cramer's rule, form and calculate three determinants, 300-200) ~ €200) x (-200)= . . 390 “ga0|= 300 * 320 ~ (-200) x (-200) = 96000 - 40.000 = 56000 10 -200| - 10 x 320 ~(-200) x (-20) = 3200 - 4000 = -800 il=L29 320 | 30010) 300 x (20) - 10 (200) = -6000 + 2000 ~ [pd=[ 209 12300 (20) 10 (-200)= 6000 +2000 « 4000 step 3: Find i andi [Pil __-800 [Dx j= Dil, =800 9014003 dp) and i= Tor” 56000 * COA lt 34) anda py “The negative answers mean that the current flows in the opposite direction to the one chosen (that is, the current flows anti-clockwise). -0071A (to 3 dp). sonewourew Suesuidia sauna 34ons in matrix form AX = ¥. @ PAUSE POINT — ® Wiiteths pairofsimuitaneous eq 21)+3T,=11 Ti-2T =2 b) Calculate the determinant of matrix A, [Al and its inverse, A’, EMD Use the worked examples to help you answer the questions. Try to repeat the steps of the solutions without looking at the examples. Solve the simultaneous equations using the inverse matrix and 8 Compare the two methods. 1g Cramer's rule, sessment practice 8.2 ue Use these matrices to answer questions 1-3 below. GK 2) + What techniques will need to use to a) ‘complete the task? How am | going to 3) approach each problem and keep track of my 3 progress? + How confident do | feelin my abilities to ‘complete this task? ( 6 ;) + Ate there any areas | think | may struggle o-(-3 21 with? 10 0) Do Fea 3 2) + Lknow what strategies | could employ for the 1. Find the value of each matrix expression. Give a reason if task. Ican determine whether these are right the operation is not possible. for the task. a) A+B b) B+A 9 2B + I can assess whether my approach is working d) AC ¢) DE #) €D and, if not, what changes I need to make. + I-can identify when I've gone wrong and 2 Calculate th inant of: eee adjust my thinking/approach to get myself oe Oe 10 back on course. 3 Calculate the inverse of: eevee ae Di) ae + [can evaluate whether | have solved each 4. The following equations were obtained by applying problem correctly Kirchhoff’s current rule to a circuit: * Ihave compared the different methods and Tis 93 can assess which method is more suitable for which type of problem. eral + Ian identify the elements in the task that where i and i represent the currents in separate branches are difficult for me and explain how | would Find the values of i and izusing approach them differently next time. a) Gaussian elimination b) the inverse matrix method ) Cramer's rule, 5 Use matrix and determinant methods to solve these simultaneous equations describing a mechanical system 27 +3%-Ty=53 T-21)+3T,=16 Tht Ty=27 Compare the answers and the methods 44 Further Engineering MathematicsLearning aim C uy (e, Examine how complex numbers can be used to solve engineering problems C1 Complex numbers Complex number - a riumber that has the format Complex numbers extend the range of numbers from positive and negative values + jb, The ‘complex operator’ con the number line to two dimensions. Any complex number can be written as.@jb, | or imaginary unit’j satisfies where ais the horizontal component along the familiar number line (called the the equation j2= -1 real part) and b is the vertical component along a perpendicular direction (called the imaginary part). The symbol indicates the imaginary’ component. (Note mathematicians use for the imaginary unit, but engineers use j' to avoid confusion with the symbol for electric current) : z 4 345 Phasors are discussed in Complex numbers make it convenient to perform mathematical operations with Unit 1, in the sections phasor quantities. A phasor isa rotating vector. The instantaneous value of a sine ‘A2 Trigonometric wave at any point is equal to the vertical distance from the tip ofthe phasor to the methods’ and‘G Single- horizontal axis (see Figure 8.8). phase alternating current’ 180° / ns my 319 40, > Figure 8.8 Relationship between a phasor (rotating vector) and a sine wave ‘Aphasor that starts at the 3 o'clock position and rotates anti-clockwise represents the sine wave y = Rsin(wt), where R is the length of the phasor and w = 2nf(rads”) is the angular speed (here fis the frequency of the sine wave oscillation in units of Hz). A phasor that starts at the 12 o'clock position represents the function y = Rcos(tl, where R and w have the same meanings as above Because 90° is radians, you can see that R cos ith = Rsin(ist + 2 Look at the two waves A and B and their phasor representations in Figure 8.9.») 30° 180% O° 270° > Figure 8.9) Wave Bisa phase-shited version of the sine ‘wave A. (6) The corresponding phasor 8 makes an angle of 30° with phasor A In Figure 8.9 the phasor B leads the phasor A by 30", 0 radians. We know the equation for Aisy = Rsin it Th 1 Bisy = Rsin(ut + equation for Bisy = Rsinut +2) A phasor can be written in a number of ways. The most ‘common forms are the following > polar notation - where the magnitude (also called the modulus) R and the phase angle (also called the argument) are together expressed as R20 > rectangular (or Cartesian) notation - where the phasor is resolved into horizontal (a) and vertical (b) components to give a + jb. Figure 8.10 shows how to convert between these two. forms of notation, Figure 8.10 Conversion between polar and rectangular forms of representing a phasor Further Engineering Mathematics In particular phasor with rectangular form a+ jb has > modulus|a jbl = va? eB? bY > argument argia + jb) = tan-i(2) The complex number system lets you add, subtract, multiply and divide phasor quantities that have both magnitude and angle (see the section on complex number arithmetic below). Numbers on the complex plane If you plot complex numbers on a set of perpendicular axes (the complex plane), you get an Argand diagram (sce Figure 8.17, 444 Polar notation > Figure 8.11 Two examples of Argand diagrams The j operator is associated with the vertical component of the phasor. It represents an anti-clockwise phase shift of 90° or rad. A shift followed by another j shit gives? Which is equivalent to a 180° phase shift, This corresponds to the wave being inverted, or multiplied by ~1. Therefore j satisfies the equation jComplex number arithmetic Addition and subtraction You add (or subtract) the ‘real’ and ‘imaginary’ parts of an imaginary number separately. For example: (2 +3) + (4+ 5) =(24 4) + (3 +58) =6 +58 (1 =)2)- (8+ j4) =(1 ~3) + (i2-ja)=-2-j6 Multi You can multiply in rectangular notation the same way as. ‘multiplying two binomial terms, using FOIL. For example: (2+ j3[4 +} ication + flO +j12-+)215 = 8+ 22 +j215 But you know that ? = -1, so the last term becomes ~15. Therefore (2+ jaa +) 4 j224j215 =84j22-15 =-7+j22 You can also multiply two complex numbers in polar notation. To do this, multiply the magnitudes and add the phase angles. For example: 2+)3=V18 {tan} rad {an a cian) ra aaj So (2 +J3)4 + 5)=013V4T z(tan-13 + tan) = 23:09 21.8788 rad Converting this back to rectangular notation (using unrounded values) gives 23.09 cos(1.8788) + j 23.09sin(1.8788) = -7 + j22 Division To divide two complex numbers in rectangular notation, you write the division as a fraction and then multiply both ‘numerator and denominator by the complex conjugate of the denominator, ‘A complex number and its complex conjugate have the same real and imaginary parts, except that the j terms have opposite signs. In other words, a+ jb and a - jb are complex conjugates of each other. Multiplying a pair of complex conjugates gives areal number: a + jbfa ~ j= a2 jab + jba~ j2b? =a +b? For example, to divide (2 + j3) by (4 +j5) using complex conjugates 2+i3)_2+33!4-J9)_ 8 (4+15) (4 +)5\ ° 8+j2+15_23+j2 232 “esas aT an aT You can also divide in polar notation: simply divide the magnitudes and subtract the phase angles. ‘Learning aim C De} G W3e(tan*3 Fad) vare(tao5 | = 0.56320.0867 rad Converting this back to rectangular notation (using. unrounded values) gives 23) 9563 cos0.08671 + snf0.0867) +5) = 0556 + 0.05 (to 2 dp) Most scientific calculators have polar-to-rectangular and rectangular-to-polar conversion functions. Find out how to carry out these functions on your calculator, and practise using them, Raising to a power Raising a complex number to a power m is easy to do in polar notation using De Moivre's theorem: (R20)"= Reznd In other words, raise the magnitude to the power n and ‘multiply the phase angle by n. Worked Example An electrical circuit has an inductive reactance of 8 +4}. connected in series with a capacitive reactance of 0-2) anda resistor of (15 +) Calculate te total impedance and the current flowing inthe creut the voltages V= 122 Fad Solution The total impedance is Z= 3+ j4)+ 0-2} + (15 +) = (18 + j2}22. The current in the circuit is ind To do the division, you can convert Zto polar notation: 2) 22219892 a(tan-? 18-2216 c{tn2) =18.1120.1107 rad ee oy iain?" 7a = 0663209365 rad ‘The currentis 0.663A ata phase angle of 09365rad This eam also be written asi = 0663 sn at + 0.9365) 4-0m007) sonewouzey Suveouaug seyung 347‘Answer the following questions involving complex numbers. Itis pla. important that you show all the steps in your calculations clearly i Wihiancechniqués wilfinced use 9 You also need to give a brief explanation of each step. 1. Youare given the complex numbers 2\=34jandz=4-j a) Plot z, and z) on an Argand diagram, ») Calculate the following i) thesumz) +z, ii) the conjugate of z il) the conjugate of z iv) the product 212» in rectangular form V2, and 2, in potar form vi) the product 2,2: in polar form i) (z2)in polar form using De Moivre's theorem viii) (2,P in polar form using De Moivre's theorem complete the task? How am | going to approach each problem and keep track of my progress? + How confident do | feelin my abilities to complete this task? + Are there any areas | think | may struggle with? Do + know what strategies I could employ for the task. can determine whether these are right for the task + Ian assess whether my approach is working and, if not, what changes I need to make, + [can identify when I've gone wrong and adjust my thinking/approach to get myself back on course. Review + I can evaluate whether | have solved each problem correctly. + Thave compared the different methods and Zz ix) the quotient 3 in rectangular form 4 z 8h x) the quotient z in polar form. 2. Two circuits are connected in series. The impedances of the circuits are z; = 50 + j3 and z; = 20 ~ j2, and the supply voltage is v = 100 + §j aerial ' can assess which method is more suitable |) the total impedance zy =z; + 2, y for which type of problem. i)_the current flowing inthe circuit, = + Ican identify the elements in the task that b) What is the amplitude of the current? ©). What is the phase angle of the current? are difficult for me and explain how | would approach them differently next time. Investigate how statistical and probability techniques can be used to solve engineering problems D1 Statistical techniques Data can be gathered from many sources. It can be classified as diserete or continuous. Probability distribution ~The distribution of values of a variable can be displayed graphically, eg. as a histogram or pie-chart. A probability distribution plots the probability of a given value against the range of values instead of the actual number. A very common distribution is known as the normal distribution. A normal distribution gives a bell- shaped curve, symmetrical about the mean. > Data is said to be discrete if it can take on values from a specific set of numbers. For example: + The number of people living in a house can be 0, 1, 2, 3, .. But not, say, 24 oF 35. + The number of cars produced in a factory in a week must be a positive whole number or zero. > Data is said to be continuous ifit can take on any value within a range. Continuous data usually comes from measurements. Examples include ‘ the diameter of a spindle turned on a lathe + the volume of liquid in a container. 348 Further Engineering MathematicsMeasures of central tendency (averages) ‘When you analyse experimental data, its useful to look for a single number that typifies the data - the average value of the data. There are three important averages that are often used > arithmetic mean - defined as sum of all the data values number of data items in the sample Us expressed mathematically as ¥ == > median - the middle value of the data when all the values are placed in order from lowest to highest. To find the middle position, add 1 to the number of data items in the sample and divide by 2. > mode - the data value that occurs most often. f more than one value occurs the same number of times, the datas said to be multi-modal This can be Raw data is ungrouped. For example, ifthe number of components produced per hour is measured over ten hours and recorded as 10, 11,10, 9, 12, 11,10, 10, 9,11, this is ungrouped data. This small amount of data can be analysed quite simply: mean - 1011 eile meri NOaTOESeTY . To find the median, first write the numbers in order: 9,9, 10, 10, 10, 10, 11, 11,11, 12 In this case the median is halfway between the fifth and sixth values, These numbers are both 10, so the median is 10. To find the mode, tally the values as in Table 8.4. 0.3 Tally chart to make a frequency table Tally | Frequency la 2 ML 4 | nh UE 3 | i 0 1 | ‘The value 10 occurs most frequently, so the mode is 10. Tallying the data when itis collected can make analysis simpler, especially for large sets of data. The data in the tally chart is already ordered, which also helps in identifying the median. Graphical representation of data Tables of data contain numerical values, but patterns and relationships are not always easy to find. Graphical and other visual methods allow you to see potential patterns without the need for calculations. ‘Learning aim D SUT} A pie chart (Figure 8.12a) isa useful way of comparing relative sizes of data in specific categories, for example, the number of different types of industry in an area, A bar chart (Figure 8.12b) is an alternative way of displaying values of similar types of data to pie charts. A histogram looks similar to a bar chart, buts used for displaying the frequency of grouped data. It displays the spread of values, for example, the number of components within a range of measured values (see the worked example below). a “Types of Engineering industry Process , Engineering _tlectronic Tae Engineering 15% Electrical Engineering 1% Light Heavy Engineering Engineering 45% % b) ‘Types of Engineering Industry 8.10. é g 5 2 vi 8 ,F gf gt 52 23 32 =: 83 > Figure 8.12 Graphical representations of data: a) a pie chart, ‘and b)a bar chart Revise the different ways of representing data as + pie charts + barcharts + histograms + cumulative frequency diagrams. Make sure you understand the difference between bar charts and histograms. soneweureyy SuysaurSug saying 349Worked Example Consider the data presented above: 10,11, 10, 9, 12, 1, 10, 10, 9, 11 Calculate the mean of the data using a frequency table. Solution > Table 8.5 Frequency table The means x f ot «+ fisthe frequency of each di ° 2 ue + Ef Nis the number of data items in the sample Dy wD + xfisthe contribution of each value x to the total i 8 ® + fis the sum of all the contributions, that is, the total ofall the v ‘ iV data values, Dfe10 — xf=1083 Tabulate these values as in Table 8.5, and then use the formula to Meng =2% _i93 calculate the mean bi Grouped data Larger sets of data are more easily analysed if they are grouped Classes - the groups into which the data is organised, Lower class boundary (Icb) - the lowest value ofthe class. Upper class boundary (ucb) - the highest value of the class. Class width - the difference between ucb and Icb. Midpoint - median of the class. Worked Example ‘A machine is set to produce bolts with nominal diameter 25.00rmm. A random sample of 60 bolts is measured and provides the frequency distribution in Table 8.6. a) Calculate the mean diameter, ) Drawa histogram of the data and mark the upper and lower class boundaries for the second class. > Table 8.6 Frequency distribution of bolt diameter Diameter(x) Frequency (f) 233-287 2 238-242 4 243-287 10 248-252 v 253-257 16 258-262 8 263-267 3 350 Further Engineering MathematicsLearning aimb = UN Solution 4) The data is continuous. Expand the frequency table to show the Ic, ucb and midpoint of each class (see Table 8.7). Note that the ucb of the first class isthe Icb ofthe second class, and so on. Averaging the Icb and ucb for each class gives the midpoint of that class The midpoint will be used to represent each class in the calculation of the mean. > Table 8.7 Calculation of the mean using the midpoint values soneweyieyy Suuodui8ug soyung Diameter, x Frequency, f = Ieb_ uch Midpoint, Xnig Xiah nen 2 2325 2395 2350 a em 4 2375 aa 2400 96 3247 10 2428 2475 uso as me252 017 2475 2525 2500 25 253-257 16 2525 25.75 2550 408 282628 2535 2625 2600 208 263-2673 2625 2675 2650 795 sy-60 yf 15085, : Da Mean ¥ oo sasta ‘The mean diameter of the bolts is 25.14 mm. ) Using the information in Table 8.7, plot a histogram as in Figure 8.13, Frequency 73.50 24.00 24.50 25.00 25.50 26.00 26.50 Radius > Figure 8.13 Histogram ofthe bolt diameter data ‘A cumulative frequency graph shows the cumulative total frequency up to each of the class boundaries. For example, Table 8.8 shows grouped data on the marks gained ina mathematics test. > Table 8.8 Frequency table for marks gained in a mathematics test | Marks [Number of learners frequency) | Curmulative frequency [n-20 |2 a [2 [2 (2130 a - ize B fae 49 —13+19 32 41-50 36 32036 | 68 | 51-60 42 68+42 | 0 61-70 31 To+31 141 ne vies 154 ‘ss 6 [sa+6 160 | 351352 ‘The cumulative frequency graph is shown in Figure 8.14. At each ucb value along the horizontal axis, the cumulative frequency up to that point is plotted on the vertical axis. 40 $0 6070 Inter-quantile range > Figure 8.14 Cumulative frequency graph of the mathematics test marks Because the final cumulative frequency value is 160, the total number of learners who took the test was 160, So if all the marks were ordered from lowest to highest, the ‘median mark would be around the 80th value. To obtain the median mark from the ‘cumulative frequency graph, find 80 on the vertical axis, draw a horizontal ine across to the curve followed by a vertical line down to the horizontal axis, and then read off the value on the horizontal axis. The lower quartile is one-quarter of the way up the ordered lst of marks (around the 40th), and the upper quartile is three-quarters of the way up (around the 120th). The inter-quartile range isthe difference between the upper and lower quartiles and gives a measure of the spread of data values. The frequency scale can be split up in other ways than into quartiles. For example, ‘the range can be divided into 100 equal steps called percentiles, These can be used to ‘ealculate the inter-percentile range. The range between the 7Sth and 100th percentiles is equivalent to the upper quartile Measures of dispersion (spread) if you were manufacturing components, ideally you would want them all to be the same. You know, however, that there will always 3-2-1 ~0~ OT ‘Mean Standard deviation be some variation. The variation is likely to follow a ‘normal’ or ‘bell- curve’ distribution about the mean (see Figure 8.15). Many things follow a normal distribution, for example, heights of people. |The average variation from the mean will be zero, because in general you expect there to be as many values above the mean as there are below it. You can calculate a useful measure of the variation by first squaring ll the differences from the mean to make the values positive, and then averaging them. The resulting value is called the variance: 2-377 The square root ofthe variance is called the standard deviation, itis usually written as o (lower-case Greek letter sigma), standard deviation = ¢ = Wariance > Figure 8.15 Standard normal deviation 7 Further Engineering MathematicsLearning aim D Worked Example Calculate the variance and standard deviation of the bolt diameters in the previous worked example. Solution Step 1: Calculate the mean. In the previous worked example you found this to be 25.14 mm. Step 2: For each data value (the midpoint of each class inthis case), calculate its deviation from the mean, (~ x). Then square each answer to get ® - x} Step 3: To find the average of these values (x ~ x}?, multiply each one by the corresponding frequency. ‘The calculation results from steps 2 and 3 are summarised in Table 8.9, Table 8.9 Expanded frequency table for calculating the variance Diameter, x Frequency, f Xwig=%; R-*) R= MY R-XPF 233-237 2 2350 642.6896 5.3792 23822 4 240011412996 5.1984 243-247 10 2450 064 ©=—0.4096. 4.036 28282 17 2500 014 = 0196-03332 253-257 16 2550-036 01296-20736 258-2628 2600-086 © 07396. 5.9168 263-2673 2650-136 18496 5.5488 Step 5: Take the square root to find the standard deviation: = Warlance = 0.6898 Scatter diagrams A.scatter diagram (XY plot) is used to visualise the relationship between two sets of data. The independent variable is plotted on the horizontal (X) axis, and the dependent variable on the vertical (Y) axis (see Figure 8.16). = 250 = E200 Investigate probability g 150 distributions, and in particular Z 100 the ‘norma’ distribution. 2 50 Find out how the standard 00 normal distribution curve ole tote 228 288 can be used to predict the Force (kN) percentage of population in a > Figure 8.16 Scatter diagram given range. ll Slee By 353354 In this case the plotted points appear to show that the extension increases as the applied force increases. However, you can see that the points do not fit exactly on a straight line, but the values are scattered closely about cone, with some further away from the straight line than others. Linear regression (line of best fit) When you take measurements, there is always a degree of tolerance. This means that in a practical situation involving measurements of two variables (one independent and one dependent), even when the dependent variable is known to be directly proportional to the independent variable, its unlikely that the data points, willie exactly on a straight line. If you expect a linear relationship between the variables, you could plot the data points and try to draw a line ‘by eye’ that best describes the relationship - for example, you could draw a line that has as many data points below as above it. ‘An alternative to such a ‘it-or-miss' method of fitting data is to use a statistical analysis tool. The linear regression ‘model generates an equation of the form y=mx-+ cto fit the data. The values of m and c are given by Nay -ExZy m= OP AXEY and c NZL where Nis the number of pairs of measurements, is the mean of the data values for the dependent variable and Xs the mean of the data values for the independent variable. - mx statistical quantity that measures how well the regression line fits the data is the (Pearson's) correlation coefficient. This is given by the formula NYxy -Exdy WE x? (Ea? INDY (CoP and produces a value between ~1 and +1 that indicates the degree of correlation between the variables: +1 means total positive correlation, 0 means no cortelation and -1 ‘means total negative correlation, Linear regression is a very useful too! to determine a relationship between the variables. However, not all relationships are linear. You can use a spreadsheet, such as Microsoft” Excel to investigate other potential relationships that fit the plotted points, such as exponential, logarithmic tc, see Figure 8.17) Further Engineering Mathematics > Figure 8.17 Usinga spreadsheet to plot regression lines, The data in Figure 8.17 represents an experiment to relate the rotational energy in a flywheel to its angular velocity. Theory says that the relationship is E= }/w,A linear trendline clearly does not match the data as you might, expect. The polynomial trendline gives a much better fit. The spreadsheet displays the equation of the regression line and the R-squared value that gives a measure of how Well the data fits the mathematical model (equation). ‘Avalue of 1 isa perfect fit. The regression line is close, but, does not quite match the theoretical value. The benefit of Using a software application is that other types of trendline can easily be tried to find a line of best fit Most graphical calculators and spreadsheet programs can calculate the linear regression line and the correlation coefficient. Figure 8.18 shows the regression line calculated for the worked example data using Microsoft” Excel ——s 250} y = 0.7996x +.0.8726 | R5 09778 Le 0, 00 50 100 180 200 280 300° > Figure 8.18 Calculated regression line for sample data, Investigate how to use your graphical calculator or spreadsheet such as Microsoft” Excel to find the regression line and correlation coefficient for a set of dataWorked Example The data in Table 8.10 was obtained during a tensile test ofa steel specimen. The values are plotted as a scatter diagram in Figure 8.16. Assuming a linear relationship, determine the regression line of extension oon force and calculate the regression coefficient, explaining what the value means Solution Make a table (like Table 8.11) to calculate each of the terms in the regression line formulae, > Table 8.11 Table for calculating the regression line Tension (KN) Extension (mm) x yo ox y 9 45 38 2025 144 m7 90 29 e100 79.21 01 130 104 69000161352 180 160 32400 25600 2a 220 196 48400 «38476 = a2 270 73 7900-45369 S751 Bx=935 — Sy=80 Tek= 180725 y= 129566. Tay = 15267 Now apply the formulae for the regression line: NYxy- LXLy_ 6115267) - (93.5)80.0) NDX-(DaP 61180725) (93. = 0.7996 Statistical investigation Inspection and quality assurance, calculation of central tendencies and dispersion, forecasting, reliability estimates for components and systems, customer behaviour, condition monitoring and product performance are all examples of engineering applications that rely upon the application of statistical techniques. The best way to understand them is to carry out a statistical investigation of your own, ‘A common approach to carrying out a statistical investigation follows the Problem-Plan-Data-Analysis~ Conclusion (PPDAC) cycle. Problem: In the problem stage you need to formulate the question to be answered, identifying what data to collect, why itis important, where and how to collect it. ‘Learning aim D Te > Table 8.10 Measurements of tension and extension ina tensile test Tension (kN) Extension (mm) 45 38 90 89 130 104 180 160 20 196 20 23 Dx _935_ 25% 235.215.5853 Zy_200_ Ah 809.1333 = mx = 13.333 ~(0.7996K15.583) = 0.873 So the equation of the regression line is y = 0.8 + 087. The regression coefficient is NY ay- Exdy Dx -TDP WEY (ey 6(1526.7) - 193.5180.0) 1807.3) - 3.5)" Y6I1295:7)- 60.0 This is a positive value close to 1, so there is strong positive correlation between the two variables and the linear regression equation is a good fit to the data. Plan: In the plan stage you identify details such as the sample size, haw the data is to be gathered and recorded. Data: The data stage is concerned with how you organise and manage the data. Tables and tally sheets are typical tools for clearly recording data so It can be manipulated ‘Analysis: Inthe analysis stage you explore the data, looking for relationships in grouped/ungrouped data, using graphical and analytical methods to identify central tendencies, dispersion (spread) and rogue values. Conclusions: The conclusions should relate back to the initial problem. You need to include statistical vocabulary where appropriate, for example, scatter plot, histogram, mean and standard deviation. crm SHNRURIA UOT) 355356 Assessment practice 8.4 Solve the following problems involving statistical and probability techniques. Plan itis important that you show all the steps in your calculations clearly. You also + What techniques will need need to give a brief explanation of each step. nastea'ta Comedie aa 1 You measured the masses of 50 metal castings in kilograms and noted the How am | going to approach results: ‘each problem and keep track 46 47 45 46 47 44 48 43 42 48 of my progress? 47 45 47 44 45 45 46 44 46 46 + How confident do | feel in my 48 43 48 45 45 46 46 47 46 47 abilities to complete this task? 44 46 45 44 43 47 47 46 46 48 + Are there any areas | think | 49 44 45 47 44 45 49 47 45 46 pe i do + know what strategies | could employ for the task. | can )_ Draw the frequency histogram. determine whether these are 4) Is the data normally distributed? right for the task. €) Calculate the mean and standard deviation of the masses. +, can assess whether my, approach is working and, if f) Calculate the upper and lower quartile values. moe eta hanges ead td a) Arrange the data in eight equal classes between 4.2 and 49 kilograms. b) Determine the frequency distribution 8) Calculate the inter quartile range. make. 2. The data in Table 8.12 results from an experiment you carried out to + Van identify when Ive determine the relationship between frequency and the inductive reactance one wrong and adjust my for an electrical circuit, thinking/approach to get ‘myself back on course. > Table 8.12 Data on frequency and inductive reactance iu Frequency, 7 + can evaluate whether | fez) | |° |? bs |» [= [» |= [e[ have solved each problem Inductive | correctly. reactance, |30 |65 |90 | 130| 150] 190| 200 | 255 | 270 + Ihave compared the different x(a) methods and can assess a) Drawa scatter graph for this data which method is more b) What does the scatter graph tell you? sane for which type of 6) Estimate the inductive reactance fora frequency of32kHzfrom the gr@ph. can identify the elements in 4) Calculate the ine of regression of inductive reactance on frequency (yon 3. the task that are difficult for €} Calculate the regression coefficient. me and explain how | would f) What does the regression coefficient indicate? approach them differently next time. 8) Use the equation for the line of regression to predict the inductive reactance for a frequency of 32kHz. h) Compare the calculated value with the value that you read from the graph, Further reading and resources Websites “Maths is Fun: www.mathsisfun.com A lot of useful skills and knowledge organised into categories that are easy to find. mathcentre: www.mathcentre.ac.uk/students/topics A set of resources split into topics designed to support self study. Further Engineering MathematicsUNIT 8 ve been working inthe engineering industry for 29 years, Throughout this time the { Shaun Spilsbury q| industry has never stood still and it continues to develop new technologies across all | s | engineering sectors. believe that design is atthe heart of all engineering Design engineer [A design engineer realises ideas and brings to life new products or processes, from customer requirements, through concept, prototype, nal design and tests to | manufacture: commision and disposal Matheratial modeling and simulation are | Important ways of testing out new ideas before constructing expensive projects, othe | design engineer has to have well-developed mathematical sils The design engineer NK UTURE plays a pivotal role in an extremely diverse range of industries. You have many different ‘and interesting sectors to choose from - including mechanical, electrical and electronic, ‘aerospace, marine, oil and gas, nuclear and renewables (such as wind turbines, solar power) - and new areas are developing all the time. ‘One thing is for sure - it's important to look for a company and position where you will continue to learn and be challenged in an environment that supports your development. Inengineering, every day isa school day and rarely are two days the same, Working ina challenging environment will not only keep you interested while developing your knowledge and competencies, but also be extremely rewarding both professionally and financially. Engineers are sought after the world over, and if you have a desire to workin different parts of the world, then working in this industry provides plenty of opportunities. When working in engineering design, you will be participating in an industry that is shaping the world we live in Focusing your skills Using mathematical skills to solve engineering problems Itisimportant to be able to apply mathematical methods to solve engineering problems. Here ae some simple tips to help you do this Gather al the information you canto understand the nature of the problem ~ fo example, inspection and quality assurance calculation of central tendencies and dispersion, forecasting, eliablty estimates for components and systems, customer behaviour, condition monitoring and product performance. + Use ctl thinking when extracting information from the text ofthe problem, Identify appropriate mathematical methods to solve the given engineerin problem. 8e confident in the mathematical kil you need to use, such as arithmetic algebraic statistical, estimation and approximation techniques Practise te sis to build confidence + Develop plano sole aprobiem Critically analyse the solution obtained Reflect onthe problem-solving process andthe solution obtained, and make refinements if necessary. + Repeat the process unt you ae happy with the outcome. Present and explain the solution tothe given engineering problem 357TE] Getting ready for assessment How I got started First | collected all my notes on this topic and put them into a folder. | decided to divide my work into sub- topics because | felt it would be easier to revise them individually. | used textbooks and the internet to identify ‘worked examples of typical questions to help revise the information. | started with problems that used the main skills, such as identifying arithmetic and geometric progressions. Then I worked on more complex ones about solving engineering problems to try to achieve all the criteria, How I brought it all together > I went through the worked examples carefully, writing ‘out the solutions myself. > I then tried answering the same questions myself without looking atthe example. > Ithen changed the numbers slightly and tried again Until was confident in solving the problems. > When | was more confident | used questions from other textbooks and the internet. Further Engineering Mathematics Abbie is working towards @ BTEC National in Engineering. She was revising for a time-constrained assignment for Learning aim A. She knew that in the assignment she would have to solve engineering problems using the techniques specified in the Learning air. This was her experience. What I learned from the experience I was pretty sure that I knew how to answer the questions, but | was worried that | would not understand them. | think it helped to use questions from different places for practice because they did not all use the same ‘words, so | got used to having to work out what to do. [ound the questions in textbooks useful because they gave the answers atthe back | ead through the questions carefully before starting to answer them. I worked out how long to spend on each ‘question, so that | would have time to check through for any mistakes. | had planned to answer the questions in a different order from the way they were given, but in the ‘end | did not need to. Doing lots of practice really helped. Think about it » Have you identified what topics you need to revise? > Do you know which problems are routine and which are non-routine? > Have you planned your time? Dorit spend too ong on any one problem