0% found this document useful (0 votes)
20 views33 pagesLec17 Cache 3
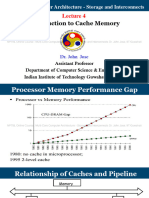
The document discusses cache memory organization and design, focusing on examples of direct-mapped, associative, and set-associative cache mapping techniques. It includes performance comparisons and calculations for cache size requirements based on different configurations. The content is aimed at enhancing understanding of cache efficiency and memory access patterns in computer organization.
Uploaded by
2105019Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
20 views33 pagesLec17 Cache 3
The document discusses cache memory organization and design, focusing on examples of direct-mapped, associative, and set-associative cache mapping techniques. It includes performance comparisons and calculations for cache size requirements based on different configurations. The content is aimed at enhancing understanding of cache efficiency and memory access patterns in computer organization.
Uploaded by
2105019Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 33