A Characterization of the Cantor Function
Author(s): Donald R. Chalice
Source: The American Mathematical Monthly, Vol. 98, No. 3 (Mar., 1991), pp. 255-258
Published by: Mathematical Association of America
Stable URL: http://www.jstor.org/stable/2325032
Accessed: 03-11-2015 05:14 UTC
Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at http://www.jstor.org/page/
info/about/policies/terms.jsp
JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content
in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship.
For more information about JSTOR, please contact support@jstor.org.
Mathematical Association of America is collaborating with JSTOR to digitize, preserve and extend access to The American
Mathematical Monthly.
http://www.jstor.org
This content downloaded from 131.215.225.9 on Tue, 03 Nov 2015 05:14:13 UTC
All use subject to JSTOR Terms and Conditions
�1991] THE TEACHING OF MATHEMATICS 255
"digits"are needed to make T look whole. Anotherexample: T is disconnected,
althoughone cannotreallytell fromthe image-a proofis needed. The fourupper
rightblobs can be separated fromthe fourbottomleftones by a stripthatcan be
physicallymeasuredand seen to be greaterthan 1/50. The modulusof b is smaller
than 0.64, so withthe powers greaterthan 13 a gap wider than 0.6414/(1 - 0.64)
(which is well under 1/50) cannot be bridged. Therefore Tg is indeed discon-
nected.
The set of those b forwhich T is connectedis describedin [3], where,among
otherthings,it is proventhat T is connectedif lbI > 11/2. Amnong the T s shown
in FIGURES 1-10, only T9 and TM are disconnected.
8. Miscellaneous. A lot of thingsare leftto be explored.When T is connected
and simplyconnected (see FIGS. 7 and 8), is the boundaryof fractaldimension
greaterthan 1 (as it seems)? Is that boundarythe image of a continuous
strictly
map from[0, 1] in fR2(as it seems)? Whydoes T5 have T5-like eggs inside it (dark
gray)?
I triedto replace C by the algebrawith(a, b) *(c, d) = (ac + bd, ad + bc), but
got nothingworthshowing.Whynot?
I am gratefulto the refereesformanysuggestions.
Acknowledgement.
REFERENCES
1. D. E. Knuth,The Art of ComputerProgramming, volume 2, SeminumericalAlgorithms,Addison-
Wesley,Reading, Mass., 1981.
2. J. Dieudonne, Fondementsde l'AnalyseModerne, Vol. 1, Gauthier-Villars, Paris, 1965.
3. M. Barnsley,Fractals Everywhere,San Diego, Academic Press, 1988
4. W. J. Gilbert,Fractal geometryderivedfromcomplexbases, Math. Intelligencer, 4 (1982) 78-86
Indiana Univ.Math.J.,30 (1981) 713-747.
5. J. E. Hutchinson,Fractals and self-similarity,
A Characterizationofthe CantorFunction
DONALD R. CHALICE
DepartmentofMathematics,WesternWashington
University,
Bellingham,WA98225
This note presentsa characterization of the Cantorfunctionthatmightbe used
as an alternativeor additionto the developmentusuallypresentedin real analysis
courses.It mayalso be utilizedto give a shortprogramin Mathematicathateasily
generatesthe Cantor functionand other similarfunctionswhichwe call "devil's
staircases"(see [4]).
THEOREM. Any real-valuedfunctionF(x) on [0, 1] that is monotoneincreasing
and satisfies(a) F(O) = 0, (b) F(x/3) = F(x)/2, and (c) F(1 - x) = 1 - F(x), is
theCantorfunction.
Before presentingthe proof, recall (see [1]) that if we consider the closed
interval[0, 1] and removethe open middle third,(1/3, 2/3), and nextremovethe
open middlethirds(1/9, 2/9) and (7/9, 8/9) of the two remainingintervals,and
then remove the open middle thirdsof the remainingfour intervalsand so on,
indefinitely,what remainsis the Cantorset C. Alternatively,x is in C iffx has a
base-3 expansionconsistingonlyof the digits0 and 2.
This content downloaded from 131.215.225.9 on Tue, 03 Nov 2015 05:14:13 UTC
All use subject to JSTOR Terms and Conditions
�256 DONALD R. CHALICE [March
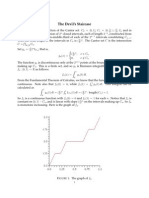
The CantorfunctionG(x) may be definedas follows.First defineit on C: if
x = i22 3-'f, then G(x) = i2-'. The function G is monotone and has the
same values at the endpoints of each removed interval,so G extends to a
continuousfunctionon [0, 1] (see FIGURE 3(a)).
On [1/3, 2/3], G has value 1/2, on [1/9, 2/9] and [7/9, 8/9], G has values
1/4 and 3/4, respectively.On the intervals[1/27, 2/27], [7/27, 8/27], [19/27,
20/27], and [25/27, 26/27], the values of G are 1/8, 3/8, 5/8, and 7/8,
respectively.Since G is (locally) constanton some neighborhoodof everypointin
[0, 11\ C, G'(x) = 0 almosteverywhereon [0, 1]. (See [1] or [3].)
Proof of the theorem.First observe that in constructingthe Cantor set, the
removed intervals(in base 3) are as given in TABLE 1. The endpointsof any
removedintervalat the nth stage are foundby eithermultiplying those fromthe
by .1 and adding
previousstageby .1 (base 3), or bymultiplying .2.
TABLE 1
Step Values of G Removed Intervals(closures)
1 1/2 [.1,.2]
2 1/4, 3/4 [.01,.02],[.21,.22]
3 1/8, 3/8 [.001,.002],[.021,.022],
5/8, 7/8 [.201,.202],[.221,.222]
4 1/16, 3/16 [.0001,.0002],[.0021,.0022],
5/16, 7/16 [.0201,.0202],[.0221,.0222]
9/16, 11/16 [.2001,.2002],[.2021,.2022],
13/16, 15/16 [.2201,.2202],[.2221,.2222],etc.
Alternatively,any permutationof n - 1 Os and 2s after the ternarypoint
followedby a 1 or a 2 givesa removedintervalat the nth stage.
Recursion is now used to characterizeF: By (a) and (c), F(1) = 1, so F(.1) =
1/2. By (b) and (c), F(.2) = 1 - F(.1) = 1/2; (b) implies F(.01) = F(.02) = 1/4
and (c) implies F(.22) = F(.21) = 3/4; (b) then yields the correctvalues of 1/8,
3/8 on the firststwo intervalsat stage 3, while (c) yieldsthe value F(.201) = 1 -
F(.022) = 5/8. It followsby inductionthat F and G agree on a dense subset of
[0, 1]. Since F is monotone increasingand has no jump discontinuities,F is
continuous(because any discontinuityof a monotone functionis a jump; see
[1, p. 129]). Thus since F is continuousand agrees withthe Cantor functionon a
dense set, F is the Cantor function,and the proofis complete.
As an alternativeproofof continuity, F maybe exhibitedas a uniformlimitof a
sequence of monotone increasingstep functions{s,1} on [0, 1] with the jumps
convergingto 0. For example,define
{0 if x <.1
S1(x) = /2 if.1 < x < .2
\1 if.2 <x
define
and inductively,
Sn 1(3x)/2 if x < .1
sn(x) = /2 if.1 Ax < .2
1 - sn( -x) if .2 < x
(assuming sn as definedon the firstline). The continuityof F is then a conse-
quence of the followinglemma,whichmaybe of independentinterest.
This content downloaded from 131.215.225.9 on Tue, 03 Nov 2015 05:14:13 UTC
All use subject to JSTOR Terms and Conditions
�1991] THE TEACHING OF MATHEMATICS 257
I ( I
Figure l(a) Graph of s1.
1 --1 (-0
'> ) l l I *4 l I~~~~~~~~~~~~~~~~~~~~~~~~~
l
11 1
Figure l(b) Graph of S2* Figure l(c) Graph of s3.
LEMMA.Let {snJbe a Cauchy sequence in uniformnorm of stepfunctionson
witha finitenumberof jumps such that theheightsof thejumpsfor Sn
[0, 1], each
convergeuniformlyto 0. Thens,nconvergesuniformlyto a continuousfunctionF on
[0,1].
Proof. Pick x in [0, 1] and E > 0. There existsan integerN such that n, m > N
impliesIsn(x) - sm(x)l < E/4 forall x in [0, 1], and so thatthejumps of Sn are all
less than E/4. Now any sn is uniformly continuouson each intervalon whichthere
is not a jump,so we can pick ( so thatIx - yI < 8 impliesIsN(X) - SN(Y)I < 2e/4.
Hence, Ix - yl < 8 implies IF(x) - F(y)l < IF(x) - sN(X)I + ISN(X) - SN(Y)l +
ISN(y) - F(y)l < E. Thus F is continuous. QED
Since n < m impliesIsn(x) - Sm(X)l < ISn- 1(y) - Sm-1(y)I/2 where y is one of
3x or 1 - 3x, it thenfollowsinductivelythat Isn(x) - Sm(X)l< 1/2n when n < m.
Thus {snj is uniformly Cauchy and the continuityof F followsfromthe lemma.
Note also thatF maybe generatedbya geometricalgorithm, wherewe beginby
definingF(x) = 1/2 on the interval[.1,.2] and F(O) = 0, F(1) = 1, and where at
each stage of the algorithmwe shrinkthe x axis by a factorof 1/3 and the y axis
by a factorof 1/2 and then flipthe resultantgraphacross the line x = 1/2, and
then again across the line y = 1/2. We see F as comingmore into focus at each
stage.
The precedingcharacterization was used (togetherwiththe recursivefeatureof
Mathematica)to generate FIGURES 3(a)-(b) (programmedby Gerald Harnett).
Other "devil's staircases" were obtained by taking any p > 0 and changing
condition(c) to (c): F(1 - x) = 1 - pF(x), forx < 1/3 and condition(b) to (b ):
F(x/3) = F(x)/(p + 1). These generalizationsarise as the cumulativedistribu-
tion functionsof some of the probabilitymeasures invariantunder the "inverted
This content downloaded from 131.215.225.9 on Tue, 03 Nov 2015 05:14:13 UTC
All use subject to JSTOR Terms and Conditions
�258 DONALD R. CHALICE
I 11
Figure2(a). Figure2(b)
Shrink2(a) and superimposeon 2(a).
I~~~~~~~~~
T I
Figure2(c) Figure2(d)
Double flip2(b) and superimposeon 2(b). Shrink2(c) and superimposeon 2(c).
1. -- )0.75
0.75
0.5
0.5
-_ )0.25
0.25
0.25 0.5 0.75 1. 0.25 0.5 0.75 1
The Cantor function(p = 1). The Cantor function(p = 2).
FIG. 3a FIG. 3b
V" transformation discussedby Mandelbrot(see [2,4]). Finally,by lettingp take
on, forexample,the values .01, .1, .3, .5, 1, 4, 10, and 100, one can create a movie
in Mathematicathat shows the Cantor function"stressed" by the varyingof the
parameterp (see FIGURE 3).
REFERENCES
1. R. P. Boas, Jr.,A Primerof Real Functions,Carus MathematicalMonographs,No. 13, Wiley,
Rahway,New Jersey,1960.
2. D. R. Chalice, Devil's staircasesinvariantunder the invertedV function,to appear.
3. B. R. Gelbaum and J. M. H. Olmsted,Counterexamplesin Analysis,Holden-Day, San Francisco,
1964.
4. B. B. Mandelbrot,The Fractal Geometryof Nature,W. H. Freeman,New York, 1983.
This content downloaded from 131.215.225.9 on Tue, 03 Nov 2015 05:14:13 UTC
All use subject to JSTOR Terms and Conditions