The Cantor set and the Devil’s staircase

Manuela Girotti

MATH 3441 Real Analysis I

In these notes we will prove a few properties of the Cantor set and we will construct a
pathological function D : [0, 1] → [0, 1] (the “Devil’s staircase”) that is continuous everywhere,
whose derivative is zero almost everywhere, but it somehow magically rises from 0 to 1.
The section about the Devil’s staircase will be more of a collection of facts with very few
proofs, than a thorough exposition. We will explore the topic more in details in our upcoming
course Real Analysis II!

1 The Cantor set C

The (standard) Cantor set is the set C ⊆ [0, 1] constructed as follows.
We start with the full interval F0 = [0, 1]. Divide F0 into three equal parts and let I1 be the
open middle third of F0 , that is I1 = ( 13 , 23 ), and define

F1 = F0 \ I1 = 0, 13 ∪ 23 , 1 .
   

Let I2 and I3 be the open middle thirds of the two component intervals of F1 , i.e. I2 = ( 19 , 29 )
and I3 = ( 97 , 89 ), and define
       
1 2 3 6 7 8
F2 = F1 \ (I2 ∪ I3 ) = 0, ∪ , ∪ , ∪ ,1 .
9 9 9 9 9 9

Continue the construction iteratively: having constructed the set Fn , which is the disjoint union
of 2n closed intervals each of length 31n , let I2n , I2n +1 , . . . , I2n+1 −1 be the open middle thirds to
of these 2n component intervals and define

Fn+1 = Fn \ (I2n ∪ I2n +1 ∪ . . . ∪ I2n+1 −1 ) .

See the figure below to get an idea of how these sets look like.

Then, the Cantor set is

∞
\
C= Fn .
n=1

The first straightforward properties of the Cantor set are the following.

1
Proposition 1. The Cantor set is closed and nowhere dense.
Proof. For any n ∈ N, the set Fn is a finite union of closed intervals. Therefore, C is closed
because intersection of a family of closed sets. Notice that this will additionally imply that C is
compact (as C ⊂ [0, 1]).
Now, since C = C, we simply need to prove that C has empty interior: C ◦ = ∅. Assume by
contradiction that C ◦ 6= ∅, i.e. there exists an interior point x0 ∈ C: therefore, ∃  > 0 such that
(x0 − , x0 + ) ⊂ C. Let N ∈ N such that 31N < 2. By construction,
∞
\
C= Fn ⊂ FN
n=1

and FN is the union of 2N intervals, each of length 31N which is strictly less than the length of
the interval (x0 − , x0 + ). Thus, the contradiction.
A little more work is required to prove the following property.
Proposition 2. The Cantor set is uncountable.
Let us first consider an equivalent representation of the Cantor set that will help us in the
proof. We start by noticing that every x ∈ [0, 1] admits at most two representations in base 3
(ternary expansion):
∞
X dj
x = 0.d1 d2 d3 . . . =
3j
j=1
with dj ∈ {0, 1, 2} (the endpoint x = 1 has representation 1 = 0.22222 . . .).
The only cases where x ∈ [0, 1] may admit two equivalent expansions arise when x ∈ Q and
its denominator is a multiple of 3: for example, 13 = 0.10000 . . . = 0.02222 . . .. In these (at most
countably many) cases we have two representations for x = 0.d1 d2 d3 . . . = 0.c1 c2 c3 . . .), however
they can be easily identified: let N := min{j ∈ N | dj 6= cj } and (w.l.o.g.) assume dN < cN ;
then, necessarily cN = dN + 1 and cN +1 = cN +1 = . . . = 0 and dN +1 = dN +2 = . . . = 2 (in
particular, either cN = 1 or dN = 1). Therefore among those two ternary expansion, there is
only one which doesn’t contain 1’s.
Within this setting, the Cantor set can be represented as
C = {x = 0.d2 d2 d3 . . . | dj ∈ {0, 2} ∀ j ∈ N} .
Indeed, starting from the first “mid-pinch” I1 we have that the endpoints
1 2
= 0.10000 . . . = 0.02222 . . . and = 0.20000 . . . = 0.12222 . . .
3 3
and any other point x ∈ I1 has base-3 representation of the form x = 0.1d2 d3 d4 d5 . . . where the
sequence d2 d3 d4 d5 . . . is strictly between 0000 . . . and 2222 . . ..
Therefore, all points x ∈ F1 = [0, 1] \ I1 have base-3 representation of the form x =
0.0d2 d3 d4 d5 . . . or x = 0.2d2 d3 d4 d5 . . .. At the next step, similarly, the “mid-pinch” removes
numbers of the form x = 0.01d3 d4 d5 . . . and x = 0.21d3 d4 d5 . . ., therefore points x ∈ F2 =
F1 \ (I2 ∪ I3 ) have a base-3 representation whose first two digits are restricted from being equal
to 1. Continuing on in the construction of the sets Fn , we can see that the points in Fn have a
base-3 expansion whose n-th digit is not equal to 1.
We are now ready to prove Proposition 2.
Proof. Assume that C is countable and collect all of its points in an infinite table:
x1 = 0.d11 d12 d13 d14 d15 . . .
x2 = 0.d21 d22 d23 d24 d25 . . .
x3 = 0.d31 d32 d33 d34 d35 . . .
x1 = 0.d41 d42 d43 d44 d45 . . .
..
.

2
f1 (x) f2 (x) f3 (x) f4 (x)

Figure 1: The first functions in the sequence {fn } converging to the Devil’s staircase D.

By using Cantor diagonalization trick (seen in class), we can easily construct a new point x̄ ∈ C,
which has not being accounted for in the table, by considering all the “diagonal” digits djj in
the table above and replacing any 0 with 2 and viceversa. Thus, the contradiction.

2 The Devil’s staircase

The formal definition of the Devil’s staircase function D is the following. Recall the ternary
representation of a point x ∈ [0, 1]:
∞ (x)
X dj (x)
x= , with dj ∈ {0, 1, 2} ;
3j
j=1

(x)
denote by Nx the smallest index j such that dj = 1, if it exists, otherwise Nx = ∞. Then, the
Cantor function is the following
Nx −1 (x)
1 1 X dj
D(x) := +
2Nx 2 2j
j=1

Remark 3. Notice that D is well defined, i.e. its value is independent on the choice of the
base-3 expansion in the cases where x admits two of them.

An alternative way to define such a function (and an easier way to visualize it) is through an
iterative construction. We consider the following a sequence of continuous functions {fn }n∈N ∈
Fb ([0, 1]; [0, 1]) ∩ C 0 ([0, 1]): let
f1 (x) = x
and ∀ n ∈ N we have

1
 2 fn (x)
 x ∈ [0, 13 )
1
fn+1 (x) = 2 x ∈ [ 13 , 23 ]

1
2 + 12 fn (3x − 2) x ∈ ( 23 , 1]

By induction, it is possible to prove that fn is indeed a continuous function on [0, 1], for
every n ∈ N.

Proposition 4. The sequence of functions {fn } defined above converges uniformly to the Devil’s
staircase:
kfn − Dk∞ → 0 , as n → ∞ .

Proof. As a first step, by using again the ternary representation of points in [0, 1], we notice
that fn (x) converges pointwise to D(x) (why?). Th uniform convergence follows by noticing
that the sequence of functions {fn } is Cauchy.

3
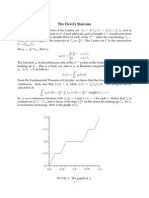
 Figure 2: The Devil’s staircase D.

Indeed, consider the quantity

1 1
kfn+1 − fn k∞ = sup |fn+1 (x) − fn (x)| = sup |fn (x) − fn−1 (x)| = kfn − fn−1 k∞ , ∀ n ≥ 1;
x∈[0,1] 2 x∈[0,1] 2

therefore,
1 1
kfn+1 − fn k∞ ≤ kfn − fn−1 k∞ ≤ . . . ≤ n kf2 − f1 k∞ .
2 2 | {z }
= 16

Recall now the following property (see Homework 6): given a sequence {xn } in a metric space
(X, d), if there exists a sequence {γn }∞ n=1 ⊂ [0, +∞) such that

(ii) ∞
P
(i) d(xn , xn+1 ) ≤ γn , ∀ n ≥ 1 and n=1 γn < ∞ ,

then {xn } is a Cauchy sequence.

1
∈ (0, +∞ ∀ n ≥ 1 and n γn = 31 n 2n+1
P P 1
In our case we have γn = 32n+1 < +∞ (geometric
series with ration q = 12 < 1). Therefore our sequence of functions {fn } ⊂ Fb ([0, 1]; [0, 1]) ∩
C 0 ([0, 1]) is a Cauchy sequence, therefore it is convergent (recall that (Fb ([0, 1]; [0, 1]), k · k∞ ) is
a Banach space).

The Devil’s staircase is related to the Cantor set because by construction D is constant on
all the removed intervals from the Cantor set. For example: D(x) = 21 for x ∈ I1 = ( 31 , 23 ),
D(x) = 14 for x ∈ I2 = ( 91 , 29 ) and D(x) = 34 for x ∈ I3 = ( 79 , 89 ), and so on.
Further properties are listed (and partly proven) in the Proposition below:
Proposition 5. The Devil’s staircase D : [0, 1] → [0, 1] satisfies the following properties:
1. D is (uniformly) continuous and monotone increasing.
2. D has derivative equal to zero almost everywhere.
(the precise formulation is that D 0 (x) = 0 ∀ x ∈ [0, 1] \ C and C has measure zero).
3. The arc length of the graph of D is equal to 2.
Proof. (partial – tune in for Real Analysis II for more!
D is continuous, since uniform limit of continuous functions. It is additionally uniformly
continuous because it is defined on the compact set [0, 1]. Additionally, ∀ n ∈ N we have that
fn (0) = 0, fn (1) = 1 and fn (x) ≤ fn (y) ∀ x, y ∈ [0, 1], x ≤ y, therefore such properties still hold
in the limit: D(0) = 0, D(1) = 1 and D(x) ≤ D(y) ∀ x < y.