0% found this document useful (0 votes)
24 views7 pagesSB Pages 27-33 (Answers)
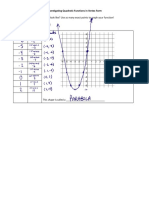
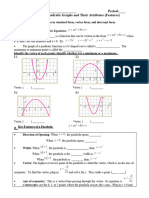
The document outlines key standards and learning targets for understanding quadratic functions, including their graphing, properties, and relationships between coefficients. It provides exploration questions, diagnostic assessments, and problem-solving scenarios to enhance comprehension of quadratic equations. Additionally, it emphasizes the importance of identifying features such as the vertex, axis of symmetry, and intercepts in various forms of quadratic functions.
Uploaded by
elochessmaster2000Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
24 views7 pagesSB Pages 27-33 (Answers)
The document outlines key standards and learning targets for understanding quadratic functions, including their graphing, properties, and relationships between coefficients. It provides exploration questions, diagnostic assessments, and problem-solving scenarios to enhance comprehension of quadratic equations. Additionally, it emphasizes the importance of identifying features such as the vertex, axis of symmetry, and intercepts in various forms of quadratic functions.
Uploaded by
elochessmaster2000Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 7