0% found this document useful (0 votes)
30 views4 pagesRimon Numerical 10
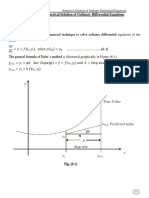
The document outlines an experiment focused on solving first-order ordinary differential equations (ODEs) using various numerical methods, including Euler’s Method, Heun’s Method, Modified Euler’s Method, and Runge-Kutta 4th Order Method. It discusses the implementation of these methods, their accuracy, and the comparison of their results against the exact solution. The conclusion highlights that while Euler’s method is the simplest, the Runge-Kutta 4th Order Method offers the best accuracy and stability for solving ODEs.
Uploaded by
www.almominhossain9Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
30 views4 pagesRimon Numerical 10
The document outlines an experiment focused on solving first-order ordinary differential equations (ODEs) using various numerical methods, including Euler’s Method, Heun’s Method, Modified Euler’s Method, and Runge-Kutta 4th Order Method. It discusses the implementation of these methods, their accuracy, and the comparison of their results against the exact solution. The conclusion highlights that while Euler’s method is the simplest, the Runge-Kutta 4th Order Method offers the best accuracy and stability for solving ODEs.
Uploaded by
www.almominhossain9Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 4