0% found this document useful (0 votes)
74 views5 pagesHigh School Olympic Math Contest Practice (4) Part A
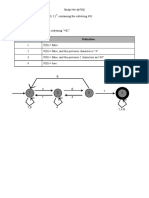
The document contains a series of math problems from a High School Olympic Math Contest practice, covering various topics such as geometry, algebra, and number theory. Each problem presents multiple-choice answers, requiring students to apply mathematical concepts to find solutions. The problems range in difficulty and are designed to challenge students' problem-solving skills.
Uploaded by
Jiusong ZhaoCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
74 views5 pagesHigh School Olympic Math Contest Practice (4) Part A
The document contains a series of math problems from a High School Olympic Math Contest practice, covering various topics such as geometry, algebra, and number theory. Each problem presents multiple-choice answers, requiring students to apply mathematical concepts to find solutions. The problems range in difficulty and are designed to challenge students' problem-solving skills.
Uploaded by
Jiusong ZhaoCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 5