0% found this document useful (0 votes)
15 views29 pagesAlgebra 10 Graphs of Functions
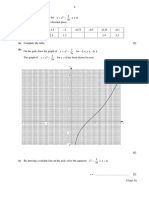
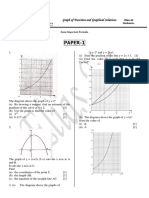
The document contains a series of mathematical problems related to graphing functions, solving equations, and analyzing data tables. It includes tasks such as finding function values, sketching graphs, and determining intersections of curves. The document is structured with numbered sections, each containing specific questions and instructions for completion.
Uploaded by
Tety SuryaniCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
15 views29 pagesAlgebra 10 Graphs of Functions
The document contains a series of mathematical problems related to graphing functions, solving equations, and analyzing data tables. It includes tasks such as finding function values, sketching graphs, and determining intersections of curves. The document is structured with numbered sections, each containing specific questions and instructions for completion.
Uploaded by
Tety SuryaniCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 29