0% found this document useful (0 votes)
13 views9 pagesLab 1 Robotics
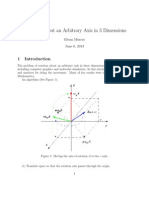
The document outlines the assessment rubrics for a Biomedical Robotics Lab course, focusing on students' ability to use software tools for kinematic modeling and simulation of robotic manipulators. It details performance indicators ranging from exemplary to unsatisfactory in conducting experiments and simulations. Additionally, it provides an overview of transformation matrices, rotation matrices, and tasks related to MATLAB programming for robotic applications.
Uploaded by
AminaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
13 views9 pagesLab 1 Robotics
The document outlines the assessment rubrics for a Biomedical Robotics Lab course, focusing on students' ability to use software tools for kinematic modeling and simulation of robotic manipulators. It details performance indicators ranging from exemplary to unsatisfactory in conducting experiments and simulations. Additionally, it provides an overview of transformation matrices, rotation matrices, and tasks related to MATLAB programming for robotic applications.
Uploaded by
AminaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 9