0% found this document useful (0 votes)
28 views11 pagesUnit-5 (B) Vector Calculus Lecture Notes
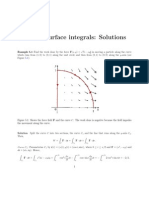
The document provides lecture notes on Vector Calculus, specifically focusing on line integrals and surface integrals. It defines line integrals as a generalization of definite integrals along a curve in space and includes examples of evaluating line integrals and calculating work done by a force field. Additionally, it explains surface integrals and provides methods for evaluating them over specified surfaces.
Uploaded by
studywork700Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
28 views11 pagesUnit-5 (B) Vector Calculus Lecture Notes
The document provides lecture notes on Vector Calculus, specifically focusing on line integrals and surface integrals. It defines line integrals as a generalization of definite integrals along a curve in space and includes examples of evaluating line integrals and calculating work done by a force field. Additionally, it explains surface integrals and provides methods for evaluating them over specified surfaces.
Uploaded by
studywork700Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 11