50% found this document useful (2 votes)
5K views11 pagesChapter 6
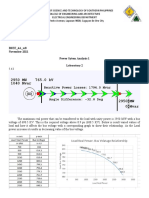
The document contains 7 multi-part engineering problems involving calculations related to internal combustion engines. The problems cover topics like ideal thermal efficiency, mean effective pressure, engine power output, oil API rating, fuel consumption rates, excess air in combustion, and brake mean effective pressure. Step-by-step solutions and calculations are provided for each problem.
Uploaded by
Jigs SanaresCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
50% found this document useful (2 votes)
5K views11 pagesChapter 6
The document contains 7 multi-part engineering problems involving calculations related to internal combustion engines. The problems cover topics like ideal thermal efficiency, mean effective pressure, engine power output, oil API rating, fuel consumption rates, excess air in combustion, and brake mean effective pressure. Step-by-step solutions and calculations are provided for each problem.
Uploaded by
Jigs SanaresCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 11